Oscilações – Exercícios

Fuja do Nabo: Física II – P2 – 2014 – Rogério Motisuki
Oscilações – Exercícios
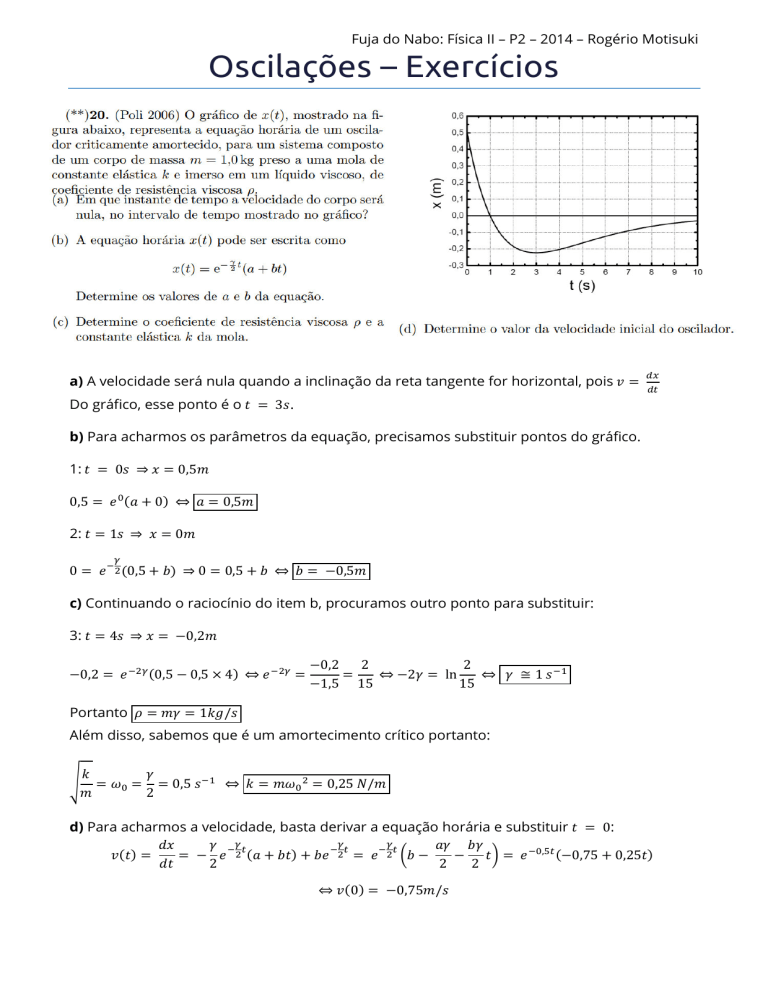
a) A velocidade será nula quando a inclinação da reta tangente for horizontal, pois
Do gráfico, esse ponto é o = 3 .
=
b) Para acharmos os parâmetros da equação, precisamos substituir pontos do gráfico.
1: = 0 ⇒
0,5 = = 0,5
+ 0 ⇔
2: = 1 ⇒ = 0
0 =
0,5 +
= 0,5
⇒ 0 = 0,5 + ⇔
= −0,5
c) Continuando o raciocínio do item b, procuramos outro ponto para substituir:
3: = 4 ⇒
= −0,2
−0,2 = 0,5 − 0,5 × 4 ⇔
Portanto % =
= 1&'/
=
−0,2
2 2 = ⇔ −2 = ln ⇔ ≅ 1
−1,5 15
15
$
Além disso, sabemos que é um amortecimento crítico portanto:
)
&
=* =
2
= 0,5
$
⇔ & =
*
= 0,25+/
d) Para acharmos a velocidade, basta derivar a equação horária e substituir = 0:
,
,/
=
=−
+
+
=
- − −
. =
−0,75 + 0,25 ,
2
2
2
⇔
0 = −0,75 /
a) Do gráfico, 1 = 6
b) Atenção: não é um gráfico de posição.
= −* 3 cos *
A aceleração é dada por
+ 7
Portanto, o valor máximo do gráfico é igual a * 3, onde * = 10 = * 3 ⇔ 3 = 10
1
90
=
>
4;² ;²
8
9
8
:
= :
c) Já temos a amplitude e a frequência, só precisamos achar a fase inicial. Como o gráfico que
temos é de aceleração, precisamos substituir pontos na expressão certa para achar a fase.
1: = 0 ⇒
=5
1 2;
4;
5 = −10 cos 7 ⇔ cos 7 = − ⇔ 7 = ?@
2
3
3
Para decidir entre essas duas fases, temos duas alternativas: substituir um segundo ponto do
gráfico, ou analisar a tendência do gráfico.
Analisamos quando
= 0 e obtivemos duas possibilidades. Olhando no gráfico vemos que o
gráfico atinge um ponto de máximo logo após = 0, portanto a fase inicial precisa ser
Se a fase inicial fosse
Logo:
= 3 cos *
A8
,
:
8
.
:
o gráfico atingiria um ponto de zero em vez de um ponto de máximo.
B
8
+ 7 = 8² cos C : +
d) Derivando e substituindo:
8
D >
:
= −* 3 sen *
+ 7 = −
:
8
8
FC : D = −
: √:
>
8
/
e) É mais fácil calcular a energia potencial máxima do sistema, quando a posição atinge a
amplitude, a energia cinética será zero, portanto:
Precisamos ainda achar a constante da mola: HJ = * = : ⇔ & =
Logo K = IL²
$
= ×
8²
×
:
,B
C 8² D =
, M
N
8²
I
8
* =
8²
:
a) Para achar equações diferenciais, precisamos usar o torque ou a força. Como é um
problema angular, é muito mais fácil usar o torque.
Definindo como positivo o sentido antihorário, o torque exercido pela força peso na barra é:
R
O = −P'. FS.
3
O momento de inércia em torno daquele ponto O, é dado pelo teorema dos eixos paralelos:
PR²
R
7
TU = TVW + P,² =
+ P- .² =
PR²
12
3
36
Portanto, temos:
R
7
, S , S
12'
12'
FS = PR ⇔
=−
FS ≅ −
S
3
36
,
,
7R
7R
b) A partir da equação achada no item a, segue que:
O = TX ⇔ −P'
* ² =
12' 12'
⇔ * = )
7R
7R
8
M\
]
Portanto: 1Y = Z = 2;H$
[
c) A solução é da forma: S
= 3 cos *
+7
Temos duas informações para substituir e achar os outros parâmetros o ângulo inicial é S e a
velocidade inicial é nula.
3>? 7 = S
3 =S
S = 3>? 7
⇔ ^
⇔^
⇒ S
^
7=0
F 7 =0
0 = −* 3 F 7
12'
= S cos _)
`
7R
d) A pergunta é esquisita, pois como não há atrito, a energia mecânica é constante para
qualquer ângulo.
É mais fácil calcular a energia mecânica quando ou a cinética, ou a potencial for zero. Neste
caso, como não temos informações de velocidade sem precisar calcular, o mais simples é
calcular a energia potencial no ponto de amplitude máxima:
Nesse ponto, a energia potencial gravitacional é:
K = P'ℎ, onde ℎ é a distância vertical do centro de massa até a altura de referência. A
referência é tomada de forma que a mínima energia gravitacional durante o movimento seja 0.
Ou seja, a altura de referência é a mínima atingida pelo centro de massa, quando o ângulo é 0.
Quando o ângulo for a amplitude, S , a altura ℎ será:
R
R
R
ℎ = − - cos S . = 1 − cos S
3
3
3
²
Para ângulos pequenos, cos = 1 − , portanto:
R
S
R
ℎ ≅ b1 − 1 + c = S ²
3
2
6
Assim, a energia mecânica da oscilação é:
1
K = P'RS ²
6
e) Basta usar o mesmo raciocínio utilizado no item b, porém trocando o momento de inércia e
o torque.
O torque agora é:
R
O = −P'. FS.
2
Usando o teorema dos eixos paralelos:
PR²
R
PR²
+ P- .² =
Td = TVW + P,² = 12
2
3
Logo, temos:
O = TX ⇔ −P'
R
2
1
, S , S
3'
FS = PR ⇔
=−
3
,
,
2R
Assim, da equação diferencial tiramos: * ² = 8
\
Portanto: 1d = Z = 2;H:]
[
FS ≅ −
:] ⇔ *
\
Usando o resultado do item b, calculamos a razão:
=H
3'
S
2R
:]
\
2R
2;H3'
1d
2 12
8
=
=) ×
=)
1Y
3 7
7
7R
2;H12'
O que é mais importante:
Achar a equação diferencial
Use seus conhecimentos de mecânica para marcar forças no desenho. Agora decida entre usar
torque resultante ou força resultante:
Se você quiser achar:
ângulo S
posição
⇒ f O = TX
⇒ f g = P
Identificar qual solução usar
4 possibilidades:
MHS:
Amortecimento subcrítico * > :
=3
Amortecimento crítico * = :
= 3 cos *
cos * + 7 ?F, * = )*
=
Amortecimento supercrítico * < :
=
+7
k3
l
+i
−
4
3+i
l
m?F, n = )
Achar os outros parâmetros da equação
4
−*
Para achar 3, i 7 é possível somente com informações do enunciado ou de um gráfico,
substituindo nas equações e resolvendo.
Para achar * pode ser necessário usar informações de um gráfico também, mas há a
possibilidade de serem obtidas através da montagem da equação diferencial. Essa montagem
nem sempre é necessária, visto que:
* : Frequência angular que o sistema oscilaria caso não tivesse atrito (caso MHS).
= J , ?F, %é?>? rs>s F
p
, g = −%
Calcular a energia da oscilação
Numa oscilação: K = Ktuv + KwY
Geralmente é mais fácil calcular a energia total num ponto onde uma delas é zero, e na
maioria dos casos é mais fácil quando é a cinética que é zero.
Lembre que a energia cinética é nula nos pontos de amplitude.
Calcular outras grandezas do problema físico
Período T e frequência f: 1 = =
$
x
8
Z