2.4 TRANSFORMAÇÕES LINEARES PLANAS

2.4 TRANSFORMAÇÕES LINEARES PLANAS
2.4.1 Reflexão
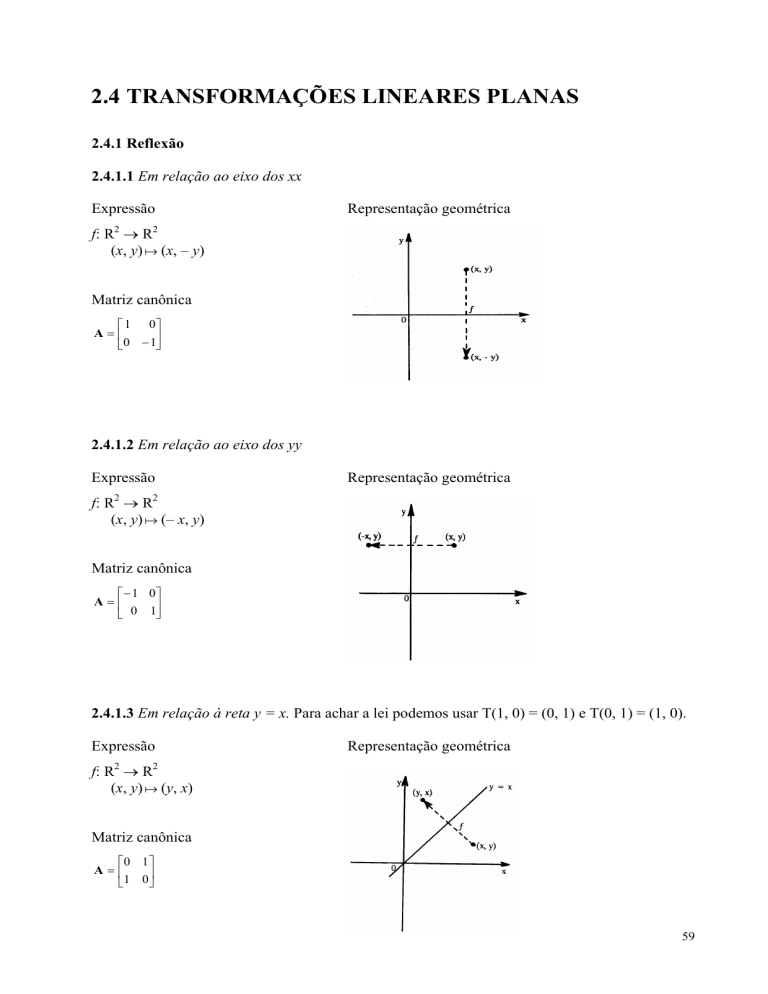
2.4.1.1 Em relação ao eixo dos xx
Expressão
Representação geométrica
f: R2 → R2
(x, y) 6 (x, – y)
Matriz canônica
⎡ 1 0⎤
A=⎢
⎥
⎣0 − 1⎦
2.4.1.2 Em relação ao eixo dos yy
Expressão
Representação geométrica
f: R2 → R2
(x, y) 6 (– x, y)
Matriz canônica
⎡ − 1 0⎤
A=⎢
⎥
⎣ 0 1⎦
2.4.1.3 Em relação à reta y = x. Para achar a lei podemos usar T(1, 0) = (0, 1) e T(0, 1) = (1, 0).
Expressão
Representação geométrica
f: R2 → R2
(x, y) 6 (y, x)
Matriz canônica
⎡0 1 ⎤
A=⎢
⎥
⎣1 0 ⎦
59
2.4.1.4 Em relação à reta y = – x. Podemos achar a lei tomando T(0, 1) = (– 1, 0) e T(1, 0) = (0,
– 1).
Expressão
Representação geométrica
f: R2 → R2
(x, y) 6 (– y, – x)
Matriz canônica
⎡ 0 − 1⎤
A=⎢
⎥
⎣ − 1 0⎦
2.4.2 Projeção
2.4.2.1 sobre o eixo dos xx
Expressão
Representação geométrica
f: R2 → R2
(x, y) 6 (x, 0)
Matriz canônica
⎡1 0⎤
A=⎢
⎥
⎣ 0 0⎦
2.4.2.2 sobre o eixo dos yy
Expressão
Representação geométrica
f: R2 → R2
(x, y) 6 (0, y)
Matriz canônica
⎡ 0 0⎤
A=⎢
⎥
⎣ 0 1⎦
60
2.4.3 Dilatação ou Contração
Seja α um número real não nulo.
2.4.3.1 Na direção do vetor (α ∈ R)
Expressão
Representação geométrica
f: R2 → R2
(x, y) 6 (αx, αy)
Matriz canônica
⎡α 0 ⎤
A=⎢
⎥
⎣ 0 α⎦
2.4.3.2 Na direção do eixo dos xx (horizontal)
Expressão
Representação
geométrica
1
2
para o caso α = 2 e α = .
f: R2 → R2
(x, y) 6 (αx, y)
Matriz canônica
⎡α 0⎤
A=⎢
⎥
⎣ 0 1⎦
2.4.3.3 Na direção do eixo dos yy (vertical)
Expressão
Representação
geométrica
1
2
para o caso α = 2 e α = .
61
f: R2 → R2
(x, y) 6 (x, αy)
Matriz canônica
⎡1 0 ⎤
A=⎢
⎥
⎣0 α ⎦
2.4.4 Cisalhamento
2.4.4.1 Na direção do eixo dos xx
Expressão
Representação geométrica
f: R2 → R2
(x, y) 6 (x + αy, y)
Matriz canônica
⎡1 α ⎤
A=⎢
⎥
⎣0 1 ⎦
2.4.4.2 Na direção do eixo dos yy
Expressão
Representação geométrica
f: R2 → R2
(x, y) 6 (x, αx + y)
Matriz canônica
⎡ 1 0⎤
A=⎢
⎥
⎣α 1⎦
62
2.4.5 Rotação de um ângulo θ no sentido anti-horário
Expressão
Representação geométrica
Rθ: R2 → R2
v 6 Rθ(v)
(x, y) 6 (x', y') = ?
Matriz canônica
⎡cos θ − sen θ⎤
A=⎢
cos θ⎥⎦
⎣sen θ
Observando a representação geométrica, temos que:
Lembremos que:
| v | = | Rθ(v) |;
sen (α + θ) = sen α cos θ + sen θ cos α
y
sen α =
;
| v|
cos (α + θ) = cos α cos θ – sen α sen θ
cos α =
x
;
| v|
Assim,
sen (α + θ) =
y,
| v|
sen α cosθ + sen θ cosα =
cosθ
y
x
y,
+ sen θ
=
| v|
| v| | v|
x sen θ + y cosθ = y ,
cos (α + θ) =
y,
| v|
x,
|v|
cosα cosθ − sen α sen θ =
x,
|v|
x
y
x,
cosθ −
sen θ =
|v|
|v|
|v|
x cosθ − y sen θ = x,
⎡cos θ − sen θ⎤
.
cos θ⎥⎦
⎣sen θ
Então, Rθ (x, y) = (x cos θ – y sen θ, x sen θ + y cos θ ) e [R θ ] = ⎢
2.4.6 Exemplo. Considere o triângulo de vértices A (– 3, 1), B(1, – 3) e C(3, 3) sobre o qual se
aplicam, respectivamente, as seguintes transformações: reflexão em relação ao eixo dos xx e
duplicação dos módulos.
a) Encontrar os vértices A1, B1 e C1 determinados pela primeira transformação e os vértices A2,
B2 e C2 determinados pela segunda transformação.
b) Representar, geometricamente, no mesmo sistema de eixos cartesianos os triângulos ABC,
A1B1C1 e A2B2C2.
Solução.
a)
• Vamos designar por f1 e f2 a primeira e segunda transformação, respectivamente:
63
f1: reflexão em torno do eixo dos xx ⇒ (x, y) 6 (x, – y);
f2: duplicação dos módulos ⇒ (x, y) 6 (2x, 2y)
Para encontrarmos os vértices A1, B1 e C1, aplicamos a transformação f1 nos vértices A, B e C.
Dessa forma teremos:
f1(x, y) = (x, –⇒ A1 == f1(– 3,= (– 3, – 1)
= (1, 3)
1)
y)
f1(A)
⇒ B1 = f1(B) = f1(1, –= (3, – 3)
⇒ C1 = f1(C) 3)
= f1(3, 3)
Para encontrarmos os vértices A2, B2 e C2, aplicamos a transformação f2 nos vértices A1, B1 e C1.
Assim:
f2(x, y) = (2x, 2y) ⇒ A2 = f2(A1) = f2(– 3, –= (– 6, – 2)
= (2, 6)
⇒ B2 = f2(B1) 1)
⇒ C2 = f2(C1) = f2(1, 3) = (6, – 6)
= f2(3, – 3)
• Outra forma de encontrarmos os vértices A1, B1 e C1 é utilizando a matriz que representa a
⎡ 1 0⎤
⎥ . Dessa forma temos:
⎣0 − 1⎦
⎡ 1 0⎤ ⎡− 3⎤
⎡− 3⎤
⎡ 1 0⎤ ⎡ xA ⎤
A1 = f1(xA, yA) ⇒ A1 = [ f1]A ⇒ A1 = ⎢
⇒ A1 = ⎢
⇒ A1 = ⎢ ⎥ ou, A1 = (–
⎢
⎥
⎥
⎢
⎥
⎥
⎣0 − 1⎦ ⎣ yA ⎦
⎣0 − 1⎦ ⎣ 1⎦
⎣ − 1⎦
transformação reflexão dada por [ f1 ] = ⎢
3, – 1)
⎡1
0⎤ ⎡ x ⎤
⎡1
0⎤ ⎡ 1⎤
⎡1⎤
B
B1 = f1(xB, yB) ⇒ B1 = [ f1]B ⇒ B1 = ⎢
⎥ ⎢ ⎥ ⇒ B1 = ⎢0 − 1⎥ ⎢− 3⎥ ⇒ B1 = ⎢3⎥ ou, B1 = (1,
⎣0 − 1⎦ ⎣ yB ⎦
⎣ ⎦
⎣
⎦⎣ ⎦
3)
⎡1
0⎤ ⎡ x ⎤
⎡1
0⎤ ⎡3⎤
⎡ 3⎤
C
C1 = f1(xC, yC) ⇒ C1 = [ f1]C ⇒ C1 = ⎢
⎥ ⎢ y ⎥ ⇒ C1 = ⎢0 − 1⎥ ⎢3⎥ ⇒ C1 = ⎢− 3⎥ ou, C1 = (3, –
−
0
1
⎣
⎦ ⎣ C⎦
⎣
⎦⎣ ⎦
⎣ ⎦
3).
⎡2 0⎤
⎥ , que representa a transformação f2:
⎣0 2⎦
⎡− 6⎤
⎡2 0⎤ ⎡− 3⎤
⎡ 2 0⎤ ⎡ xA1 ⎤
A2 = f2(xA1, yA1) ⇒ A2 = [ f2]A1 ⇒ A2 = ⎢
⎥ ⎢ y ⎥ ⇒ A2 = ⎢0 2⎥ ⎢ − 1⎥ ⇒ A2 = ⎢− 2⎥ ou, A2 =
0
2
⎣
⎦ ⎣ A1 ⎦
⎣ ⎦
⎣
⎦⎣ ⎦
Da mesma forma, procedemos com a matriz [ f 2 ] = ⎢
(– 6, – 2)
⎡ 2 0⎤ ⎡ x ⎤
⎡2 0⎤ ⎡ 1⎤
⎡ 2⎤
B1
B2 = f2(xB1, yB1) ⇒ B2 = [ f2]B1 ⇒ B2 = ⎢
⎥ ⎢ y ⎥ ⇒ B2 = ⎢0 2⎥ ⎢− 3⎥ ⇒ B2 = ⎢6⎥ ou, B2 = (2,
0
2
⎣ ⎦
⎣
⎦⎣ ⎦
⎣
⎦ ⎣ B1 ⎦
6)
⎡2 0⎤ ⎡ x ⎤
⎡2 0⎤ ⎡ 3⎤
⎡ 6⎤
C1
C2 = f2(xC1, yC1) ⇒ C2 = [ f2]C1 ⇒ C2 = ⎢
⎢ y ⎥ ⇒ C2 = ⎢
⎥ ⎢ ⎥ ⇒ C2 = ⎢− 6⎥ ou, C1 =
⎥
⎣0 2⎦ ⎣− 3⎦
⎣ ⎦
⎣ 0 2 ⎦ ⎣ C1 ⎦
(6, – 6)
• Observe que se trata de uma composição de funções e, portanto, podemos representar as duas
transformações por uma só lei matemática. Assim, designando por f a lei que transforma os vetores A, B e C em A2, B2 e C2 temos:
64
f (x, y) = f2(f1(x, y)) = f2(x, – y) = (2x, – 2y).
Assim, a transformação f1 seguida de f2 pode ser escrita dessa forma:
(x, y) 6 (2x, – 2y) ou f (x, y) = (2x, – 2y).
Matricialmente, procederíamos da seguinte forma
⎡2 0⎤ ⎡ 1 0⎤ ⎡ x ⎤
[ f ( x, y )] = ⎢
⎥⎢ ⎥
⎥⎢
⎣0 2⎦ ⎣0 − 1⎦ ⎣ y ⎦
ou seja, a matriz da transformação f, [ f ], é obtida pelo produto da matriz da transformação f2, [
f2], pela matriz da transformação f1, [ f1]. (Cuidado! O produto de matrizes não é comutativo.)
⎡ 2 0 ⎤ ⎡ 1 0⎤
[ f ] = [ f 2 ][ f1 ] ⇒ [ f ] = ⎢
⎥ ⇒[f]=
⎥⎢
⎣0 2⎦ ⎣0 − 1⎦
0⎤
⎡2
⎢0 − 2⎥
⎣
⎦
• Vamos utilizar a matriz [ f ] para encontrar os vértices A2, B2 e C2, resultado final das transformações:
⎡2
0⎤ ⎡− 3⎤
⎡ − 6⎤
⎡2
0⎤ ⎡ 1⎤
⎡ 2⎤
⎡2
0⎤ ⎡3⎤
A2 = [ f ]A = ⎢
⎥⎢ ⎥ = ⎢ ⎥
⎣0 − 2⎦ ⎣ 1⎦ ⎣− 2⎦
B2 = [ f ]B = ⎢
⎥⎢ ⎥ = ⎢ ⎥
⎣0 − 2⎦ ⎣− 3⎦ ⎣6⎦
⎡ 6⎤
C2 = [ f ]C = ⎢
⎥⎢ ⎥ = ⎢ ⎥.
⎣0 − 2⎦ ⎣3⎦ ⎣− 6⎦
65