ver comentário

ITA
ETAPA
QUESTÃO 20
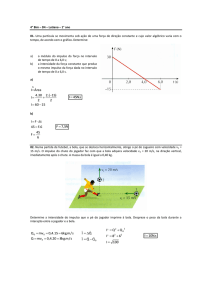
Água de um reservatório é usada para girar um moinho de raio R com velocidade angular ω
constante graças ao jato que flui do orifício de área S situado a uma profundidade h do seu nível. Com o jato incidindo perpendicularmente em cada pá, com choque totalmente inelástico,
calcule o torque das forças de atrito no eixo do moinho, sendo ρ e g, respectivamente, a massa,
específica da água e a aceleração da gravidade.
h
R
d)2ρghRS e1 –
c) 2ρghRS e1 –
b)ρR2Sω 2gh
a) 2ρghRS
ωR
o
2gh
e) ρR2Sω 2gh e1 –
2gh
o
ωR
ωR
o
2gh
ver comentário
De acordo com a conservação da energia, a velocidade com a qual a água sai do reservatório
é dada por v = 2gh .
Após o choque, inelástico, uma porção da água com massa ∆m terá velocidade ωR. Sendo
assim, a variação de momento linear dessa massa de água será dada por ∆p = ∆m ⋅ (v – ωR).
Para determinar a massa de água que atinge uma das pás num intervalo de tempo ∆t, vamos considerar uma porção cilíndrica que emerge do orifício com área da base S e comprimento L. A massa contida nesse cilindro é dada por ∆m = ρ ⋅ S ⋅ L.
Nota-se que após um intervalo de tempo ∆t a pá se desloca ωR∆t. Portanto, o comprimento
do cilindro que atinge a pá é dado por L = (v – ωR)∆t.
Portanto a massa do cilindro será:
∆m = ρS(v – ωR)∆t
Sendo assim, a força média aplicada pela água sobre uma pá do moinho é dada por:
F=
ωR 2
Tp
= ρS(v – ωR)2 & F = ρSv2 d1–
n
v
Tt
ITA
ETAPA
O torque das forças de atrito tem o mesmo módulo dos torques da porção de água que
atinge a pá, logo:
M = R ⋅ F = ρSv2R d1–
ωR 2
n & M = 2ρghRS f 1 –
v
Observação:
ωR 2
p
2gh
ωR
, que resulta do movimento relativo entre a água e
2gh
cada pá do moinho, o torque seria M = 2ρghRS, como indica a alternativa A.
Caso fosse desprezado o fator