1. (Ime 2013) Um corpo de 300 g de massa é lançado

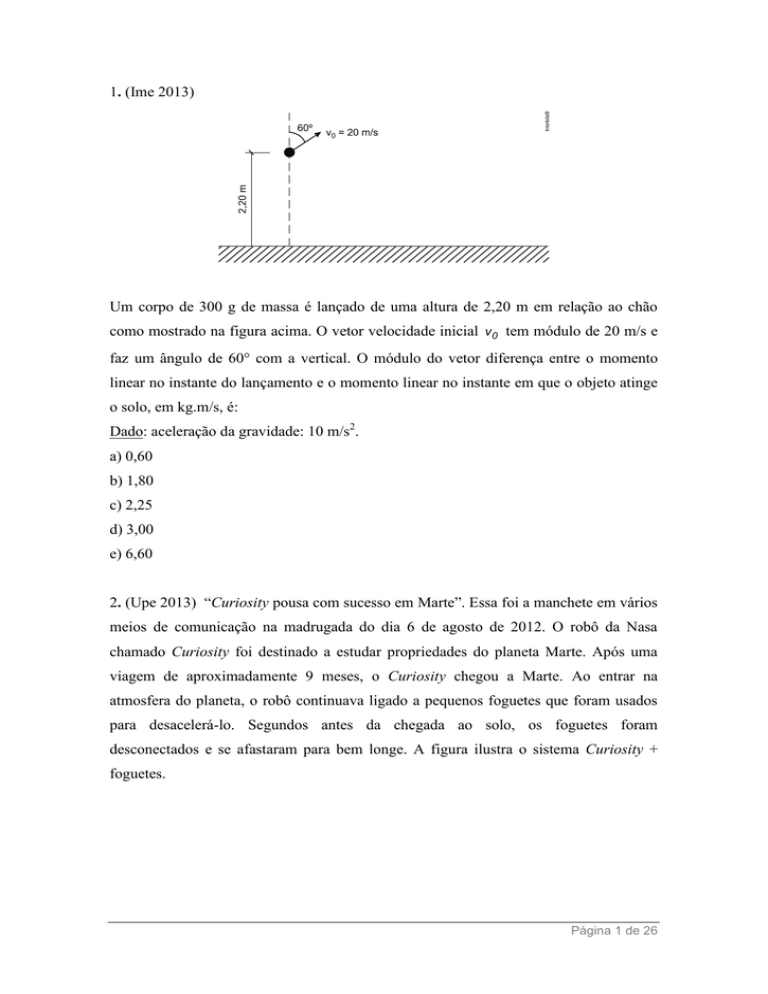
1. (Ime 2013)
Um corpo de 300 g de massa é lançado de uma altura de 2,20 m em relação ao chão
como mostrado na figura acima. O vetor velocidade inicial v0 tem módulo de 20 m/s e
faz um ângulo de 60° com a vertical. O módulo do vetor diferença entre o momento
linear no instante do lançamento e o momento linear no instante em que o objeto atinge
o solo, em kg.m/s, é:
Dado: aceleração da gravidade: 10 m/s2.
a) 0,60
b) 1,80
c) 2,25
d) 3,00
e) 6,60
2. (Upe 2013) “Curiosity pousa com sucesso em Marte”. Essa foi a manchete em vários
meios de comunicação na madrugada do dia 6 de agosto de 2012. O robô da Nasa
chamado Curiosity foi destinado a estudar propriedades do planeta Marte. Após uma
viagem de aproximadamente 9 meses, o Curiosity chegou a Marte. Ao entrar na
atmosfera do planeta, o robô continuava ligado a pequenos foguetes que foram usados
para desacelerá-lo. Segundos antes da chegada ao solo, os foguetes foram
desconectados e se afastaram para bem longe. A figura ilustra o sistema Curiosity +
foguetes.
Página 1 de 26
A massa dos foguetes varia continuamente, enquanto eles queimam combustível e
produzem a exaustão dos gases. A propulsão dos foguetes que fizeram desacelerar o
Curiosity é um exemplo notável da
a) Lei da Inércia.
b) Lei de Kepler.
c) Conservação da Energia.
d) Conservação da Quantidade de Movimento.
e) Lei da Gravitação Universal.
3. (Epcar (Afa) 2012) De acordo com a figura abaixo, a partícula A, ao ser abandonada
de uma altura H, desce a rampa sem atritos ou resistência do ar até sofrer uma colisão,
perfeitamente elástica, com a partícula B que possui o dobro da massa de A e que se
encontra inicialmente em repouso. Após essa colisão, B entra em movimento e A
retorna, subindo a rampa e atingindo uma altura igual a
a) H
b)
H
2
c)
H
3
Página 2 de 26
d)
H
9
4. (Uerj 2012)
Em uma partida de tênis, após um saque, a bola, de massa
aproximadamente igual a 0,06 kg, pode atingir o solo com uma velocidade de 60 m/s.
Admitindo que a bola esteja em repouso no momento em que a raquete colide contra
ela, determine, no SI, as variações de sua quantidade de movimento e de sua energia
cinética.
5. (Uftm 2012) Um pedreiro, ao mover sua colher, dá movimento na direção horizontal
a uma porção de massa de reboco, de 0,6 kg, que atinge perpendicularmente a parede,
com velocidade de 8 m/s. A interação com a parede é inelástica e tem duração de 0,1 s.
No choque, a massa de reboco se espalha uniformemente, cobrindo uma área de 20 cm2.
Nessas condições, a pressão média exercida pela massa sobre os tijolos da parede é, em
Pa,
a) 64 000.
b) 48 000.
c) 36 000.
d) 24 000.
e) 16 000.
6. (Ita 2012) 100 cápsulas com água, cada uma de massa m = 1,0 g, são disparadas à
velocidade de 10,0 m/s perpendicularmente a uma placa vertical com a qual colidem
inelasticamente. Sendo as cápsulas enfileiradas com espaçamento de 1,0 cm, determine
a força média exercida pelas mesmas sobre a placa.
7. (Fuvest 2012)
Página 3 de 26
Maria e Luísa, ambas de massa M, patinam no gelo. Luísa vai ao encontro de Maria
com velocidade de módulo V. Maria, parada na pista, segura uma bola de massa m e,
num certo instante, joga a bola para Luísa. A bola tem velocidade de módulo  , na

mesma direção de V . Depois que Luísa agarra a bola, as velocidades de Maria e Luísa,
em relação ao solo, são, respectivamente,
a) 0 ;   V
b)  ;   V / 2
c) m / M ; MV / m
d) m / M ; (m - MV) / (M  m)
e) (M V / 2 - m)/ M ; (m - MV / 2) / (M  m)
8. (Unifesp 2012) Um corpo esférico, pequeno e de massa 0,1 kg, sujeito a aceleração
gravitacional de 10 m/s2, é solto na borda de uma pista que tem a forma de uma
depressão hemisférica, de atrito desprezível e de raio 20 cm, conforme apresentado na
figura. Na parte mais baixa da pista, o corpo sofre uma colisão frontal com outro corpo,
idêntico e em repouso.
Considerando que a colisão relatada seja totalmente inelástica, determine:
a) O módulo da velocidade dos corpos, em m/s, imediatamente após a colisão.
b) A intensidade da força de reação, em newtons, que a pista exerce sobre os corpos
unidos no instante em que, após a colisão, atingem a altura máxima.
9. (Espcex (Aman) 2012) Um canhão, inicialmente em repouso, de massa 600 kg,
dispara um projétil de massa 3 kg com velocidade horizontal de 800 m s. Desprezando
todos os atritos, podemos afirmar que a velocidade de recuo do canhão é de:
a) 2 m s
Página 4 de 26
b) 4 m s
c) 6 m s
d) 8 m s
e) 12 m s
10. (Ufpe 2012) O martelo de ferro de 1,5 toneladas, de um bate-estaca, cai em queda
livre de uma altura de 5,0 m, a partir do repouso, sobre uma estaca de cimento. O
martelo não rebate após a colisão, isto é, permanece em contacto com a estaca. A força
exercida pela estaca sobre o martelo varia com o tempo de acordo com o gráfico a
seguir. Calcule o valor da força máxima Fmax , em unidades de 103 N . Despreze todas as
perdas de energia existentes entre o martelo e a guia, bem como com as demais
engrenagens.
11. (Ufsm 2011) Os mágicos são ilusionistas porque criam, no espectador, a ilusão de
que seus truques violam as leis físicas. Eles conseguem iludir porque desviam a atenção
do espectador. Numa festa de aniversário, um prato está sobre uma toalha que cobre
uma mesa. O prato e a toalha estão em repouso num referencial fixo na mesa. Então,
pronunciando abracadabras, o mágico puxa bruscamente a toalha horizontalmente,
retirando-a da mesa sem que o prato se desloque perceptivelmente. Esse truque pode ser
explicado, porque
a) não existe atrito entre o prato e a toalha.
b) nenhuma força atua sobre o prato.
c) a inércia do prato é muito maior do que a inércia da toalha.
Página 5 de 26
d) o módulo do impulso associado à força de atrito da toalha sobre o prato é muito
pequeno.
e) a força de resistência do ar cancela a força da toalha sobre o prato.
12. (G1 - cftmg 2011) Uma bola de tênis de massa m = 200g atinge uma raquete com
velocidade igual a 20,0 m/s e retorna, na mesma direção e em sentido contrario ao
inicial, com velocidade de 30,0 m/s. Se o tempo de interação entre bola e raquete e de
0,01 segundos, então, a forca média aplicada pelo tenista a raquete, em newtons, e igual
a
a) 1000.
b) 2000.
c) 3000.
d) 4000.
13. (Uesc 2011) Uma esfera de massa igual a 2,0kg, inicialmente em repouso sobre o
solo, é puxada verticalmente para cima por uma força constante de módulo igual a
30,0N, durante 2,0s.
Desprezando-se a resistência do ar e considerando-se o módulo da aceleração da
gravidade local igual a 10m / s2 , a intensidade da velocidade da esfera, no final de 2,0s,
é igual, em m/s, a
a) 10,0
b) 8,0
c) 6,0
d) 5,0
e) 4,0
14. (Ufjf 2011) A figura a seguir mostra um sistema composto por dois blocos de
massas idênticas mA = mB = 3,0 kg e uma mola de constante elástica k = 4,0 N / m. O
bloco A está preso a um fio de massa desprezível e suspenso de uma altura h = 0,8 m
em relação à superfície S, onde está posicionado o bloco B . Sabendo que a distância
entre o bloco B e a mola é d = 3,0 m e que a colisão entre os blocos A e B é elástica,
faça o que se pede nos itens seguintes.
Página 6 de 26
a) Usando a lei de conservação da quantidade de movimento (momento linear), calcule
a velocidade do bloco B imediatamente após a colisão do bloco A.
b) Calcule o deslocamento máximo sofrido pela mola se o atrito entre o bloco B e o solo
for desprezível.
c) Calcule a distância deslocada pelo bloco B em direção à mola, se o atrito cinético
entre o bloco B e o solo for igual a  c = 0,4. Nesse caso, a mola será comprimida pelo
bloco B? Justifique.
15. (Ifsp 2011) Existe um brinquedo de criança que é constituído de um pêndulo de três
bolinhas de mesma massa e comprimentos iguais. A brincadeira consiste em abandonar
uma bolinha X de uma altura H, acima das outras duas Y e W, que estão em repouso
(figura 1). Quando a bolinha X colidir com as duas, todas ficam grudadas e o conjunto
atinge uma altura h acima da posição inicial de Y e W (figura 2).
Se desconsiderarmos qualquer tipo de atrito, o valor de h em função de H será de:
a)
H
2
b)
H
3
Página 7 de 26
c)
H
6
d)
H
8
e)
H
9
16. (Ufsm 2011) O estresse pode fazer com que o cérebro funcione aquém de sua
capacidade. Atividades esportivas ou atividades lúdicas podem ajudar o cérebro a
normalizar suas funções.
Num certo esporte, corpos cilíndricos idênticos, com massa de 4kg, deslizam sem atrito
sobre uma superfície plana. Numa jogada, um corpo A movimenta-se sobre uma linha
reta, considerada o eixo x do referencial, com velocidade de módulo 2m/s e colide com
outro corpo, B, em repouso sobre a mesma reta. Por efeito da colisão, o corpo A
permanece em repouso, e o corpo B passa a se movimentar sobre a reta. A energia
cinética do corpo B, em J, é
a) 2.
b) 4.
c) 6.
d) 8.
e) 16.
17. (Uepg 2011) Um projétil de massa m é projetado horizontalmente com velocidade
v0 contra um pêndulo vertical de massa M, inicialmente em repouso. O projétil aloja-se
no pêndulo e, devido ao choque, o conjunto sobe até a altura h relativamente à posição
inicial do pêndulo (ver figura abaixo). Sobre esse evento físico, assinale o que for
correto.
01) O choque é perfeitamente inelástico.
02) A energia mecânica do sistema foi conservada.
Página 8 de 26
04) A velocidade v do sistema imediatamente após o choque é menor que a velocidade
v0 do projétil.
08) A velocidade v0 do projétil é dada por, v 0 
16) A altura h é igual a
mM
2gh.
m
v2
.
2g
18. (Fgvrj 2011) Leonardo, de 75 kg, e sua filha Beatriz, de 25 kg, estavam patinando
em uma pista horizontal de gelo, na mesma direção e em sentidos opostos, ambos com
velocidade de módulo v = 1,5 m/s. Por estarem distraídos, colidiram frontalmente, e
Beatriz passou a se mover com velocidade de módulo u = 3,0 m/s, na mesma direção,
mas em sentido contrário ao de seu movimento inicial. Após a colisão, a velocidade de
Leonardo é
a) nula.
b) 1,5 m/s no mesmo sentido de seu movimento inicial.
c) 1,5 m/s em sentido oposto ao de seu movimento inicial.
d) 3,0 m/s no mesmo sentido de seu movimento inicial.
e) 3,0 m/s em sentido oposto ao de seu movimento inicial.
19. (Unifesp 2011) Uma pequena pedra de 10g é lançada por um dispositivo com
velocidade horizontal de módulo igual a 600 m/s, incide sobre um pêndulo em repouso
e nele se engasta, caracterizando uma colisão totalmente inelástica. O pêndulo tem 6,0
kg de massa e está pendurado por uma corda de massa desprezível e inextensível, de 1,0
m de comprimento. Ele pode girar sem atrito no plano vertical, em torno da extremidade
fixa da corda, de modo que a energia mecânica seja conservada após a colisão.
Considerando g = 10,0 m/s2, calcule
a) a velocidade do pêndulo com a pedra engastada, imediatamente após a colisão.
Página 9 de 26
b) a altura máxima atingida pelo pêndulo com a pedra engastada e a tensão T na corda
neste instante.
20. (Fgv 2010) Um brinquedo muito simples de construir, e que vai ao encontro dos
ideais de redução, reutilização e reciclagem de lixo, é retratado na figura.
A brincadeira, em dupla, consiste em mandar o bólido de 100 g, feito de garrafas
plásticas, um para o outro. Quem recebe o bólido, mantém suas mãos juntas, tornando
os fios paralelos, enquanto que, aquele que o manda, abre com vigor os braços,
imprimindo uma força variável, conforme o gráfico.
Considere que:
- a resistência ao movimento causada pelo ar e o atrito entre as garrafas com os fios
sejam desprezíveis;
- o tempo que o bólido necessita para deslocar-se de um extremo ao outro do brinquedo
seja igual ou superior a 0,60 s.
Página 10 de 26
Dessa forma, iniciando a brincadeira com o bólido em um dos extremos do brinquedo,
com velocidade nula, a velocidade de chegada do bólido ao outro extremo, em m/s, é de
a) 16.
b) 20.
c) 24.
d) 28.
e) 32.
21. (Ita 2010) Uma massa m1 com velocidade inicial V0 colide com um sistema massamola m2 e constante elástica k, inicialmente em repouso sobre uma superfície sem
atrito, conforme ilustra a figura. Determine o máximo comprimento de compressão da
mola, considerando desprezível a sua massa.
22. (Ufrj 2010) Um menino de 40 kg de massa corre em movimento retilíneo horizontal
em cima de uma prancha de 8,0 kg de massa que desliza sobre um piso horizontal,
conforme indica a figura. Não há qualquer atrito entre a prancha e o piso, embora haja
atrito entre o menino e a prancha. O movimento do menino ocorre com aceleração
constante de módulo 0,20 m/s2 e sentido para a esquerda, em relação ao piso.
a) Indique o sentido da componente horizontal da força que a prancha exerce sobre o
menino e calcule seu módulo.
b) Indique o sentido da aceleração da prancha relativa ao piso e calcule seu módulo.
Página 11 de 26
Gabarito:
Resposta da questão 1:
[E]
Q  Qf  Qi  Q  Qi  Qf
| Q || Qi  Qf | Q
Pelo teorema do impulso, temos:
Q  F.t
F  P  m.g
Q  F.t  Q  m.g.t (eq.1)
Vamos determinar o t analisando o lançamento oblíquo, considerando como
referencial o chão, ou seja, S0  2,2m , S  0 e VY  V0 .cos60º .
S  VY .t 
a.t2
g.t2
10.t2
 S  S0  VY .t 
 0  2,2  V0 .cos60º.t 

2
2
2
 2,2  20.0,5.t  5.t2  t2  2.t  0,44  0
Resolvendo a equação de segundo grau, teremos raízes: t1  2,2s e t2  2,2s .
Considerando a raiz positiva e substituindo na eq.1, teremos:
Q  m.g.t  300x103.10.2,2  Q  6,60kg.m
s
Resposta da questão 2:
[D]
Página 12 de 26
Para pequenos intervalos de tempo, o sistema formado pelo robô e pelos gases pode ser
considerado isolado de forças externas e, portanto, há conservação da quantidade de
movimento.
Resposta da questão 3:
[D]
Iremos resolver a questão em três partes:
– Primeira: descida da partícula A pela rampa;
– Segunda: colisão entre as partículas A e B na parte mais baixa da rampa;
– Terceira: retorno da partícula A, subindo a rampa novamente e atingindo uma nova
altura h.
> Primeira parte: descida da partícula A.
Considerando como um sistema conservativo a descida da partícula A, teremos:
Em  Em'  Ep  Ec  mgH 
mV2
 V2  2gH  V  2gH , em que V é a velocidade da
2
partícula A na parte mais baixa da rampa.
> Segunda parte: colisão entre as partículas A e B:
Considerando a colisão como um sistema isolado, teremos:
Página 13 de 26






Qfinal  Qinicial  QA final  QBfinal  QAinicial  QBinicial  m.V ' 2m.V 'B  m.V  2m.VB
Dividindo a equação por m e substituindo os valores, teremos:
m.V ' 2m.V 'B  m.V  2m.VB  V ' 2.V 'B  V  2.VB  V ' 2.V 'B  2gH  2.0  V ' 2.V 'B  2gH
V ' 2.V 'B  2gH (eq.1)
Como a colisão foi perfeitamente elástica (e = 1), teremos:
e
V 'B  V '
V 'B  V '
1
 V 'B  V '  2gH  V 'B  2gH  V '
V  VB
2gH  0
V 'B  2gH  V ' (eq.2)
Substituindo a “eq.2” na “eq.1”, teremos:
V' 2.V'B  2gh  V' 2.( 2gH  V')  2gh  3.V'   2gH  V'  
2gH
3
Ou seja, concluímos que a partícula A, após a colisão, volta a subir a rampa com uma

velocidade V' de intensidade
2gH
:
3
Página 14 de 26
> Terceira parte: retorno da partícula A, subindo a rampa e atingindo uma nova altura h:
Considerando que a partícula A suba a rampa em um sistema conservativo e que no
ponto mais alto ela se encontra em repouso, teremos:
Emf  Ep  mgh
Emi  Ec 
mV '2
2
Emf  Emi  mgh 
mV '2
2
Dividindo a equação por m e substituindo os valores, teremos:
2
 2gH 
2gH


2
3 
mV '
H

mgh 
 gh 
 gh  9  h 
2
2
2
9
Resposta da questão 4:
Variação da quantidade de movimento:
ΔQ  m.ΔV  forma escalar
ΔQ  0,06.(60  0)  0,06.60  3,6
 ΔQ  3,6 kg  m s
Variação da energia cinética:
Página 15 de 26
ΔEC  EC.F  EC.0  m.
V2
V2
 m. 0
2
2
602
0
2
 ΔEC  108 J
ΔEC  0,06.
Resposta da questão 5:
[D]
Analisando o problema através do teorema fundamental do impulso, temos:


I  ΔQ
Cuja análise escalar resulta:
F.Δt  m. Δv
Em que F representa a força média executada sobre a parede. Assim sendo:
F
m. Δv
Δt
F
0,6.8
 48N
0,1
Sendo a área da atuação da força igual a 20 cm2, temos:
p
F
48
480000


A 20.104
20
 p  24000Pa
Resposta da questão 6:
Página 16 de 26
Dados: m = 1 g = 10–3 kg; v0 = 10 m/s; S = 1 cm = 10–2.
O intervalo de tempo (t) entre duas colisões consecutivas é:
Δt 
ΔS 102

 Δt  103 s.
v0
10
Como as colisões são inelásticas, a velocidade final é v = 0. Aplicando o Teorema do
Impulso para cada cápsula:
Fm Δt  m Δv  Fm 
m Δv 103 0  10


Δt
103
Fm  10 N.
Resposta da questão 7:
[D]
Antes de jogar a bola, Maria e a bola estão em repouso, portanto a quantidade de
movimento desse sistema é nula. Como o sistema é mecanicamente isolado (a resultante
das forças externas é nula), apliquemos a ele a conservação da quantidade de
movimento:
Qsist antes  Qsistema depois
VMaria 
 0  m v  M VMaria 
 M VMaria  m v 
m v
.
M
Antes de agarrar a bola que tem velocidade v, Luísa tem velocidade -V. Aplicando
novamente a conservação da quantidade de movimento:
Qsist antes  Qsist depois
VLuísa 
 m v  M V  m  M VLuísa 
m v M V
mM
Resposta da questão 8:
a) Pela conservação da energia mecânica, calculamos a velocidade (v), antes da colisão,
do corpo esférico que é abandonado.
Página 17 de 26
Dados: v0 = 0; H = R = 20 cm = 0,2 m; g = 10 m/s2.
mv2
inicial
final
EMec
 EMec
 mgR 
2
 v  2gR  2 10 0,2   v  2 m / s.
b) Como o choque é inelástico, pelo teorema do sistema isolado, calculamos a
velocidade (v’) do conjunto após a colisão.
depois
Qantes
 mv  2mv '  v ' 
sist  Qsist
v 2

2 2
 v '  1 m / s.
Usando novamente a conservação da energia mecânica, calculamos a altura (h) atingida
pelo conjunto formado pelos dois corpos esféricos.
inicial
final
EMec
 EMec

mv '2
v '2 12
 mgh  h 

2
2g 20
 h  0,05 m.
Nessa altura, a velocidade se anula. Então a intensidade da forma normal Fn  aplicada
pela pista tem a mesma intensidade da componente radial Pn  da força peso do
conjunto.
Na figura, as medidas estão expressas em cm.
No triângulo hachurado:
cos  
15
 0,75.
20
Fn  Pn  2mgcos   2  0,110  0,75   Fn  1,5 N.
Resposta da questão 9:
[B]
Página 18 de 26
Como o sistema é isolado, há conservação da quantidade de movimento. Portanto:
MV  mv  0  600V  3x800  V  4,0 m/s.
Resposta da questão 10:
O gráfico apresentado é de F x t, ou seja, a área sob a sua curva representa o impulso
(I=F.t), que por sua vez, representa a variação da quantidade de movimento
(I  Q  m.V). Sendo assim, concluímos que: m.  V = I = área sob a curva do
gráfico.
Para determinarmos a velocidade do martelo ao bater na estaca, vamos considerar um
sistema conservativo:
Ec  Ep 
m.V2
 m.g.h  V  2.g.h  V  2.10.5  V  10m / s
2
Como o martelo perde toda a sua velocidade após a colisão com a estaca: | V | 10m / s .
A
figura
área 
sob
a
curva
do
gráfico
é
um
trapézio
e
sua
área
será:
(B  b).alt (0,3  0,1).Fmax

 0,2.Fmax
2
2
m.  V = I = área sob a curva do gráfico
m = 1,5 ton = 1500 kg
m.V  área  1500.10  0,2.Fmax
Fmax  75x103 N.
Resposta da questão 11:
[D]
Quando a toalha é puxada, a força de atrito entre a toalha e o prato tende a trazer o prato
junto com a toalha. Porém, se o puxão é suficientemente forte e brusco, a variação da
quantidade de movimento do prato seria muito alta, não havendo impulso de intensidade
capaz de proporcioná-la. Podemos também pensar que a força de atrito exigida para que
Página 19 de 26
o prato acompanhe a toalha e maior que a força de atrito estática. Assim, o prato
escorrega em relação à toalha.
Resposta da questão 12:
[A]
FR  m.a  m.
ΔV
30  (20)
 0,2x
 1000N .
Δt
0,01
Resposta da questão 13:
[A]
Usando o teorema do impulso, vem:
 

IR  Q  Q0  F  Pt  m( V  V0 )  (30  20).2  2v  v  10m / s .
Resposta da questão 14:
a) Dados: mA = mB = m = 3 kg; h = 0,8 m; v0A = v0B = 0 e g = 10 m/s2.
Desprezando a resistência do ar, pela conservação da energia mecânica,
calculamos a velocidade (vA) do bloco A antes da colisão com o bloco B.
m g h
m v2A
2

vA  2 g h
 2 100,8
 v A  4 m/s.
 
Pela conservação da quantidade de movimento, calculamos a velocidade vB'
do bloco B depois da colisão. Convém salientar que, como a colisão entre A e B é
frontal e perfeitamente elástica, e as massas são iguais, ocorre troca de velocidades, ou
seja, após a colisão, o bloco A para e o bloco B segue com velocidade de 4 m/s. Mas
vamos aos cálculos e demonstremos isso.
depois
Qantes
sist  Qsist

m v A  m v 0B  m v'A  m vB'

4  v 'A  vB' (I).
Página 20 de 26
Como o choque é perfeitamente elástico, o coeficiente de restituição (e) vale 1.
e
vB'  v'A
v A  v0B
 1
vB'  v'A
4
'
'

vB  v A  4
  2 vB'  8
 '
'

vB  v A  4


vB'  v'A  4 (II).
vB'  4 m/s.
b) Se o atrito entre o bloco B e o solo for desprezível, esse bloco atingirá a mola com
velocidade 4 m/s, até que sua energia cinética transforme-se em energia potencial
elástica na mola, deformando-a de x. Assim, pela conservação da energia mecânica:
m v 'B2 k x2

2
2

x  vB'
m
3
4
k
4

x  2 3 m.
c) Dados: m = 3 kg; v0A = v  vB'  4 m/s;  = 0,4; d = 3 m e g = 10 m/s2.
Pelo teorema da energia cinética, o trabalho da força de atrito  WFat  é igual a
variação da energia cinética do bloco B. Seja D a distância percorrida por esse bloco até
parar. Então:
WFat  ECin
D

 Fat D  0 
v2
42

2  g 2  0,4 10 
m v2
2

  m g D 
m v2

2
 D = 2 m.
Como D < d, a mola não será comprimida pelo bloco B.
Resposta da questão 15:
[E]
O brinquedo é conhecido no meio Físico como Pêndulo de Newton.
Seja M a massa de cada bolinha.
– Calculando a velocidade da bolinha X antes do choque (Va), pela conservação da
energia mecânica:
Página 21 de 26
M Va2
 MgH
2
 Va = 2 g H . (I)
– Usando a conservação da quantidade de movimento, calculamos a velocidade (Vd) do
sistema formado pelas três bolinhas, depois do choque.
sistema
sistema
Qantes
 Qdepois

M Va  3M Vd

Vd 
Va
. (II)
3
Combinando (I) e (II):
Vd 
2 gH
. (III)
3
– Pela conservação da energia mecânica do sistema formado pelas três bolinhas, l
depois do choque, calculamos a altura final (h).
3 M Vd2
 3 Mgh
2

Vd2  2 g h. (IV)
2
 2 gH
Substituindo (III) em (IV):  3   2 g h



2 gH
 2 gh
9
h
H
9
Resposta da questão 16:
[D]
Pela conservação da Quantidade de Movimento:
m v A  m vB  m v 'A  m vB'
B
Cin
E
EBCin
m vB'2 4  2


2
2
 8 J.

2  0  0  v B'

v B'  2 m / s.
2

Resposta da questão 17:
01 + 04 + 08 + 16 = 29
01) Correta. A choque é perfeitamente inelástico, pois o projétil fica incrustado no
Página 22 de 26
bloco.
02) Incorreta. A energia mecânica somente se conserva em choques perfeitamente
elásticos.
04) Correta. Há perda de energia mecânica no choque inelástico.
08) Correta.
Pela conservação da energia mecânica após o choque:
mM 2
v  (m  M) g h  v  2 g h (I)
2
Pela conservação da quantidade de movimento no choque:
m v 0  (m  M)v  v 0 
mM
v (II)
m
Substituindo (I) e (II), vem:
v0 
mM
2gh.
m
16) Correta. Usando novamente a conservação da energia mecânica.
mM 2
v  M  m  g h
2

h
v2
.
2g
Resposta da questão 18:
[A]
Como o sistema é isolado de forças externas, podemos aplicar a conservação da
quantidade de movimento:


QTF  QTI  m1V1  m2 V2  m1u1  m2u2
75  1,5  25  1,5  75u1  25  3  u1  0
Resposta da questão 19:
Página 23 de 26
Dados: m = 10 g = 10–2 kg; v0 = 600 m/s; M = 6 kg = 6.000 g; h = 1 m; g = 10 m/s2.
a) A velocidade v1 do sistema pedra-pêndulo é calculada aplicando a conservação da
quantidade de movimento (Q) para antes e depois do choque:
depois
Qantes
sist  Qsist
v1 
6.000
6.010


m v 0  M  m v1

10  600  6.010 v1

v1  1 m/s.
b) Depois do choque o sistema é conservativo:
Einicial
mec
final
 Emec

M  m v12
2
 M  m  g h

v12
12
h

2 g 20

h = 0,05 m.
No ponto mais alto a velocidade é nula. Então, a resultante centrípeta é nula, ou
seja:
Py  T  0

m gcos θ  T
L h
 0,95 
 m g
 T  60,1

T 
 L 
 1 
T = 57,1 N.
Resposta da questão 20:
[C]
No gráfico da força pelo tempo apresentado no enunciado, o impulso é numericamente
igual a área do gráfico.
Página 24 de 26
I
0,6 (8)
 2,4 N.s
2
Pelo Teorema do Impulso: o impulso da força resultante é igual à variação da
quantidade de movimento (Q)
I = Q = m v  2,4 = 0,1 (v – 0)  v = 24 m/s.
Resposta da questão 21:
As variações de velocidades na colisão ocorrem somente pela interação entre a massa
m1 e a massa m2 formando, então, um sistema mecanicamente isolado. Portanto, há
conservação da quantidade de movimento do sistema que engloba m1, m2 e a mola.
A compressão máxima da mola ocorre quando os dois corpos têm a mesma velocidade
(V), ao final da fase de deformação. Assim:
fin
Qinsist  Qsist
 m1V0  m1  m2  V 
V
m1V0
. (equação 1)
m1  m2
O sistema é também conservativo, pois a força elástica responsável pelas variações de
velocidades é uma força conservativa. Então:
m1V02 kx2 m1  m2  V


. (equação 2)
2
2
2
2
fin
Einmec  Emec

Substituindo (1) em (2), vem:
2
 mV 
m V  k x  m1  m2   1 0  
 m1  m2 
2
1 0
2
m1V02  k x2 
m1V02 
m1  m2
m1  m2 
2
m12 V02 

m12 V02
m1 
2
 k x2  m1V02 1 
k x 
m1  m2
 m1  m2 
 m  m2  m1 
m2
2
k x2  m1V02  1

  x  m1V0
m1  m2
 m1  m2 
x  V0
m1m2
.
k m1  m2 
Página 25 de 26
Resposta da questão 22:
Dados: M = 40 kg; m = 8 kg; a = 2 m/s2.

a) No menino agem duas forças: a força peso ( P ) e a força de contato com a prancha



( F ). Essa força tem duas componentes: Fv , que é própria Normal, e Fh , que é força
responsável pela aceleração do menino.
Assim, do princípio fundamental da dinâmica (2ª lei de Newton):
Fh = M a  Fh = 40 (0,2)  Fh = 8,0 N.
b) Pelo princípio da ação reação, a componente horizontal da força que o menino exerce
na prancha também tem intensidade 8 N, porém em sentido oposto, que é também o
sentido da aceleração, como mostrado na figura a seguir.
Usando novamente o princípio fundamental, agora para a prancha, vem:
Fh = m ap  8 = 8 ap  ap = 1,0 m/s2.
Página 26 de 26