15 60I 2 )15.(2 2 30.4 I Área I - = - + = = s.N45I = 6 45 F 6.F 45 tFI

4° Bim – D4 – Lutiano – 1° ano
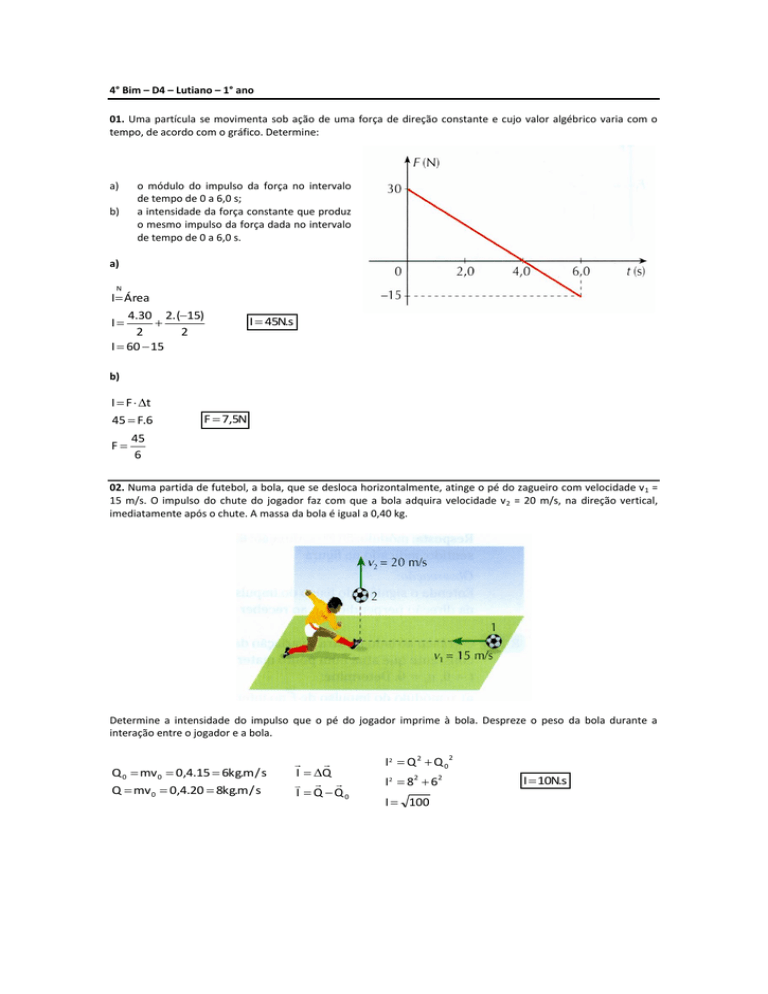
01. Uma partícula se movimenta sob ação de uma força de direção constante e cujo valor algébrico varia com o
tempo, de acordo com o gráfico. Determine:
a)
b)
o módulo do impulso da força no intervalo
de tempo de 0 a 6,0 s;
a intensidade da força constante que produz
o mesmo impulso da força dada no intervalo
de tempo de 0 a 6,0 s.
a)
N
I  Área
4.30 2.(15)

2
2
I  60  15
I
I  45N.s
b)
I  F  t
45  F.6
45
F
6
F  7,5N
02. Numa partida de futebol, a bola, que se desloca horizontalmente, atinge o pé do zagueiro com velocidade v 1 =
15 m/s. O impulso do chute do jogador faz com que a bola adquira velocidade v 2 = 20 m/s, na direção vertical,
imediatamente após o chute. A massa da bola é igual a 0,40 kg.
Determine a intensidade do impulso que o pé do jogador imprime à bola. Despreze o peso da bola durante a
interação entre o jogador e a bola.
Q 0  mv 0  0,4.15  6kg.m / s
Q  mv 0  0,4.20  8kg.m / s


I  Q
  
I  Q Q0
I2  Q 2  Q 0 2
I2  82  62
I  100
I  10N.s
03. Um casal participa de uma competição de patinação sobre o gelo. Em dado instante, o rapaz, de massa igual a
60 kg, e a garota, de massa igual a 40 kg, estão parados e abraçados frente a frente. Subitamente, o rapaz dá um
empurrão na garota, que sai patinando para trás com uma velocidade de módulo igual a 0,60 m/s.
v1
v2
m1
m2
+
Qual o módulo da velocidade do rapaz ao recuar, como consequência desse empurrão? Despreze o atrito com o
chão e o efeito do ar.


Q ANTES  Q DEPOIS
0  m1 v 1  m2 v 2
m1 v 1  m2 v 2
m1 v 1  m2 v 2
60v 1  40.0,6
v1  0,4m / s
04. Um jogador de hockey no gelo consegue imprimir uma velocidade de 162 km/h ao puck (disco), cuja massa é de
200 g. Considerando-se que o tempo de contato entre o puck e o stick (o taco) é da ordem de um centésimo de
segundo (Δt = 0,01 s), calcule a intensidade da força média impulsiva.
m  200g  0,2kg


I  Q
v0  0
F  t  mv  mv 0
v  162km/ h  45m / s
F  0,01  0,2.45  0
F  900N
05. A figura seguinte representa dois carrinhos A e B de massas m e 3m, respectivamente, que percorrem um
mesmo trilho retilíneo com velocidades escalares vA = 15 m/s e vB = 5,0 m/s:
vA
vB
Se o choque mecânico que ocorre entre eles tem coeficiente de restituição 0,2, determine os módulos das
velocidades escalares dos carrinhos após a interação.
Depois:
v'A


Q ANTES  Q DEPOIS
mA v A  mB v B  mA v'A mB v'B
15m  15m  m.v'A 3mv'B
v'B
30m  m.v'A 3mv'B
30  v'A 3v'B
v'A 3v'B  30
e
v REL . AFASTAMENT O
v REL . APROXIMAÇÃ O
v'B v'A
15  5
v'B v'A  2
v'B v'A  2
0,2 
 v'A 3v'B  30

 v'B v'A  2
4v'B  32
v'B  8m / s
(Para a direita)
v'B v'A  2
8  v'A  2
v'A  6m / s
(Para a direita)
Questão Extra – Desafio (Valor: 10,0)
Uma pequena bola de borracha maciça é solta do repouso de uma altura h0 = 1,0 m em relação a um piso liso e
sólido. A colisão da bola com o piso tem coeficiente de restituição e = 0,8. Calcule a altura máxima h atingida pela
2
bola, após a primeira colisão com o piso. Despreze os possíveis atritos e considere g = 10 m/s .
Relacionando a velocidade final da esfera (imediatamente antes de tocar o solo) e a altura inicial:
v 2  v 0 2  2gh
v 2  0  2g(0  h0 )
v 2  2gh0
v  2gh0
Após o choque:
e
e
e
v'  2gh
v REL . AFASTAMENT O
v REL . APROXIMAÇÃ O
v'
v
2gh
2gh0
e
2gh
2gh0
e
h
h0
e2 
h
h0
h  e 2  h0
h  (0,8)2 .1,0
h  0,64m