Física 2005

QUESTÃO 01
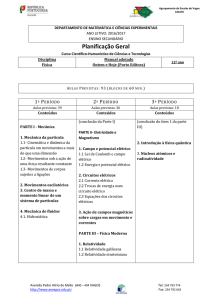
O gráfico abaixo mostra como variou a velocidade de um atleta durante uma disputa de 100 m rasos.
Sendo de 8,0 m/s a velocidade média deste atleta, pode-se afirmar que a velocidade v no instante em que ele cruzou a linha de
chegada era, em m/s,
a) 5,0
b) 3,5
c) 8,5
d) 10
Solução:
Do enunciado:
Vm = 8,0m/s
∆s = 100m
Portanto o tempo de prova foi: v m =
100
∆s
⇒ ∆t =
= 12,5s
8,0
∆t
A2
A3
A1
Do gráfico temos que ∆s ≅ A ; portanto:
∆s = ∆1+∆2+∆3
12.5,5
(12 + v).(12,5 − 8,5)
+ (8,5 − 5,5).12 +
2
2
v = 3,5m/s
100 =
ALTERNATIVA B
QUESTÃO 02
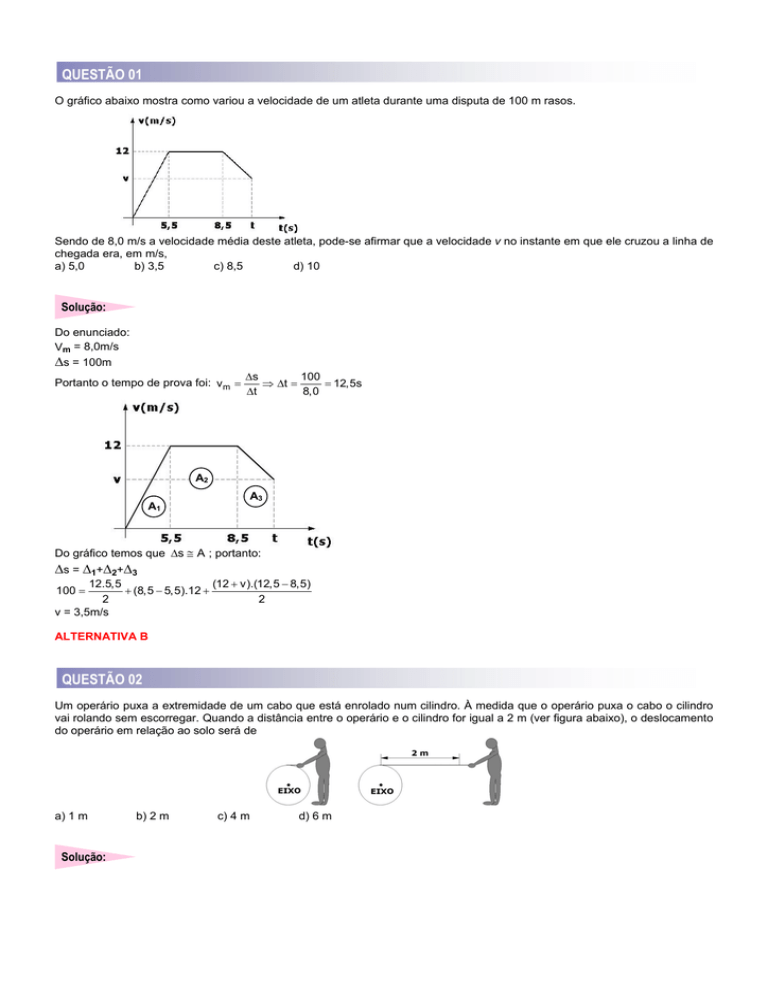
Um operário puxa a extremidade de um cabo que está enrolado num cilindro. À medida que o operário puxa o cabo o cilindro
vai rolando sem escorregar. Quando a distância entre o operário e o cilindro for igual a 2 m (ver figura abaixo), o deslocamento
do operário em relação ao solo será de
a) 1 m
Solução:
b) 2 m
c) 4 m
d) 6 m
2v
2v
v
x
2m
y
Considerando a velocidade do eixo do cilindro como v, a velocidade do operário será 2 v.
∆s
x
Para o eixo: vE = E ⇔ ∆tE =
∆tE
v
Para o operário: v o =
∆so
y
⇔ ∆t o =
2v
∆to
Como ∆tE = ∆t o :
x
y
=
⇔ y = 2x
v 2v
Sendo x + 2 = y , temos:
x + 2 = 2 x ⇔ x = 2m
Portanto o deslocamento y do operário em relação ao solo foi 4m.
ALTERNATIVA C
QUESTÃO 03
Analise as afirmativas abaixo sobre o movimento circular uniforme:
I – A velocidade vetorial tem direção variável.
II – A resultante das forças que atuam num corpo que descreve esse tipo de movimento não é nula.
III – O módulo da aceleração tangencial é nulo.
Está(ao) correta(s)
a) I apenas.
c) II e III apenas.
b) I e III apenas.
d) I, II e III.
Solução:
I – Correta:
uur
v1
Velocidade em 2 instantes.
uur
v2
II – Correta. No movimento circular sempre se tem uma resultante centrípeta.
III – Correta. Como o movimento é uniforme o módulo da velocidade é constante e a aceleração tangente é nula.
ALTERNATIVA D
QUESTÃO 04
O movimento da coroa dentada (A) de uma bicicleta é transmitido a uma catraca (B) localizada no eixo da roda traseira (C) por
meio de uma corrente. A opção que representa a bicicleta mais veloz para o mesmo número de pedaladas do ciclista é
a)
c)
b)
d)
Solução:
C
B
A
Tem-se:
v A = vB ⇒ w AR A = wBRB (I)
wB = w C
(II)
wC RA
=
w A RB
Quanto maior o movimento entre RA e RB, maior a freqüência da roda C, portanto o ciclista está mais rápido, sendo assim
desejável RA>RB.
Substituindo II em I: w A .R A = w C.RB ⇒
ALTERNATIVA A
QUESTÃO 05
Um avião a jato, cuja massa é de 40 toneladas, ejeta, durante 5 segundos, 100 kg de gás e esse gás sofre uma variação de
velocidade de 500 m/s.
Com base nessas informações, analise as seguintes afirmativas:
I – A variação da velocidade do avião é de 1,25 m/s.
II – A força aplicada no avião é de 104 N.
III – O impulso sofrido pelo avião vale 5.104 kg.m/s.
Está(ao) correta(s)
a) apenas I.
b) apenas I e II
c) apenas I e III.
d) I, II e III.
Solução:
III – Correta. O impulso sofrido pelo gás é dado por:
r
ur
I = ∆Q ⇒ I = Q f − Qi ⇒ I = mv f − mv i ⇒ I = m( ∆v)
I = 100.500 = 50000 kg.m / s
O impulso sofrido pelo gás tem a mesma intensidade do impulso sofrido pelo avião.
II – Correta.
r r
I = F.∆t ⇒ I = F.∆t ⇒ 50000 = F.5 ⇒ F = 104 N
I – Correta.
I = m.∆v (mostrado anteriormente)
⇒ 50000 = 40000.∆v = 1,25m / s
Obs.: Foi assumido que a variação da velocidade foi apenas em módulo, não em direção. Do contrário não há solução.
ALTERNATIVA B
QUESTÃO 06
Os satélites de comunicação são operados normalmente em órbitas cuja velocidade angular ω é igual à da Terra, de modo a
permanecerem imóveis em relação às antenas receptoras. Na figura abaixo, estão representados dois destes satélites, A e B,
em órbitas geoestacionárias e em diferentes alturas. Sendo a massa de A maior que a de B, pode-se afirmar que as relações
entre os módulos das velocidades vA e vB e os períodos de rotação TA e TB dos satélites A e B estão representados
corretamente na alternativa
a) vA = vB e TA = TB
b) vA < vB e TA < TB
c) vA > vB e TA = TB
d) vA > vB e TA > TB
Solução:
2π ⎞
⎛
Como w A = w B = w TERRA ⇒ TA = TB ⎜ w =
⎟
T ⎠
⎝
Tem-se:
v
v
w A = wB ⇒ A = B
R A RB
Como RA > RB, vA > vB
ALTERNATIVA C
QUESTÃO 07
Duas partículas são lançadas nos pontos A e B com a mesma velocidade v0, conforme indica a figura abaixo:
Enquanto a partícula de massa m passa por um trecho em elevação, a outra, de massa M, passa por uma depressão com a
mesma forma e “profundidade” h.
t
Desprezando-se quaisquer forças dissipativas, pode-se afirmar que a razão A entre os tempos gastos pelas partículas para
tB
atingirem os pontos D e C é
a) menor que 1, se m > M.
b) maior que 1, independentemente da razão m/M.
c) igual a 1, independentemente da razão m/M.
d) pode ser igual a 1, se m < M.
Solução:
Movimento A:
vx
vo
h
vo
A
Como o sistema é conservativo:
EmA = Emx
Ec A = Ep x + Ec x
mv o2
mv x 2
= m gh +
2
2
v x = v o2 − 2 gh
v x < vo
Movimento B:
vo
vo
B
h
vy
Como o sistema é conservativo:
EmB = Emy
EcB + EpB = Ec y ⇔
Mv y
Mv o2
+ Mgh =
2
2
2
v y = v o2 + 2 gh
v y > vo
No movimento A, a velocidade média v Am está no intervalo:
v o2 − 2 gh < v Am < v o
No movimento B, a velocidade média v Bm está no intervalo:
v o < vBm <
v o2 + 2 gh , como v mB > v mA , para um mesmo ∆s , tB < t A , portanto:
tA
> 1 independente da massa
tB
ALTERNATIVA B
QUESTÃO 08
Uma partícula de massa m é lançada obliquamente com velocidade v0 próxima à superfície terrestre, conforme indica a figura
abaixo. A quantidade de movimento adquirida pela partícula no ponto Q, de altura máxima, é
a) mv0
b) m
c) m 2gh
v 02 − 2gh
d) m
v 02
− gh
2
Solução:
Na direção y o movimento do corpo é uniformemente variado e sua aceleração é a aceleração da gravidade. Assim temos que:
2
v 2y = v0y
+ 2.a.∆y
No ponto de altura máxima vy = 0,
2
2
O2 = v0y
+ 2( −g).h ⇒ v 0y
= 2g.h
Sendo:
2
v 02 = v 0y
+ v 2x ⇒ v 2x = v 02 − 2gh ⇒ v x v 02 − 2gh
O módulo da quantidade de movimento do corpo na altura máxima é:
Q = m.v (v = vX)
Q = m v 02 − 2gh
ALTERNATIVA B
QUESTÃO 09
Os blocos A e B, de massas iguais a 2 kg e 3 kg, respectivamente, ligados por um fio ideal, formam um sistema que submetido
r
a ação de uma força constante F de intensidade 15 N, desloca-se com aceleração de 1 m/s2, conforme a figura abaixo. Se a
tração no fio que liga os blocos durante o deslocamento é de 9 N, pode-se afirmar que a razão entre os coeficientes de atrito
dos blocos A e B com a superfície vale
1
3
3
b)
2
a)
c)
2
3
d) 1
Solução:
Corpo A: F − FatA − T = mA ⋅ a ⇒ F − µ ANA − T = mA .a ⇒ µ ANA = F − T − mA ⋅ a
F − T − mA ⋅ a 15 − 9 − 2 ⋅ 1
=
= 0,2
mA ⋅ g
2 ⋅ 10
Corpo B:
⇒ µA =
T − FAT,B = mB ⋅ a ⇒ µBNB = T − mB ⋅ a ⇒ µB =
0,2
µ
9 − 3 ⋅1
= 0,2 . Logo A =
=1
⇒ µB =
µB 0,2
3 ⋅ 10
ALTERNATIVA D
T − mg ⋅ a
mB ⋅ g
QUESTÃO 10
Uma barra rígida homogênea de comprimento 2L e massa m está apoiada em dois suportes A e B, como mostra a figura
abaixo.
O gráfico que melhor indica a intensidade NA da reação que o apoio A exerce sobre a barra, em função da intensidade da força
F aplicada na extremidade é
a)
c)
b)
d)
Solução:
Equilíbrio de momentos em A:
L
L
m⋅g 1
P ⋅ − NA ⋅ L − F ⋅ = 0
NA =
− ⋅F
2
2
2
2
Logo, o gráfico de NA em função de F é dado por:
ALTERNATIVA A
QUESTÃO 11
Uma pessoa deita-se sobre uma prancha de madeira que flutua mantendo sua face superior no mesmo nível da superfície da
água.
A prancha tem 2 m de comprimento, 50 cm de largura e 15
cm de espessura. As densidades da água e da madeira são,
respectivamente, 1000 kg/m3 e 600 kg/m3. Considerando g=10 m/s2, pode-se afirmar que o peso da pessoa é
a) 600 N
c) 400 N
b) 700 N
d) 500 N
Solução:
FR = 0 (equilíbrio)
E = Ppessoa + Pprancha
⇒
M liq . Vdesl .g = Ppessoa + Mprancha . V .g ⇒
103 . ( 2.0,5.0,15 ) .10 = Ppessoa + 0,6.103.10 ⇒
Ppessoa = 600N
ALTERNATIVA A
QUESTÃO 12
Um líquido é colocado em um recipiente ocupando 75% de seu volume. Ao aquecer o conjunto (líquido + recipiente)
verifica-se que o volume da parte vazia não se altera. A razão entre os coeficientes de dilatação volumétrica do material do
γ
recipiente e do líquido M é
γL
a) 1
b)
3
4
4
3
1
d)
4
c)
Solução:
∆Vliq = ∆Vrec ⇒
V0 liq . γ liq . ∆θ = V0 rec . ∆θ ⇒
3
V0 . γ liq = V0 . γ rec ⇒
4
γ rec 3
=
γ liq 4
ALTERNATIVA B
QUESTÃO 13
Dispõe-se de uma balança de braços iguais e recipientes
idênticos contendo água cuja temperatura está indicada na figura de cada alternativa.
Aquela que mostra corretamente a situação de equilíbrio é
a)
c)
b)
d)
Solução:
Para a balança ficar em equilíbrio:
MPRATO A = MPRATO B ⇒ µ A .v A = µB .v B
Então quem é mais denso está contido em um menor volume.
ALTERNATIVA B
QUESTÃO 14
Para intervalos de temperaturas entre 5 °C e 50 °C, o calor específico (c ) de uma determinada substância varia com a
1
2
t+
temperatura ( t ) de acordo com a equação c =
, onde c é dado em cal/g°C e t em °C. A quantidade de calor
60
15
necessária para aquecer 60 g desta substância de 10 °C até 22°C é
a) 350 cal
c) 480 cal
b) 120 cal
d) 288 cal
Solução:
Cmed =
C10 + C22 0,3 + 0,5
cal
=
= 0, 4
2
2
gº C
Q = m.c.∆θ ⇒ Q = 60.0,4.12 ⇒ Q = 288cal
ALTERNATIVA D
QUESTÃO 15
A figura mostra uma barra metálica de secção reta constante sendo aquecida por uma chama de um fogareiro.
Quando se estabelece o regime estacionário de condução do calor, os termômetros A e C registram 200 °C e 80 °C,
respectivamente. Assim, a leitura no termômetro B será de
a) 100 °C
c) 140 °C
b) 125 °C
d) 155 °C
Solução:
θ(º C)
200
125
80
50
80
x(cm)
ALTERNATIVA B
QUESTÃO 16
Uma das aplicações do fenômeno da condução térmica é o uso de telas metálicas. Sabe-se que, colocando um recipiente de
vidro comum diretamente numa chama, ele se rompe. No entanto, interpondo uma tela metálica entre a chama e o recipiente, a
ruptura não acontece porque
a) os gases não queimam na região logo acima da tela, pois ali a temperatura não alcança valores suficientemente elevados.
b) há uma diferença entre os coeficientes de dilatação linear da tela e do recipiente.
c) a tela, por ser boa condutora, transmite rapidamente o calor para todos os pontos de sua própria extensão.
d) como são dois corpos, o aumento da temperatura não é suficiente para que seja verificada uma dilatação aparente.
Solução:
A condutibilidade térmica do metal é grande, desta maneira distribui rapidamente o calor.
ALTERNATIVA C
QUESTÃO 17
Um sistema é formado por dois reservatórios, A e B, de mesmo volume, ligados por um tubo longo, com área de secção
transversal constante e igual a S, conforme indica o esquema abaixo:
Enche-se os reservatórios com dois tipos de gases ideais, à mesma temperatura absoluta T0 e mesmo volume V0, que ficam
separados por um êmbolo que pode deslizar sem atrito. O êmbolo permanece no interior do tubo durante uma transformação
em que a temperatura do gás do reservatório A é duplicada, enquanto o gás do reservatório B é mantido sob temperatura
constante T0. Assim, o deslocamento do êmbolo foi de
2V0
c) 3SV0
a)
S
V
4V0
b) 0
d)
3S
3S
Solução:
Gás A:
p0 v 0 p A v A
p v
p v
p v
=
⇒ 0 0 = A A ⇒ p0 v 0 = A A
T0
TA
T0
2T0
2
Gás B:
p0 v 0 pB vB
p v
p v
=
⇒ 0 0 = B B ⇒ p0 v 0 = pB vB
T0
TB
T0
T0
Então:
vA
= UB
2
2U0 = UA + UB ⇒ v 0 = 3Sx ⇒ x =
v0
3S
ALTERNATIVA B
QUESTÃO 18
Com recursos naturais cada vez mais escassos, urge-se
pensar em novas fontes alternativas de energia. Uma das idéias sugeridas consiste em se aproveitar a energia térmica dos
oceanos, cuja água pode apresentar em uma superfície uma temperatura de 20 °C e no fundo temperatura em torno de 5,0 °C.
Um motor térmico operando neste intervalo de temperatura poderia ter um rendimento de
a) 3,0%
c) 9,0%
b) 7,5%
d) 27%
Solução:
Supondo que a máquina realize um ciclo de Carnot
T
5 + 273
η = 1− 2 ⇒ η = 1−
⇒ η = 3%
T1
20 + 273
ALTERNATIVA A
QUESTÃO 19
A figura mostra um cilindro que contém um gás ideal, com um êmbolo livre para se mover sem atrito. À temperatura de 27 °C, a
altura h na qual o êmbolo se encontra em equilíbrio vale 20 cm.
Aquecendo-se o cilindro à temperatura de 39 °C e mantendo-se inalteradas as demais características da mistura, a nova altura
h será, em cm,
a) 10,8
c) 20,8
b) 20,4
d) 10,4
Solução:
p1v1 p2v 2
=
transformação isobárica
T1
T2
AB .h1 AB .h2
v1 v 2
h2
20cm
=
⇒
⇒
=
=
T1 T2
T2
27 + 273 39 + 273
T1
⇒ h2 = 20,8cm
ALTERNATIVA C
QUESTÃO 20
Considere uma superfície de separação plana e horizontal entre o ar e a água. Se uma onda luminosa (L) e uma onda sonora
(S) incidem sobre essa superfície, com um ângulo de incidência θ, a opção que MELHOR ilustra a configuração física das
ondas luminosa e sonora, que se refratam é
a)
c)
b)
d)
Solução:
Para luz: como a luz percorre uma distância na água com uma velocidade menor que no ar ele se aproxima da normal.
Para o som: Como o som percorre uma distância com velocidade maior que no ar, ele se afasta da normal.
ALTERNATIVA B
QUESTÃO 21
Considere um objeto AB colocado sobre o eixo óptico de uma lente delgada biconvexa de raio de curvatura R, composta por
dois meios transparentes com índices de refração n1 = 2 e n2 = 4, como mostra a figura abaixo:
A imagem que se obterá com essa lente será
a)
c)
d)
b)
Solução:
A
B'
N1
B
A'
A
B''
N2
A''
B
ALTERNATIVA D
QUESTÃO 22
Considere o sistema apresentado na figura abaixo formado por um conjunto de três molas ideais e de constantes elásticas
iguais acopladas em paralelo e ligadas por meio de uma haste de massa desprezível a um segundo conjunto, formado por
duas massas M e m, tal que M = 2m. Considere, ainda, que o sistema oscila verticalmente em MHS (movimento harmônico
simples) com freqüência f1.
Se o fio ideal que une a massa m ao sistema for cortado simultaneamente com a mola central da associação de molas, o
sistema passará a oscilar com uma nova freqüência
f2, tal que a razão f2/f1 seja
a)1
c) 2
1
b)
2
d)
Solução:
f1 =
1
2π
3K
1 K
=
3m 2π m
f2 =
1
2π
2K
1 K
=
2m 2π m
f1
=1
f2
ALTERNATIVA A
2
3
QUESTÃO 23
Duas pequenas esferas eletrizadas com cargas positivas
iguais estão fixas nos pontos A e B, como mostra a figura abaixo:
Considerando apenas a influência de forças elétricas sobre uma carga q de prova em equilíbrio no ponto P, afirma-se que
I - se q é positiva, então está em equilíbrio estável em relação ao segmento AB.
II - se q é negativa, então está em equilíbrio instável em relação à mediatriz do segmento AB.
III - se q é negativa, então está em equilíbrio instável em relação ao segmento AB.
IV - se q é positiva, então está em equilíbrio estável em relação à mediatriz do segmento AB.
Estão corretas apenas
a) I e II .
c) III e IV.
b) II e III.
d) I e III.
Solução:
Instavel
+q
A
+Q
FR
FR
FR
+q
+q
B
+q
estavel
+Q
+q
FR
-q
FR
FR
+Q
FR
-q
-q
-q
+Q
FR
estavel
I Verdade, II Falso, III Verdade e IV Falso
ALTERNATIVA D
Instavel
QUESTÃO 24
Uma partícula de carga q e massa m penetra perpendicularmente às linhas de força de um campo elétrico
ur
uniforme E com a menor velocidade suficiente para sair sem tocar as placas, como mostra a figura abaixo:
A velocidade que ela deixa o campo elétrico é
1
1
⎡ Eq ⎛ L2 + 4d2 ⎞ ⎤ 2
⎜
⎟⎥
c) ⎢
⎢⎣ m ⎜⎝ 2d ⎟⎠ ⎥⎦
⎛ EqL2 ⎞ 2
⎟
a) ⎜
⎜ 2 md ⎟
⎝
⎠
1
1
⎡ Eq ⎛ L + d ⎞ ⎤ 2
d) ⎢
⎜ 2 ⎟⎥
⎣ m ⎝ L ⎠⎦
⎛ Eqd ⎞ 2
b) ⎜ 2
⎟
⎝ m ⎠
Solução:
y
v
d
2
x
L
A menor velocidade suficiente para sair sem tocar as placas ocorre quando a partícula sai tangenciando a placa inferior.
r
r
⎧⎪| R x |= m | a x |
r
r
R = ma → ⎨ r
r
⎪⎩| R y |= m | a y |
Desprezando o peso e considerando a força elétrica para baixo, tem-se:
r
| R x |= 0 → | a x |= 0 → mov. uniforme na direção x (MU)
r
r
|q|E
| R y |=| q | E →| a y |=
→ mov. uniformemente variado na direção y (MUV).
m
Para o MU: L = vt (1)
v y = v oy
ay t 2
d |q|E 2
−
t
2
2
2m
| q|E
+ ay t → v y = −
t (3)
m
Para o MUV: y = y o + v oy t +
→0=
( 2)
Eliminando t em (1) e (3), usando (2), tem-se:
v =L
|q|E
dm
( 4)
vy = −
A velocidade no instante t é v =
Substituindo-se (4) e (5), tem-se:
v = L2
| q | E | q | Ed
+
dm
m
| q | E dm
m
|q|E
v x2 + v y2
(5)
→v=
| q | E ⎛ L2 + d2 ⎞
⎜
⎟
m ⎝ d ⎠
Obs: Essa questão não tem alternativa correta.
QUESTÃO 25
Uma casca metálica esférica e não eletrizada envolve uma partícula eletrizada. Afirrma -se que
I - a casca esférica não interfere no campo elétrico gerado
pela partícula.
II - em pontos exteriores à casca o campo elétrico é nulo.
III - qualquer ponto interior à casca apresenta o mesmo potencial elétrico.
Está(ão) correta(s) apenas
a) I.
c) III.
b) II e III.
d) I e II.
Solução:
I) Correto. A carga interna produz uma distribuição de carga na casca, que gera seu próprio campo elétrico que se superpõe ao
campo elétrico da partícula. O campo elétrico resultante é alterado pela presença da casca, mas o campo individual da
partícula não se altera (ele se superpõe ao campo das cargas da casca.
II) Incorreto. O campo interno não se anula.
III)Incorreto se o enunciado referir-se à região da cavidade interna. O potencial é constante nos pontos da casca.
ALTERNATIVAA
QUESTÃO 26
Uma bateria fornece tensão constante U e está ligada a um fio homogêneo AB de seção transversal constante e comprimento
L, conforme mostra o circuito esquematizado abaixo:
Variando a posição do cursor C, a potência dissipada pelo fio AB será
L
L
a) máxima em x =
c) mínima em x =
4
2
L
L
b) máxima em x =
d) mínima em x =
2
4
Solução:
O circuito equivalente ao da figura é :
Pela 2º Lei de Ohm:
C
RCA
χ
A
p (L − χ )
RCA = p
RCB
δ
U
RCB =
A
A resistência equivalente da associação, então é:
Re q =
pχ ( L − χ )
RCA .RCB
=
RCA + RCB
AL
Assim a potência total dissipada nas resistências é
PT =
U2
Re q
⎛ R + RCB ⎞ 2
PT = ⎜ CA
⎟U
⎝ RCA .RCB ⎠
U2
A LU2
1
→ PT =
→ PT =
pχ ( L − χ )
p
−χ 2 + Lχ
AL
(
)
Essa potência é mínima quando o denominado −χ 2 + Lχ for máximo, isto é, no vértice da parábola f(x) = −χ + Lχ
Assim: χ v =
2
L
2
ALTERNATIVA C
QUESTÃO 27
No circuito abaixo, para que a bateria de f.e.m.
poderá ser igual a
a) 15
b) 20
ε1 e
resistência interna r1 funcione como receptor, o valor da resistência R
c) 25
d) 30
Solução:
ι1
ι2
1Ω
27v
1Ω
ιT
28v
ιT
R
Lei dos NOS:
ιT = ι1 + ι2
(1)
Lei das Malhas:
27 − ι1 + ι2 − 28 = 0
( 2)
28 − ι2 − RιT = 0 ( 3 )
Resolvendo o sistema, tem-se:
ι1 =
27 − R
1 + 2R
O componente 1 é receptor quando ι1 < 0 , isto é R > 27 .
ALTERNATIVA D
QUESTÃO 28
Considere o circuito da figura abaixo:
A leitura do voltímetro ideal V é
E
2E
c)
a)
2
3
E
3E
b)
d)
3
4
Solução:
Como o voltímetro é ideal, tem-se que o circuito é equivalente à
B
R
A
2R
2R
i'
i''
i
R
2R
i
C
R
2
i=
E
E
E
2R
E
E
E
∴ UAB =
e UAB =
4R
4
2
∴ UBC = UAC − UAB
E
UBC =
4
i' = i'' =
Obs.: Não há alternativa para a questão.
QUESTÃO 29
A figura abaixo mostra uma espira condutora quadrada, de lado l = 0,1 m, que gira com velocidade angular w constante em
torno do eixo z num campo magnético uniforme de intensidade B = 1T, na direção do eixo x.
A velocidade angular da espira para que seja induzida uma f.e.m. de, no máximo, 10 V é
a) 100 rad/s
b) 200 rad/s
c) 1000 rad/s
d) 2000 rad/s
Solução:
O fluxo do campo magnético é:
∅B = B. l2 cos θ(t)
∅B = B. l2 cos(wt + θ0 )
Pela lei de Faraday:
dθB
Eind =
dt
Eind = B l2 w | sen(wt + θ0 ) |
Eind max = B l2 w
10 = 1 . 0,12 w ⇒ w = 1000 rad/s
ALTERNATIVA C
QUESTÃO 30
O esquema a seguir é de um aparelho utilizado para medir a massa dos íons.
O íon de carga +q é produzido, praticamente em repouso, por meio da descarga de um gás, realizada na fonte F. O íon
ur
é, então, acelerado por uma d.d.p. U, penetrando, depois, num campo magnético B . No interior do campo, o íon descreve uma
órbita semicircular de raio r, terminando por atingir uma placa fotográfica, na qual deixa uma imagem. A massa do íon pode ser
calculada por
a)
b)
B2r 2 q
2U
2B2r 2
Uq
c)
d)
B2r 2
2U q
2B2r 2 q
U
Solução:
Como o sistema é conservativo no trecho de movimento acelerado:
Eim = Epf ⇒ Eic + Epi = Ecf + Epf ⇒ 0 + qvi =
⇒ q(vi − v f ) =
1 2
2qU
mv ⇒ v =
2
m
1 2
mv + qv f
2
(I)
Durante o movimento circular uniforme no campo magnético tem-se:
mv
r=
(2)
qB
Substituindo-se (1) em (2), tem-se:
2qU
m.
2 2 2
m ⇒m= r q B
r=
qB
2qU
m=
r 2qB2
2U
ALTERNATIVA A
Vestibular AFA 2005 – Física
Comentário
A prova seguiu o estilo tradicional dos anos anteriores. Algumas questões apresentaram problemas na elaboração do
enunciado ou nas alternativas. A questão 7 não se enquadra no conteúdo programático da prova nem consta na referência
Bibliográfica. Nas questões 24 e 28 não foi encontrado as alternativas corretas. Mesmo apresentados estes problemas foi uma
prova abrangente e bem elaborada.