Capítulo 06 - ComSizo.com.br

CAPÍTULO 6
Exercícios 6.1
2. Da hipótese e tendo em vista o critério de Cauchy para seqüência numérica, segue que
para cada x em B a seqüência numérica fn(x), n 1, é convergente. Assim, para cada x
em B existe um número f(x) para o qual tal seqüência converge. A função f : B 씮 ⺢
assim definida é tal que, para todo x em B,
lim fn ( x ) f ( x ).
n Æ
Exercícios 6.2
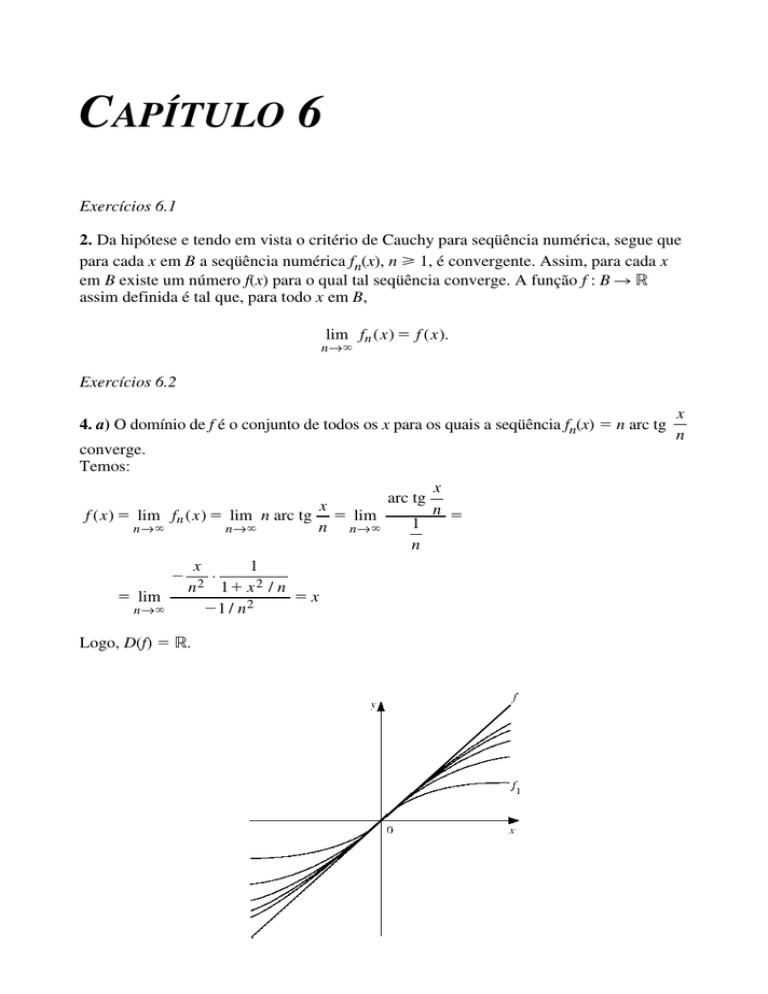
4. a) O domínio de f é o conjunto de todos os x para os quais a seqüência fn(x) n arc tg
converge.
Temos:
x
f ( x ) lim fn ( x ) lim n arc tg lim
n nÆ nÆ nÆ x
1
2 ◊
n 1 x 2 / n
lim
x
1 / n 2
nÆ Logo, D(f) ⺢.
arc tg
1
n
x
n x
n
b) Seja h(x) x n arc tg
Temos h( x ) x2
x
n
0.
x 2 n2
Então, h é crescente em [0, [. Segue que, para todo x [0, r],
x
r
0 x n arc tg r n arc tg .
n
n
Como lim (r n arc tg
n Æ
n n0 Þ r n arc tg
r
) 0, dado 0, existe n0 tal que
n
r
.
n
Segue que, para todo x [r, r],
n n0 Þ x n arc tg
x
.
n
Portanto, a seqüência fn ( x ) n arc tg
x
converge uniformemente a f(x) x em [r, r].
n
x
n
resulta que, dado , não existe n0 (que só depende desse ) que torne verdadeira a
c) Como, para todo n n0, lim x n arc tg
x Æ
afirmação para todo x ⺢, n n0 Þ fn ( x ) f ( x ) .
Portanto, a convergência não é uniforme em ⺢.
6. a) f ( x ) lim fn ( x ) lim
nÆ nÆ nx
0
1 n2 x 4
71
b) O valor máximo de fn ( x ) em [0, 1] é
x 4
3
1
pertence a [0, 1] e
2
4
3n
4
3
4
4
1
n2
e ocorre para x 4 2 , n 1;
3n
3
n2
tende a quando n tende a . Assim,
3
marcando uma faixa em torno do gráfico de f, 0 x 1, de amplitude 2, 0, sempre
existe uma fn cujo gráfico sai da faixa.
Então, fn não converge uniformemente a f em [0, 1].
c) Temos
1Ê
ˆ
1
fn ( x ) dx Ú f ( x ) dx 0
Ú0 Ë nlim
¯
0
Æ
lim
Ú
1
nÆ 0
1 1 2 nx
nx
lim
dx
dx 1 n2 x 4
nÆ 2 0 1 n2 x 4
1
1
1
lim
arc tg nx 2 lim [arc tg n arc tg 0] 0
2 nÆ nÆ 2
1 ◊ . 2 2
4
Ú
[
De e , segue
1Ê
]
ˆ
1
fn ( x ) dx lim Ú fn ( x ) dx
Ú0 Ë nlim
¯
Æ
nÆ 0
7. a) f ( x ) lim fn ( x ) lim nx enx lim
2
nÆ nÆ nÆ 72
nx
e nx
2
0.
Então, f(x) 0, para todo x.
b) Seja x 1
[0, 1]
n
Ê 1 ˆ
1
1
n◊ 2
1
1
( fn f ) ( x ) ( fn f ) Ê ˆ nÊ ˆ ◊ e Ë n ¯ e n e lim e n 1
Ë n¯
Ë n¯
nÆ Se fn 씮 f uniformemente em [0, 1], dado 0 1, existiria n0 tal que, para todo
1
x [0, 1], n n0 Þ fn ( x ) f ( x ) . Em particular, para x [0, 1] deveríamos
n
1
1
ter fn Ê ˆ f Ê ˆ .
Ë n¯
Ë n¯
1 ˆ
Ê Ê 1ˆ
f Ê ˆ ˜ 1, então fn não converge uniformemente em [0, 1].
Como lim Á fn
Ë n ¯¯
nÆ Ë Ë n ¯
c) Temos
1
1Ê
nxenx
Ú0 Ë nlim
Æ
nxenx
n Æ Ú0
lim
2
2ˆ
¯
dx 0 e
[
1
2
dx Ê ˆ lim enx
Ë 2 ¯ nÆ ] lim ÊË 12 ˆ¯ (e
1
0
Portanto,
1Ê
Ú0 Ë nÆ
lim nxenx
2ˆ
¯
dx lim
Ú
1
nÆ 0
nxenx dx.
2
73
n
nÆ 1) 1
.
2
Exercícios 6.3
1. Temos f ( x ) lim
nÆ 1
nx
x
lim
.
2
1
nx 1 n Æ x 2 x
n
Pela Observação 2 do Teorema 1 desta seção, como cada fn x0 0, mas f ( x ) em ⺢.
nx
é contínua em
nx 2 1
1
não é contínua em x0 0, então fn não converge uniformemente a f
x
2. Veja Exercício 4 da Seção 6.2.
Ï 1 , se x for racional
Ô
3. fn ( x ) Ì n
, n 1.
1
Ô , se x for irracional
Ó n
Para todo x,
lim fn ( x ) 0 f ( x ).
n Æ
As fn são descontínuas em todos os pontos, mas f é contínua.
4. f ( x ) lim nxenx 2
nÆ 1
1
lim
0.
x n Æ e nx 2
1
a)
Ú0 f ( x ) dx 0
1
nxenx
n Æ Ú0
lim
2
1 1
2
dx lim Ê ˆ (2 nx )(enx ) dx Ë
¯
2 0
nÆ Ú
[
]
[
]
1
1
1
2 1
Ê ˆ lim enx
Ê ˆ lim en 1 Ë 2 ¯ nÆ Ë 2 ¯ nÆ 2
0
b) Seja f : [0, 1] 씮 ⺢ dada por f ( x ) lim nxenx 0,
2
nÆ onde cada fn ( x ) nxenx é contínua em [0, 1].
2
Nestas condições, pelo Teorema 2, se fn convergisse uniformemente a f em [0, 1], então
1
1
fn ( x ) dx.
Ú0 f ( x ) dx nlim
Æ Ú0
74
Ú
1
Ú
1
lim fn ( x ) dx lim
fn ( x ) dx (item a)
0 n1
nÆ 0
Æ4
243
Como
f (x)
então, fn não converge uniformemente a f em [0, 1].
5. Seja fn ( x ) n2 x 2
. Temos
1 n2 x 2
f ( x ) lim fn ( x ) lim
nÆ nÆ n2 x 2
1, x 0, e f (0) 0.
1 n2 x 2
Observe que f é limitada e descontínua em apenas x 0, logo integrável em [1, 1].
1
Ú1 nÆ
Daí,
lim fn ( x ) dx 1
Ú1dx 2 .
Por outro lado,
lim
nÆ n2 x 2
nx arc tg nx ù1
dx lim ÈÍ
2.
2
2
1 1 n x
n
nÆ Î
ûú1
Ú
1
Portanto,
1
Ú1
f ( x ) dx lim
Ú
1
n Æ 1
fn ( x ) dx.
75
Vamos mostrar que a seqüência de funções fn, n 1, onde fn ( x ) n2 x 2
não
1 n2 x 2
converge uniformemente a f(x) 1 em [1, 1]. Como os gráficos das fn ficam longe do
1
gráfico de f para um x pequeno, seja x n [1, 1].
n
2
2
n x
1
,
Então, como (f fn) (x) 1 2
2
1 n x
1 n2 x 2
temos
1
1
lim ( f fn ) Ê ˆ 0. Ë
¯
n
2
nÆ Portanto, a convergência não é uniforme.
(Se fn convergisse uniformemente em [1, 1], dado 0, existiria n0 tal que para todo
x [1, 1], n n0 Þ f ( x ) fn ( x ) . Em particular, isto seria válido para x xn, e
daí lim ( f fn ) ( x n ) 0, o que contradiz .)
n Æ
6. Seja fn ( x ) 1
sen nx.
n
Temos f ( x ) lim fn ( x ) lim
nÆ nÆ Como sen nx 1, segue que
Tomando n0 tal que
n n0 Þ
1
sen nx 0.
n
1
1
sen nx .
n
n
1
(n0 só depende de ), resulta
n0
1
sen nx para todo x real.
n
Portanto, a seqüência dada converge uniformemente para f(x) 0, pois, para todo 0,
ˆ
Ê 1
existe n0 (que só depende de ) Á
˜ tal que, para todo x ⺢,
¯
Ë n0
n n0 Þ
1
sen nx 0 .
n
1
sen nx,
n
f(x) 0, f (x) 0 e
fn(x) cos nx.
Sejam fn ( x ) 76
Para x 0, lim fn ( x ) lim cos nx não existe.
nÆ nÆ Portanto, não é verdade que para todo x, f ( x ) lim fn ( x ).
nÆ O Teorema 3 exige que fn seja uniformemente convergente, o que não ocorre com a
seqüência fn; logo, o resultado não está em contradição com o teorema citado.
77