matemática * 9º ano

MATEMÁTICA – 9º ANO 2 de setembro de 2016
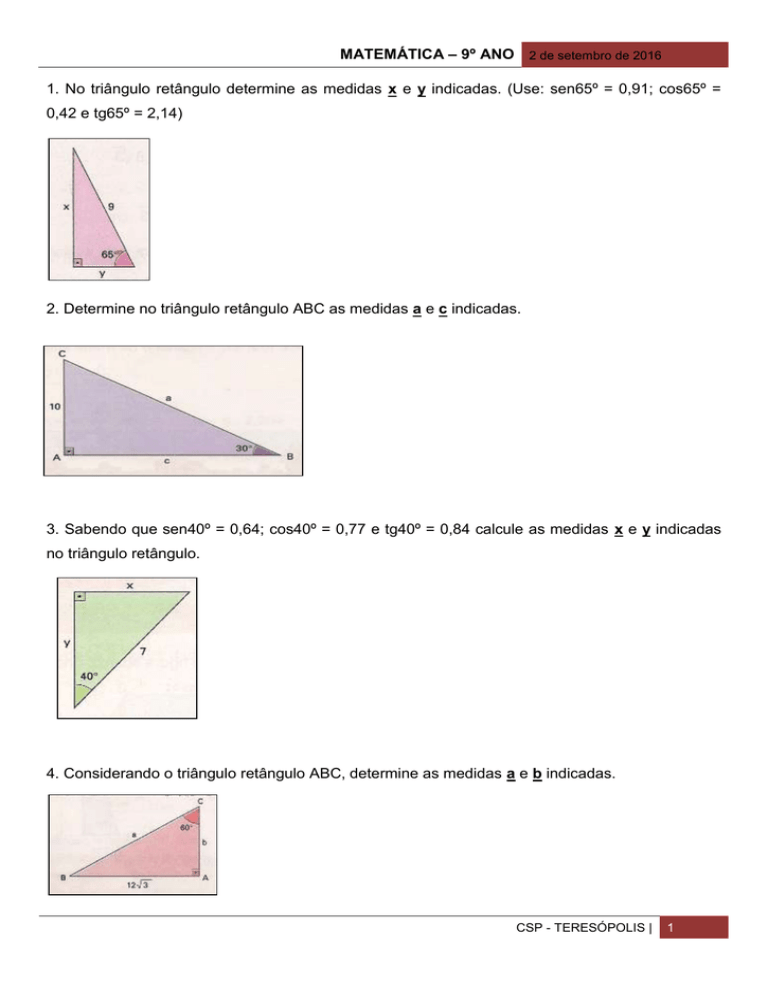
1. No triângulo retângulo determine as medidas x e y indicadas. (Use: sen65º = 0,91; cos65º =
0,42 e tg65º = 2,14)
2. Determine no triângulo retângulo ABC as medidas a e c indicadas.
3. Sabendo que sen40º = 0,64; cos40º = 0,77 e tg40º = 0,84 calcule as medidas x e y indicadas
no triângulo retângulo.
4. Considerando o triângulo retângulo ABC, determine as medidas a e b indicadas.
CSP - TERESÓPOLIS |
1
MATEMÁTICA – 9º ANO 2 de setembro de 2016
5. Em um triângulo retângulo isósceles, cada cateto mede 30cm. Determine a medida da
hipotenusa desse triângulo.
6. A diagonal de um quadrado mede 6 2 cm, conforme nos mostra a figura. Nessas condições,
qual é o perímetro desse quadrado?
7. Uma pipa é presa a um fio esticado que forma um ângulo de 45º com o solo. O comprimento
do fio é 80m. Determine a altura da pipa em relação ao solo. Dado
2 = 1,41
CSP - TERESÓPOLIS |
2
MATEMÁTICA – 9º ANO 2 de setembro de 2016
8. Qual é o comprimento da sombra de uma árvore de 5 m de altura quando o sol está 30º acima
do horizonte? Dado
3 = 1,73
9. Determine a altura do prédio da figura seguinte:
10. Para determinar a altura de um edifício, um observador coloca-se a 30m de distância e assim
o observa segundo um ângulo de 30º, conforme mostra a figura. Calcule a altura do edifício
medida a partir do solo horizontal. Dado
3 = 1,73
CSP - TERESÓPOLIS |
3
MATEMÁTICA – 9º ANO 2 de setembro de 2016
11. Observe a figura e determine:
a) Qual é o comprimento da rampa?
b) Qual é a distância do inicio da rampa ao barranco?
12. A uma distância de 40m, uma torre é vista sob um ângulo  , como mostra a figura.
Determine a altura h da torre se  = 30º.
13. Em um triângulo ABC, retângulo em A, o ângulo B mede 30º e a hipotenusa mede 5cm.
Determine as medidas dos catetos AC e AB desse triângulo.
14. A figura mostra um edifício que tem 15 m de altura, com uma escada colocada a 8 m de sua
base ligada ao topo do edifício. O comprimento dessa escada é de:
a) 12 m.
b) 30 m.
15 m
c) 15 m.
d) 17 m.
8m
 
e) 20 m.
CSP - TERESÓPOLIS |
4
MATEMÁTICA – 9º ANO 2 de setembro de 2016
15. O portão de entrada de uma casa tem 4m de comprimento e 3m de altura. Que comprimento
teria uma trave de madeira que se estendesse do ponto A até o ponto C?
16. Dois navios partem de um mesmo ponto, no mesmo instante, e viajam com velocidades
constante em direções que formam um ângulo reto. Depois de uma hora de viagem, a distância
entre os dois navios é 13 milhas. Se um deles é 7 milhas por hora mais rápido que o outro,
determine a velocidade de cada navio.
17. Durante um incêncio num edifício de apartamentos, os bombeiros utilizaram uma escada
Magirus de 10 m para atingir a janela do apartamento sinistrado. A escada estava colocada a 1m
do chão, sobre um caminhão que se encontrava afastado 6m do edifício. Qual é a altura do
apartamento sinistrado em relação ao chão?
CSP - TERESÓPOLIS |
5
MATEMÁTICA – 9º ANO 2 de setembro de 2016
18. Quantos metros de fio são necessários para “puxar luz” de um poste de 6m de altura até a
caixa de luz que está ao lado da casa e a 8m da base do poste?
19. Uma árvore foi quebrada pelo vento e a partedo tronco que restou em pé forma um ângulo
reto com o solo. Se a altura da árvore antes de se quebrar era de 9m, e sabendo que a ponta da
parte quebrada está a 3m da base da árvore, qual a altura do tronco que restou em pé?
20. Duas circunferências, cujos raios medem 4cm e 6 cm, são tangentes externamente no ponto
F, como mostra a figura.
a) Qual a distância entre os centros dessas circunferências?
b) A reta AB é tangente às duas circunferências nos pontos A e B. Qual é a medida do
segmento de reta AB?
CSP - TERESÓPOLIS |
6