MECÂNICA – TURMA UNP – PARTE 5 LISTA 1

MECÂNICA – TURMA UNP – PARTE 5
LISTA 1:
1. A figura abaixo ilustra uma ferramenta utilizada para apertar ou desapertar determinadas
peças metálicas.
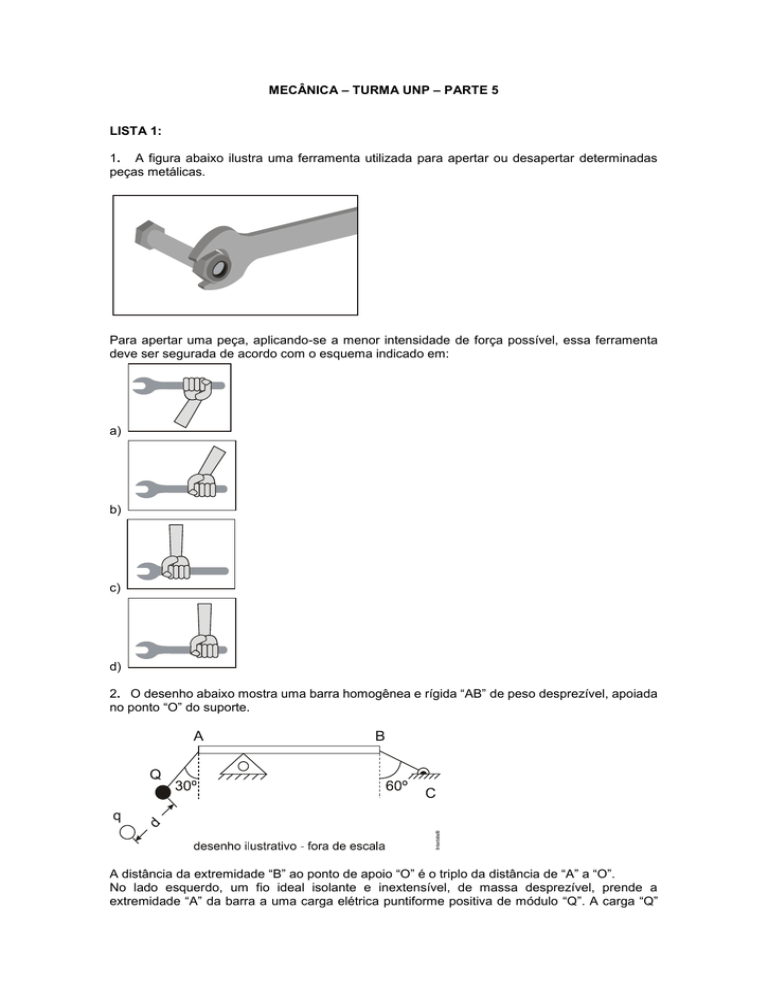
Para apertar uma peça, aplicando-se a menor intensidade de força possível, essa ferramenta
deve ser segurada de acordo com o esquema indicado em:
a)
b)
c)
d)
2. O desenho abaixo mostra uma barra homogênea e rígida “AB” de peso desprezível, apoiada
no ponto “O” do suporte.
A distância da extremidade “B” ao ponto de apoio “O” é o triplo da distância de “A” a “O”.
No lado esquerdo, um fio ideal isolante e inextensível, de massa desprezível, prende a
extremidade “A” da barra a uma carga elétrica puntiforme positiva de módulo “Q”. A carga “Q”
está situada a uma distância “d” de uma outra carga elétrica fixa puntiforme negativa de módulo
“q”.
No lado direito, um fio ideal inextensível e de massa desprezível prende a extremidade “B” da
barra ao ponto “C”.
A intensidade da força de tração no fio “BC”, para que seja mantido o equilíbrio estático da barra
na posição horizontal, é de:
Dados:
sen 30  cos 60  1 2
cos 30  sen 60  3 2
K 0 é a constante eletrostática do meio
K Qq
a) 0
2d2
K Qq
b) 0
4d2
3 K 0Qq
c)
3d2
3 K0Qq
d)
9d2
K Qq
e) 0
d2
3. Um portão maciço e homogêneo de 1,60 m de largura e 1,80 m de comprimento, pesando
800 N, está fixado em um muro por meio das dobradiças “A”, situada a 0,10 m abaixo do topo do
portão, e “B”, situada a 0,10 m de sua parte inferior. A distância entre as dobradiças é de 160 m,
conforme o desenho abaixo.
Elas têm peso e dimensões desprezíveis, e cada dobradiça suporta uma força cujo módulo da
componente
vertical
é
metade
do
peso
do
portão.
Considerando que o portão está em equilíbrio, e que o seu centro de gravidade está localizado
em seu centro geométrico, o módulo da componente horizontal da força em cada dobradiça “A”
e “B” vale, respectivamente:
a) 130 N e 135 N
b) 135 N e 135 N
c) 400 N e 400 N
d) 450 N e 450 N
e) 600 N e 650 N
4. Em um parque de diversões, uma roda gigante gira com velocidade angular constante. De
modo simplificado, pode-se descrever o brinquedo como um disco vertical e as pessoas como
massas puntiformes presas na sua borda. A força peso exerce sobre uma pessoa um torque em
relação ao ponto central do eixo da roda gigante. Sobre esse torque, é correto afirmar-se que:
a) é zero nos pontos mais baixo e mais alto da trajetória.
b) é não nulo e assume um valor máximo no ponto mais alto e um mínimo no ponto mais baixo
da trajetória.
c) é não nulo e assume um valor máximo no ponto mais baixo e um mínimo no ponto mais alto
da trajetória.
d) é não nulo e tem valores iguais no ponto mais baixo e no mais alto da trajetória.
5. Nas figuras (X) e (Y) abaixo, está representado um limpador de janelas trabalhando em um
andaime suspenso pelos cabos 1 e 2, em dois instantes de tempo.
Durante o intervalo de tempo limitado pelas figuras, você observa que o trabalhador caminha
sobre o andaime indo do lado esquerdo, figura (X), para o lado direito, figura (Y).
Assinale a alternativa que preenche corretamente as lacunas da sentença abaixo, na ordem em
que aparecem.
Após o trabalhador ter-se movido para a direita (figura (Y)), podemos afirmar corretamente que,
em relação à situação inicial (figura (X)), a soma das tensões nos cabos 1 e 2 __________, visto
que __________.
a) permanece a mesma - as tensões nos cabos 1 e 2 permanecem as mesmas
b) permanece a mesma - a diminuição da tensão no cabo 1 corresponde a igual aumento na
tensão no cabo 2
c) aumenta - aumenta a tensão no cabo 2 e permanece a mesma tensão no cabo 1
d) aumenta - aumenta a tensão no cabo 1 e permanece a mesma tensão no cabo 2
e) diminui - diminui a tensão no cabo 1 e permanece a mesma tensão no cabo 2
6. O sistema da figura a seguir é composto por uma barra homogênea AB, onde está articulada
em A e pesa 100 N. O objeto P pesa 50 N para que esse sistema permaneça estático. Analise
os seguintes itens:
Informações: sen 30° = 0,5 e cos 30° = 0,87
I. O objeto Q pesa 200 N.
II. A componente horizontal da reação em A é Rx = 170 N.
III. A componente horizontal de Q é Q x = 174 N.
IV. A componente vertical da reação em A é Ry = 50 N.
Estão CORRETAS:
a) I, II, III e IV.
b) I, II e III, apenas.
c) I, III e IV, apenas.
d) II, III e IV, apenas.
e) II e IV, apenas.
7. Uma barra homogênea de peso igual a 50 N está em repouso na horizontal. Ela está apoiada
em seus extremos nos pontos A e B, que estão distanciados de 2 m. Uma esfera Q de peso
80 N é colocada sobre a barra, a uma distância de 40 cm do ponto A, conforme representado
no desenho abaixo:
A intensidade da força de reação do apoio sobre a barra no ponto B é de:
a) 32 N
b) 41 N
c) 75 N
d) 82 N
e) 130 N
8. Retirar a roda de um carro é uma tarefa facilitada por algumas características da ferramenta
utilizada, habitualmente denominada chave de roda. As figuras representam alguns modelos de
chaves de roda:
Em condições usuais, qual desses modelos permite a retirada da roda com mais facilidade?
a) 1, em função de o momento da força ser menor.
b) 1, em função da ação de um binário de forças.
c) 2, em função de o braço da força aplicada ser maior.
d) 3, em função de o braço da força aplicada poder variar.
e) 3, em função de o momento da força produzida ser maior.
Gabarito:
Resposta
[D]
da
questão
1:
Quanto maior o braço da alavanca (distância da linha de ação da força ao apoio), menor a
intensidade da força para se obter o mesmo torque.
Resposta
[C]
da
questão
2:
Comentário: O enunciado pede a intensidade da força de tração no fio. Para que haja equilíbrio
da barra, o fio ligado à extremidade A deve estar tracionado. Para tal, as cargas elétricas das
pequenas esferas devem ser de sinais opostos. Se na expressão da força elétrica as cargas não
forem colocadas em módulo, a intensidade da tração será negativa, o que é um absurdo.
A intensidade da força de tração no fio ligado na extremidade A é à da força elétrica entre as
cargas.
A figura ilustra a situação:
Como a barra está em equilíbrio, o somatório dos momentos das forças em torno do ponto E é
nulo. Seja FB a intensidade da força de tração no fio “BC”
MFC
Ay
 MFC
By
 FAy D  FBy 3D  FA cos 30  3 FB cos 60 
K 0 | Q || q | 3
1
 3 FB
2
2
2
d
FB 

3 K 0 | Q || q |
.
3 d2
Resposta
[C]
da
questão
3:
Se o portão está em equilíbrio, o somatório dos momentos em relação a qualquer ponto é nulo.
A figura mostra as componentes horizontais das forças atuantes nas dobradiças.
Em relação ao ponto B, temos:
B
MB
 MP
 FA 1,6  800  0,8 
F
A
 FA 
6.400
 400 N.
1,6
 FA  FB  400 N.
Resposta
[A]
da
questão
4:
A figura mostra que nos pontos mais baixo e mais alto a linha de ação do peso passa pelo ponto
central (C); portanto, nesses pontos, em relação ao ponto central da roda, o torque da força peso
é zero.
Resposta
[B]
da
questão
Como o andaime permanece em equilíbrio, podemos afirmar que
Analisando
F  0 :
F  0 e M  0 .
5:
P : peso do limpador;
P ' : peso do andaime;
T : tensão no cabo 1;
T ' : tensão no cabo 2.
F  0  T  T ' P  P'  0  T  T ' P  P'  0  T  T '  P  P'
P  P'  cons tan te  T  T '  cons tan te
Condição que é satisfeita pelas alternativas [A] e [B] apenas.
Como T  T '  cons tan te , podemos concluir que o aumento da tensão no cabo 2 corresponde
à mesma diminuição da tensão no cabo 1, condição esta satisfeita apenas pela alternativa [B].
Resposta
[C]
da
questão
6:
O ponto B é tracionado por duas forças: uma vertical igual ao peso P e outra inclinada igual ao
peso Q. A figura abaixo mostra as forças atuando na barra já devidamente decompostas.
O somatório dos momentos das forças em relação a “A” deve ser nulo. Portanto:
Qsen30.AB  PxAB  Pbarra x
Qx0,5  50  100x
AB
2
1
 Q  200N
2
A resultante horizontal deve ser nula. Portanto:
Rx  Qcos30  200x0,87  174N
A resultante vertical deve ser nula. Portanto:
Ry  Qsen30  P  Pbarra  R y  174x0,5  50  100  R y  150  87  63N
Resposta
[B]
da
questão
7:
Desenhando todas as forças que atuam na barra, bem como a localização do ponto O, e
adotando como positivo o sentido horário de rotação, teremos:
Sendo:
Pb : peso da barra;
PQ : peso da esfera;
NA : Força normal trocada com o apoio A;
NB : Força normal trocada com o apoio B.
Considerando que a soma dos momentos de todas as forças, em relação ao ponto O, é igual à
zero (condição de equilíbrio), teremos:
(m)o  0

(mNB )o  (mPb )o  (mPQ )o  (mNA )o  0
NB .2  Pb .1  PQ .0,4  NA .0  0
NB .2  50.1  80.0,4  0  0
NB .2  50  32  0
NB .2  82  0
NB  41N
Resposta
[B]
da
questão
8:
Para forças de mesma intensidade (F), aplicadas perpendicularmente nas extremidades das
alavancas, para os três modelos, 1, 2 e 3, temos os respectivos momentos:
M1  F  40

M2  F  30
M  F  25
 3
 M1  M2  M3 .
LISTA 2:
1. Considere as proposições relacionadas aos fluidos hidrostáticos.
I. A pressão diminui com a altitude acima do nível do mar e aumenta com a profundidade abaixo
da interface ar-água.
II. O elevador hidráulico é baseado no Princípio de Pascal.
III. Sabendo-se que a densidade do gelo, do óleo e da água são iguais a
0,92 g / cm3 ; 0,80 g / cm3 e 1,0 g / cm3 , respectivamente, pode-se afirmar que o gelo afunda no
óleo e flutua na água.
IV. O peso aparente de um corpo completamente imerso é menor que o peso real, devido à ação
da força de empuxo, exercida pelo líquido sobre o corpo, de cima para baixo.
Assinale a alternativa correta.
a) Somente as afirmativas I, II e III são verdadeiras.
b) Somente as afirmativas II e IV são verdadeiras.
c) Somente as afirmativas I e II são verdadeiras.
d) Somente as afirmativas I, III e IV são verdadeiras.
e) Todas as afirmativas são verdadeiras.
2. Considere um cubo imerso em água, conforme a figura a seguir.
No ponto destacado de uma das faces desse cubo, há uma força devido à pressão hidrostática
exercida pela água. Assinale o vetor que melhor representa essa força.
a) FI
b) FII
c) FIII
d) FIV
3. Aquecedores de passagem são acionados pela passagem da água no seu interior, ou seja,
ligam quando a torneira é aberta. O manual de instalação de um aquecedor deste tipo informa
que “a pressão mínima necessária para o correto funcionamento do equipamento é equivalente
a 10m de coluna de água”.
Levando-se em conta que a massa específica da água é 1000kg/m 3 e a aceleração da gravidade
no local é aproximadamente 10m/s2, a informação se refere à pressão hidrostática, em pascais,
de:
a) 1,0  106
b) 1,0  105
c) 1,0  10 4
d) 1,0  103
e) 1,0  102
4. Com o objetivo de encontrar grande quantidade de seres vivos nas profundezas do mar,
pesquisadores utilizando um submarino chegaram até a profundidade de 3.600 m no Platô de
São Paulo. A pressão interna no submarino foi mantida igual à pressão atmosférica ao nível do
mar. Considere que a pressão atmosférica ao nível do mar é de 1,0  105 N / m2 , a aceleração
da gravidade é 10 m/s2 e que a densidade da água seja constante e igual a 1,0  103 kg / m3 .
Com base nos conceitos de hidrostática, assinale a alternativa que indica quantas vezes a
pressão externa da água sobre o submarino, naquela profundidade, é maior que a pressão no
seu interior, se o submarino repousa no fundo do platô.
a) 10.
b) 36.
c) 361.
d) 3610.
e) 72000.
5. Um passeio de balão é uma das atrações para quem visita a Capadócia, na Turquia.
Os balões utilizados para esse tipo de passeio possuem um grande bocal por onde uma forte
chama aquece o ar do interior do balão. Abaixo do bocal, está presa a gôndola onde os turistas
se instalam para fazer um passeio inesquecível.
Esses balões ganham altitude porque:
a) o ar aquecido é menos denso que o ar atmosférico.
b) a queima do combustível gera oxigênio, que é mais leve que o ar.
c) a pressão interna torna-se maior que a pressão externa, ao serem inflados.
d) o gás liberado na queima aumenta a inércia sobre a superfície do balão.
e) o calor da chama é dirigido para baixo e, como reação, o balão é empurrado para cima.
6. Um bloco de volume V = 0,25 m 3 e massa 0,05 kg está preso a um fio ideal e completamente
imerso em um líquido de densidade ρ  400 kg / m3 contido em uma caixa selada, conforme
ilustra a figura.
Sabendo-se que a tensão no fio nessa situação é igual a 89,5 N, determine o módulo da reação
normal da superfície superior da caixa sobre o bloco.
a) 0,0 N
b) 89,0 N
c) 910,0 N
d) 910,5 N
e) 1000,0 N
7.
Um bloco de madeira impermeável, de massa M e dimensões 2  3  3 cm3 , é inserido muito
lentamente na água de um balde, até a condição de equilíbrio, com metade de seu volume
submersa. A água que vaza do balde é coletada em um copo e tem massa m. A figura ilustra as
situações inicial e final; em ambos os casos, o balde encontra-se cheio de água até sua
capacidade máxima. A relação entre as massas m e M é tal que:
a) m = M/3
b) m = M/2
c) m = M
d) m = 2M
e) m = 3M
8. Um cubo maciço e homogêneo, com 40 cm de aresta, está em equilíbrio estático flutuando
em uma piscina, com parte de seu volume submerso, conforme desenho abaixo.
Sabendo-se que a densidade da água é igual a 1 g/cm3 e a distância entre o fundo do cubo (face
totalmente submersa) e a superfície da água é de 32 cm, então a densidade do cubo:
a) 0,20 g/cm3
b) 0,40 g/cm3
c) 0,60 g/cm3
d) 0,70 g/cm3
e) 0,80 g/cm3
9. Os precursores no estudo da Hidrostática propuseram princípios que têm uma diversidade
de aplicações em inúmeros “aparelhos” que simplificam as atividades extenuantes e penosas
das pessoas, diminuindo muito o esforço físico, como também encontraram situações que
evidenciam os efeitos da pressão atmosférica. A seguir, são apresentadas as situaçõesproblema que ilustram aplicações de alguns dos princípios da Hidrostática.
Situação I – Um sistema
hidráulico de freios de alguns
carros, em condições adequadas,
quando um motorista aciona o
freio de um carro, este para após
alguns segundos, como mostra
figura acima.
Situação II – Os pedreiros,
para nivelar dois pontos em
uma obra, costumam usar
uma mangueira transparente,
cheia de água. Observe a
figura acima, que mostra
como os pedreiros usam uma
mangueira com água para
nivelar os azulejos nas
paredes.
Situação III – Ao sugar na
extremidade e de um canudo,
você provoca uma redução na
pressão do ar em seu interior. A
pressão atmosférica, atuando na
superfície do líquido, faz com
que ele suba no canudinho.
Assinale a alternativa que corresponde, respectivamente, às aplicações dos princípios e do
experimento formulados por:
a) Arquimedes (Situação I), Pascal (Situação II) e Arquimedes (Situação III)
b) Pascal (Situação I), Arquimedes (Situação II) e Stevin (Situação III)
c) Stevin (Situação I), Torricelli (Situação II) e Pascal (Situação III)
d) Pascal (Situação I), Stevin (Situação II) e Torricelli (Situação III)
e) Stevin (Situação I), Arquimedes (Situação II) e Torricelli (Situação III).
10.
Em 1643, o físico italiano Evangelista Torricelli (1608-1647) realizou sua famosa
experiência, medindo a pressão atmosférica por meio de uma coluna de mercúrio, inventando,
assim, o barômetro. Após esta descoberta, suponha que foram muitos os curiosos que fizeram
várias medidas de pressão atmosférica.
Com base na experiência de Torricelli, pode-se afirmar que o maior valor para altura da coluna
de mercúrio foi encontrado:
a) no Pico do Jabre, ponto culminante do estado da Paraíba, no município de Matureia.
b) no alto de uma montanha a 1500 metros de altitude.
c) no 10° andar de um prédio em construção na cidade de Campina Grande.
d) numa bonita casa de veraneio em João Pessoa, no litoral paraibano.
e) no alto do Monte Everest, o ponto culminante da Terra.
11. Para realizar um experimento com uma garrafa PET cheia de água, perfurou-se a lateral da
garrafa em três posições a diferentes alturas. Com a garrafa tampada, a água não vazou por
nenhum dos orifícios, e, com a garrafa destampada, observou-se o escoamento da água,
conforme ilustrado na figura.
Como a pressão atmosférica interfere no escoamento da água, nas situações com a garrafa
tampada e destampada, respectivamente?
a) Impede a saída de água, por ser maior que a pressão interna; não muda a velocidade de
escoamento, que só depende da pressão da coluna de água.
b) Impede a saída de água, por ser maior que a pressão interna; altera a velocidade de
escoamento, que é proporcional à pressão atmosférica na altura do furo.
c) Impede a entrada de ar, por ser menor que a pressão interna; altera a velocidade de
escoamento, que é proporcional à pressão atmosférica na altura do furo.
d) Impede a saída de água, por ser maior que a pressão interna; regula a velocidade de
escoamento, que só depende da pressão atmosférica.
e) Impede a entrada de ar, por ser menor que a pressão interna; não muda a velocidade de
escoamento, que só depende da pressão da coluna de água.
12. Para oferecer acessibilidade aos portadores de dificuldade de locomoção, é utilizado, em
ônibus e automóveis, o elevador hidráulico. Nesse dispositivo é usada uma bomba elétrica, para
forçar um fluido a passar de uma tubulação estreita para outra mais larga, e dessa forma acionar
um pistão que movimenta a plataforma. Considere um elevador hidráulico cuja área da cabeça
do pistão seja cinco vezes maior do que a área da tubulação que sai da bomba. Desprezando o
atrito e considerando uma aceleração gravitacional de 10m/s 2, deseja-se elevar uma pessoa de
65kg em uma cadeira de rodas de 15kg sobre a plataforma de 20kg.
Qual deve ser a força exercida pelo motor da bomba sobre o fluido, para que o cadeirante seja
elevado com velocidade constante?
a) 20N
b) 100N
c) 200N
d) 1000N
e) 5000N
Gabarito:
Resposta
[A]
da
questão
1:
Justificando a falsa:
[I] Verdadeira.
[II] Verdadeira.
[III] Verdadeira.
[IV] Falsa. O peso aparente de um corpo completamente imerso é menor que o peso real, devido
à ação da força de empuxo, exercida pelo líquido sobre o corpo, de baixo para cima.
Resposta
[A]
da
questão
2:
A força que provoca pressão é perpendicular á área de aplicação.
Resposta
[B]
da
questão
3:
Observação: de acordo com o Sistema Internacional de Unidades, o plural de grandezas
provenientes de nomes próprios é feito apenas com o acréscimo de s. Assim, o termo correto e
pascals e não pascais.
p  d g h  103  10  10  p  105 pascals.
Resposta
[C]
da
questão
4:
Dados: pint = pint = 105 N/m2; h = 3.600 m; g = 10 m/s2.
pext  pint  d g h  105  103  10  3.600  105  360  105  Pext  361 105 
pext  361 pint .
Resposta
[A]
da
questão
5:
O ar aquecido dentro do balão se expande, tornando-se menos denso que o ar externo. Assim,
o peso do balão torna-se menor que o empuxo, fazendo que ele suba.
Resposta
[C]
da
questão
6:
Observação: o termo tensão tem dimensão de força/área. Portanto, no enunciado, deveria
aparecer o termo tração.
Dados: m  0,05kg; V  0,25m3 ; ρ  400 kg/m3 ; g  10 m/s 2; T  89,5N.
A figura mostra as forças agindo no bloco.
Do equilíbrio:
FN  T  P  E
 F  ρg V  mg T 
FN  400  10  0,25  0,05  10  89,5 
FN  910 N.
Resposta
[C]
da
questão
7:
No equilíbrio, o empuxo sobre o bloco tem a mesma intensidade do peso do bloco.
A água que extravasa cai no copo, portanto o volume deslocado de água é igual ao volume que
está no copo.
m  dágua Vdesloc

E  dágua Vdesloc g  E  P  dágua Vdesloc g  M g  dágua Vdesloc  M 

P  M g
m  M.
Resposta
[E]
da
questão
8:
Se o corpo está em repouso, o peso e o empuxo têm a mesma intensidade:
dcubo vimerso
P  E  dcubo Vcubo g  dágua Vimerso g 


dágua
Vcubo
dcubo Abase himersa

dágua
Abase Hcubo

dcubo 32

1
40

dcubo  0,8 g /cm3 .
Resposta
[D]
da
questão
9:
- Situação I – aplicação do freio hidráulico, baseado no princípio de Pascal: qualquer acréscimo
de pressão efetuado num ponto de um líquido em repouso é transmitido integralmente aos
demais pontos desse líquido.
- Situação II – aplicação do princípio de Stevin: pontos de um mesmo líquido que estão na
mesma horizontal estão sob mesma pressão.
- Situação III – Princípio de Torricelli: (já explicado no texto)
Resposta
[D]
da
questão
10:
O maior valor da coluna de mercúrio foi encontrado no local onde a pressão atmosférica é maior,
ou seja, ao nível do mar.
Resposta
[A]
da
questão
11:
Para que a pressão interior fosse maior que a pressão atmosférica, a coluna de água deveria ter
mais de 10 m. Logo, a água não sairá com a garrafa fechada.
Abrindo-se a garrafa, a pressão no orifício aumenta com a profundidade em relação à superfície
da água, acarretando maior velocidade na saída.
Resposta
da
questão
12:
[C]
O módulo do peso (P) do conjunto a ser elevado é:


P  mpessoa  mcad  mplat g  P   65  15  20 10  1.000 N.
Como a velocidade é constante, aplicando a expressão do Princípio de Pascal:
Fmotor
Fmotor
P
1.000




A tub
Apistão
A tub
5  A tub
Fmotor  200 N.
LISTA 3:
1. Considere dois satélites artificiais S e T em torno da Terra. S descreve uma órbita elíptica
com semieixo maior a, e T, uma órbita circular de raio a, com os respectivos vetores posição r S
e r T com origem no centro da Terra. É correto afirmar que:
a) para o mesmo intervalo de tempo, a área varrida por r S é igual à varrida por r T .
b) para o mesmo intervalo de tempo, a área varrida por r S é maior que a varrida por r T .
c) o período de translação de S é igual ao de T.
d) o período de translação de S é maior que o de T.
e) se S e T têm a mesma massa, então a energia mecânica de S é maior que a de T.
2. Após o lançamento do primeiro satélite artificial Sputnik I pela antiga União Soviética (Rússia)
em 1957, muita coisa mudou na exploração espacial. Hoje temos uma Estação Espacial
internacional (ISS) que orbita a Terra em uma órbita de raio aproximadamente 400km. A ISS
realiza sempre a mesma órbita ao redor da Terra, porém, não passa pelo mesmo ponto fixo na
Terra todas as vezes que completa sua trajetória. Isso acontece porque a Terra possui seu
movimento de rotação, ou seja, quando a ISS finaliza sua órbita, a Terra girou, posicionando-se
em outro local sob a Estação Espacial.
Considere os conhecimentos de gravitação e o exposto acima e assinale a alternativa correta
que completa as lacunas das frases a seguir.
A Estação Espacial Internacional ____________ como um satélite geoestacionário. Como está
em órbita ao redor da Terra pode-se afirmar que a força gravitacional __________ sobre ela.
a) não se comporta - não age
b) não se comporta - age
c) se comporta - não age
d) se comporta - age
3.
No poema “O que se afasta”, o eu poético de Sísifo desce a montanha afirma, por
comparação, que as coisas perdem seu peso e gravidade, percepção que está relacionada ao
envelhecimento do homem:
“De repente você começa a se despedir
das pessoas, paisagens e objetos
como se um trem
— fosse se afastando (...)”.
Aproveitando o ensejo literário, imagine um objeto próximo à superfície da Terra e uma situação
hipotética, porém sem abrir mão de seus importantes conhecimentos de Física.
Supondo a possibilidade de haver alteração no raio e/ou na massa da Terra, assinale a opção
que traz uma hipótese que justificaria a diminuição do peso desse objeto, que se mantém próximo
à superfície do Planeta:
a) diminuição do raio da Terra e manutenção de sua massa.
b) aumento da massa da Terra e manutenção de seu raio.
c) aumento do raio da Terra e diminuição de sua massa, na mesma proporção.
d) diminuição do raio da Terra e aumento de sua massa, na mesma proporção.
4. Em 6 de agosto de 2012, o jipe “Curiosity" pousou em Marte. Em um dos mais espetaculares
empreendimentos da era espacial, o veículo foi colocado na superfície do planeta vermelho com
muita precisão. Diferentemente das missões anteriores, nesta, depois da usual descida balística
na atmosfera do planeta e da diminuição da velocidade provocada por um enorme paraquedas,
o veículo de quase 900 kg de massa, a partir de 20 m de altura, foi suave e lentamente baixado
até o solo, suspenso por três cabos, por um tipo de guindaste voador estabilizado no ar por meio
de 4 pares de foguetes direcionais. A ilustração abaixo representa o evento.
O cabo ondulado que aparece na figura serve apenas para comunicação e transmissão de
energia entre os módulos.
Considerando as seguintes razões: massa da Terra/massa de Marte ~ 10 e raio médio da
Terra/raio médio de Marte ~ 2, a comparação com descida similar, realizada na superfície
terrestre, resulta que a razão correta entre a tensão em cada cabo de suspensão do jipe em
Marte e na Terra (TM/TT) é, aproximadamente, de:
a) 0,1.
b) 0,2.
c) 0,4.
d) 2,5.
e) 5,0.
5. A terceira Lei de Kepler estabelece uma proporção direta entre o quadrado do período de
translação de um planeta em torno do sol e o cubo do raio médio da órbita. A partir dessa Lei, é
correto afirmar que:
a) o movimento de translação, em uma órbita específica, é mais rápido quando o planeta está
mais próximo do sol.
b) a velocidade média de translação é maior para os planetas em órbitas mais distantes do Sol.
c) as áreas varridas pelo raio orbital são iguais durante o movimento de translação.
d) as posições do sol estão nos focos das órbitas de translação elípticas.
6. A massa da Terra é de 6,0  1024 kg , e a de Netuno é de 1,0  1026 kg . A distância média da
Terra ao Sol é de 1,5  1011 m , e a de Netuno ao Sol é de 4,5  1012 m . A razão entre as forças
de interação Sol-Terra e Sol-Netuno, nessa ordem, é mais próxima de:
a) 0,05.
b) 0,5.
c) 5.
d) 50.
e) 500.
7. Dois satélites, denominados de SA e SB, estão orbitando um planeta P. Os dois satélites são
esféricos e possuem tamanhos e massas iguais. O satélite S B possui uma órbita perfeitamente
circular e o satélite SA uma órbita elíptica, conforme mostra a figura abaixo.
Em relação ao movimento desses dois satélites, ao longo de suas respectivas órbitas, considere
as seguintes afirmativas:
1. Os módulos da força gravitacional entre o satélite SA e o planeta P e entre o satélite SB e o
planeta P são constantes.
2. A energia potencial gravitacional entre o satélite SA e o satélite SB é variável.
3. A energia cinética e a velocidade angular são constantes para ambos os satélites.
Assinale a alternativa correta.
a) Somente a afirmativa 1 é verdadeira.
b) Somente a afirmativa 2 é verdadeira.
c) Somente a afirmativa 3 é verdadeira.
d) Somente as afirmativas 1 e 2 são verdadeiras.
e) Somente as afirmativas 2 e 3 são verdadeiras.
8. A Lei da Gravitação Universal, de Isaac Newton, estabelece a intensidade da força de atração
entre duas massas. Ela é representada pela expressão:
mm
FG 1 2
d2
onde m1 e m2 correspondem às massas dos corpos, d à distância entre eles, G à constante
universal da gravitação e F à força que um corpo exerce sobre o outro.
O esquema representa as trajetórias circulares de cinco satélites, de mesma massa, orbitando a
Terra.
Qual gráfico expressa as intensidades das forças que a Terra exerce sobre cada satélite em
função do tempo?
a)
b)
c)
d)
e)
9. Muitos ainda acreditam que como a órbita da Terra em torno do Sol é uma elipse e o Sol não
está no centro dessa elipse, as estações do ano ocorrem porque a Terra ora fica mais próxima
do Sol, ora mais afastada. Se isso fosse verdade, como se explica o fato de o Natal ocorrer numa
época fria (até nevar) nos países do hemisfério norte e no Brasil ocorrer numa época de muito
calor? Será que metade da Terra está mais próxima do Sol e a outra metade está mais afastada?
Isso não faz sentido. A existência das estações do ano é mais bem explicada:
a) pelo fato de o eixo imaginário de rotação da Terra ser perpendicular ao plano de sua órbita ao
redor do Sol.
b) pelo fato de em certas épocas do ano a velocidade de translação da Terra ao redor do Sol ser
maior do que em outras épocas.
c) pela inclinação do eixo imaginário de rotação da Terra em relação ao plano de sua órbita ao
redor do Sol.
d) pela velocidade de rotação da Terra em relação ao seu eixo imaginário não ser constante.
e) pela presença da Lua em órbita ao redor da Terra, exercendo influência no período de
translação da Terra ao redor do Sol.
10. A tabela a seguir resume alguns dados sobre dois satélites de Júpiter.
Nome
Diâmetro
aproximado (km)
Raio médio da órbita em relação
ao centro de Júpiter (km)
Io
3,64  103
4,20  105
Europa
3,14  103
6,72  105
Sabendo-se que o período orbital de Io é de aproximadamente 1,8 dia terrestre, pode-se afirmar
que o período orbital de Europa expresso em dia(s) terrestre(s), é um valor mais próximo de:
a) 0,90
b) 1,50
c) 3,60
d) 7,20
Gabarito:
Resposta
[C]
da
questão
1:
De acordo com a 3ª lei de Kepler, para todos os planetas de um mesmo sistema solar, ou para
todos os satélites de um mesmo planeta, a relação entre o período de translação (T) e raio médio
da órbita (rm) é dada pela expressão:
T2
 k (constante), sendo rm igual à medida do semieixo maior para órbitas elípticas, e, igual ao
3
rm
raio, para órbitas circulares. Assim, como o semieixo maior da órbita de S é igual ao raio da órbita
de T, os dois satélites têm o mesmo período de translação.
Resposta
[B]
da
questão
2:
Se a Estação Espacial Internacional não está fixa sobre um mesmo ponto da Terra ela não se
comporta como geoestacionário. Se ela está em órbita, a força gravitacional age sobre ela
Resposta
[C]
da
questão
3:
Para diminuir o peso desse objeto, deveríamos diminuir o campo gravitacional terrestre (g).
Analisando a expressão, vejamos o que aconteceria se aumentássemos o raio e diminuíssemos
a massa na mesma proporção. Sendo k esse fator, temos:
GM

g  2
R

G M R2
g'
g

M



 g' 

3
G 
2
g k R GM
k3

GM
k

 g' 
g' 
k 3 R2

 k R 2
O peso diminuiria, ficando dividido pelo cubo desse fator.
Resposta
[C]
da
Desenhando as forças que atuam no jipe:
P : peso do jipe; T : tensão em um dos cabos.
questão
4:
Analisando os vetores velocidade ( V ), força resultante ( R ) e aceleração ( a ) do jipe, sendo que
ele desce em movimento retardado:
m.a  m.g
, sendo a
3
aceleração (a) igual em todos os casos, pois temos os mesmos 20m para parar o jipe com a
mesma velocidade inicial.
Aplicando a Segunda Lei de Newton: R  m.a  3T  P  m.a  T 
Marte: TM 
m.a  m.gM
3
Terra: TT 
m.a  m.gT
3
Lembrando que g 
gM 
G.MM
rM2
e gT 
G.M
, onde M é a massa do planeta e r o raio do planeta.
r2
G.MT
rT2
Como MT  10MM e rT  2rM , teremos:
G.MT
G.10MM
G.10MM
gT 
 gT 
 gT 
 gT  2,5.gM
2
2
rT
(2rM )
4rM2
Lembrado que: TT 
m.a  m.gT
m.a  m.gM
e TM 
3
3
m.a  m.gM
TM
T
a  gM
3

 M 
m.a  m.gT
TT
TT a  gT
3
Aplicando gT  2,5.gM :
Resposta
[A]
TM a  gM
T
a  gM
T

 M 
 M  0,4
TT a  gT
TT a  2,5.gM
TT
da
questão
5:
GM
, sendo r o raio da órbita, G a
r
constante de gravitação universal e M a massa do Sol. Assim, a justificativa para a resposta dada
é dada pela Lei de Newton da Gravitação, e não pela terceira Lei da Kepler, embora, lógico, uma
leve à outra.
A velocidade de translação de um planeta é dada por: v 
A terceira Lei de Kepler, T2  k r 3, é mais adequada quando se comparam os períodos de
translação entre dois planetas.
Resposta
da
questão
6:
[D]
Dados: mT  6  1024 kg; mT  1 1026 kg; dTS  1,5  1011m; dNS  4,5  1012 m.
Da lei de Newton da Gravitação:

G M mT
FST 
 dTS 2

FST G M mT
 dNS 2
 



2
FSN
G M mN
dTS 
F  G M mN

2
 SN
 dNS 

d 
FST mT

  NS 
FSN mN
 dTS 

2
2

 4,5  1012 
FST 6  1024


  6  10 2  9  102 
 1,5  1011 
FSN 1 1026


FST
 54.
FSN
Resposta
[B]
da
questão
1. Incorreta. De acordo com a lei de Newton da Gravitação: F 
7:
GMm
, sendo d a distância
d2
entre o planeta e o satélite. Para o satélite A, a distância é variável, então a força gravitacional
tem intensidade variável.
G mA mB
2. Correta. A energia potencial gravitacional entre os dois satélites é: Epot  
. Se a
dAB
distância dAB é variável, a energia potencial gravitacional do sistema formado por SA e SB também
é variável.
3. Incorreta. Pela expressão mostrada no item anterior, a energia potencial gravitacional entre o
planeta e o satélite SA é variável. Tratando-se de sistema conservativo, consequentemente, a
energia cinética do satélite SA é variável, aumentando à medida que o satélite aproxima-se do
planeta.
Resposta
[B]
da
questão
8:
A intensidade da força de atração gravitacional é inversamente proporcional ao quadrado da
distância entre a Terra e o satélite. Como as órbitas são circulares, a distância para cada satélite
é constante, sendo também constante a intensidade da força gravitacional sobre cada um. Como
as massas são iguais, o satélite mais distante sofre força de menor intensidade.
Assim: FA < FB < FC < FD < FE.
Resposta
[C]
da
questão
9:
A existência das estações é devido à inclinação do eixo de rotação da Terra em relação ao plano
da eclíptica.
Resposta
[C]
da
questão
T2
10:
 K , em que T representa
r3
o período orbital, r o raio médio orbital e K uma constante de proporcionalidade.
Matematicamente, a terceira lei de Kepler pode ser expressa por:
Como os satélites Io e Europa giram em torno do mesmo centro, que é Júpiter, devido à força
gravitacional trocada com o planeta, podemos escrever que:
T2Europa
r 3Europa

T2Io
r 3Io

T2Europa
5 3
(6,72.10 )
TEuropa  3,64 dias terrestres.

(1,8)2
5 3
(4,20.10 )
 T2Europa  13,27