Geometria Plana - Claudio Cabral

GEOMETRIA PLANA
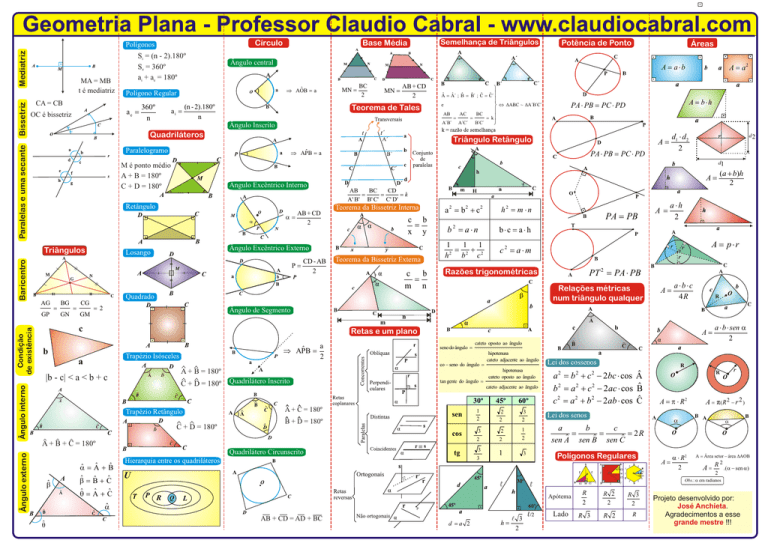
GEOMETRIA PLANA
Mediatriz
Bissetriz
Paralelas e uma secante
Si = (n - 2).180º
Se = 360º
ai + ae = 180º
ae 
OC é bissetriz
360º
n
MN 
(n - 2).180º
n
BC
2
MN 
AB + CD
2


  ABC ~ A´B´C´



 k
A´B´ A´C´ B´C´

AB
BG

CG
d2
d1  d2
2
A
PA  PB  PC  PD
Retângulo
Teorema da Bissetriz Interna
2
2
2
2
h  m n
a  b c
AB + CD
c b
a
2

α α
x

y
Ângulo Excêntrico Externo
CD - AB
2
Teorema da Bissetriz Externa
c b

m n
α
α
b2  an
bc  a h
1
1 1


h2 b2 c2
c2  am
PA  PB
A
ah
2
A  pr
PT 2  PA  PB
Razões trigonométricas

 2
Relações métricas
num triângulo qualquer
A
abc
4R
Ângulo de Segmento
GM
Condição
de existência
α
Retas e um plano
 AP̂B 
Trapézio Isósceles
D
|b - c| < a < b + c
Trapézio Retângulo
D
C + D = 180º
hipotenusa
cateto adjacente ao ângulo
co  seno do ângulo 
α
hipotenusa
cateto oposto ao ângulo
Quadrilátero Inscrito
tan gente do ângulo 
cateto adjacente ao ângulo
A + C = 180º
30º
45º
60º
sen
1
2
2
2
3
2
cos
3
2
1
2
2
2
3
3
1
3
B + D = 180º
α

Ângulo externo
Quadrilátero Circunscrito
α
tg
Hierarquia entre os quadriláteros
Lei dos cossenos
a 2  b 2  c 2  2bc  cos
b 2  a 2  c 2  2 ac  cos
c 2  a 2  b 2  2 ab  cos

A

B
C
A    R2
Lei dos senos
Polígonos Regulares
A  π( R 2  r 2 )
a
a
a
a
a
b
c


 2R
sen A sen B sen C
A
  R2
2
A  Área setor  área AOB
2
A  R .(  sen )
2
Obs.:  em radianos
α
ˆ  Â  Ĉ
Apótema
R
2
R 2
2
R 3
2
Lado
R 3
R 2
R
̂
AB + CD = AD + BC
̂
a  b  sen 
2
seno do ângulo 
A + B + C = 180º
ˆ  Â  B̂
ˆ  B̂  Ĉ
α
cateto oposto ao ângulo
a
2
A + B = 180º
C + D = 180º
A
α
̂
(a  b)h
2
AB
BC
CD


k
A' B' B' C' C' D'
Quadrado
GN
A  bh
PA  PB  PC  PD
BC
A
Ângulo Excêntrico Interno
Losango
Baricentro
AC
d1
P

A  a2
  ´ ; B̂  B̂´ ; Ĉ  Ĉ´ 
 AP̂B  a
M é ponto médio
A + B = 180º
C + D = 180º
GP
Áreas
Triângulo Retângulo
Paralelogramo
AG
Potência de Ponto
e
Teorema de Tales
Ângulo Inscrito
Triângulos
GEOMETRIA PLANA
A  ab
Quadriláteros
Ângulos colaterais internos: c e f, d e e;
Ângulos colaterais externos: b e g, a e h;
Ângulos alternos internos: d e f, c e e;
Ângulos alternos externos: a e g, b e h;
Ângulos correspondentes: a e e, b e f, c e g, d e
h.
GEOMETRIA PLANA
Semelhança de Triângulos
Base Média
 AÔB  a
ai 
GEOMETRIA PLANA
Ângulo central
Polígono Regular
CA = CB
GEOMETRIA PLANA
Círculo
Polígonos
MA = MB
t é mediatriz
GEOMETRIA PLANA
α
d a 2
h
 3
2
Projeto desenvolvido por:
José Anchieta.
Agradecimentos a esse
grande mestre !!!