Lista 3 de Matemática

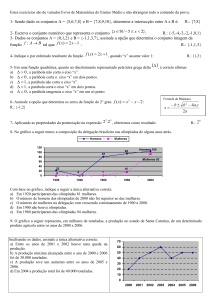
LISTA DE EXERCÍCIOS - MOODLE
Capítulo 3: Funções
1) Eventualmente, o laboratório de engenharia sanitária e ambiental da UFPa molda,
para grandes empreiteiras, alguns corpos de prova (𝑐𝑝’𝑠) – objetos cilíndricos
compostos de concreto – a fim de serem rompidos (quebrados) por meio de
ensaios de compressão axial – pressão exercida por uma força sobre um corpo,
tendendo a aproximar as partes que o compõem. O objetivo é relacionar a
resistência do corpo de prova à resistência real do concreto ao ataque de sulfatos
contidos no solo. Imagine que cada 𝑐𝑝 tenha um custo de R$ 2,00 para ser
moldado e tem uma despesa fixa semanal de R$ 50,00 com outros materiais
utilizados, como desmoldantes e fôrmas. Se forem rompidos 𝑥 𝑐𝑝’𝑠 por semana
22
ao preço de (
3
−
𝑥
30
) reais a unidade, quantos 𝑐𝑝’𝑠 devem ser rompidos por
semana para se obtiver o maior lucro possível?
Considere que Receita = Custo + Lucro.
a) 50
b) 60
c) 70
d) 80
e) 90
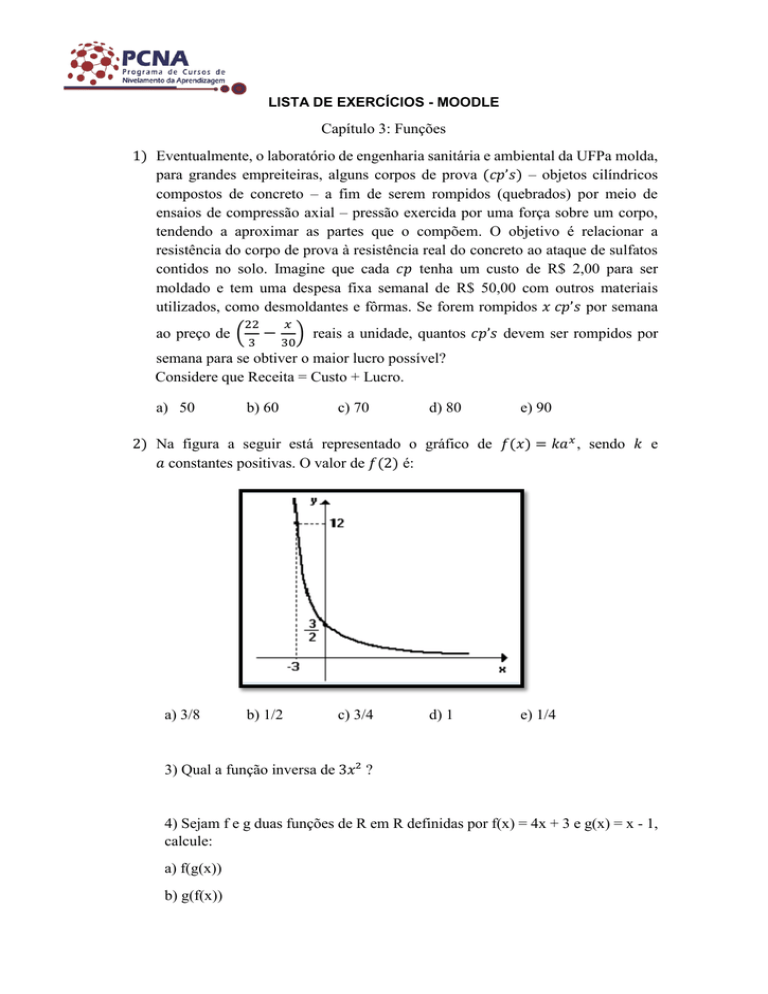
2) Na figura a seguir está representado o gráfico de 𝑓(𝑥) = 𝑘𝑎 𝑥 , sendo 𝑘 e
𝑎 constantes positivas. O valor de 𝑓(2) é:
a) 3/8
b) 1/2
c) 3/4
d) 1
e) 1/4
3) Qual a função inversa de 3𝑥² ?
4) Sejam f e g duas funções de R em R definidas por f(x) = 4x + 3 e g(x) = x - 1,
calcule:
a) f(g(x))
b) g(f(x))
c) f(g(3))
d) g(f(3))
5) Sejam f e g duas funções de R em R definidas por f(x) = 3x + k e g(x) = -2x
+ 5, sendo k uma constante real. Determine o valor de k de modo que (fog)(x) =
(gof)(x) para todo x x ϵ R.
6) A parte interior de uma taça foi gerada pela rotação de uma parábola em torno
de um eixo z, conforme mostra a figura.
A função real que expressa a parábola, no plano cartesiano da figura, é dada pela
lei 𝑓(𝑥) = 3⁄2 𝑥 2 − 6𝑥 + 𝐶, onde 𝐶 é a medida da altura do líquido contido na
taça, em centímetros. Sabe-se que o ponto V, na figura, representa o vértice da
parábola, localizado sobre o eixo x. Nessas condições, a altura do líquido contido
na taça, em centímetros, é
a) 1.
b) 2.
c) 4.
d) 5.
e) 6.
7) Construa, num eixo de sistemas ortogonais, o gráfico das seguintes funções:
a) 𝑓(𝑥) = 2𝑥 + 3
b) 𝑓(𝑥) = −2𝑥 + 5
8) Construa o gráfico da função modular 𝑓(𝑥) = 2 + |𝑥 – 1|.
9) A respeito da função real definida por 𝑓(𝑥) = 𝑙𝑜𝑔(2𝑥 − 5), faça a soma dos
números relacionados com as afirmativas corretas:
(01) 𝑓(3) = 1
(02) 𝑓(5) = 𝑙𝑜𝑔5
(04) 𝑓(7) = 0,96
(08) 𝑓(15) − 𝑓(10) = 𝑙𝑜𝑔(5⁄3)
(16) 𝐷𝑜𝑚𝑓 =]2,5 ; +∞[
Considere: 𝑙𝑜𝑔3 = 0,48
10) Faça o gráfico e determine o conjunto imagem da função.