Matemática

Estes exercícios são de variados livros de Matemática do Ensino Médio e não abrangem todo o conteúdo da prova.
1- Sendo dado os conjuntos A = {5,6,7,8} e B = {7,8,9,10}, determine a intersecção entre A e B é:
R.: {7,8}
2- Escreva o conjunto numérico que representa o conjunto {x   /  5  x  2} :
R.: {-5,-4,-3,-2,-1,0,1}
3- Dados os conjuntos A = {0,1,2} e B = {-1,1,3,7}, assinale a opção que determina o conjunto imagem da
função f : A  B tal que f ( x)  2 x  1 :
R.: {-1,1,3}
4- Indique o par ordenado resultante da função f ( x)  2 x  1 , quando “x” assume valor 1:
R.: {1,3}
5- Em uma função quadrática, quanto ao discriminante representado pela letra grega delta   , é correto afirmar:
a)   0 , a parábola não corta o eixo “x”.
b)   0 , a parábola corta o. eixo “x” em dois pontos.
c)   1 , a parábola não corta o eixo “x”.
d)   1 , a parábola corta o eixo “x” em dois pontos.
e)   0 , a parábola tangencia o eixo “x” em um só ponto.
Fórmula de Bháskara
6- Assinale a opção que determina os zeros da função do 2° grau f ( x)  x 2  x  2 :
R.: {-1,2}
x
 b  b 2  4a.c
2a
3 5
7- Aplicando as propriedades da potenciação na expressão 2 .2 , obteremos como resultado:
8
R.: 2
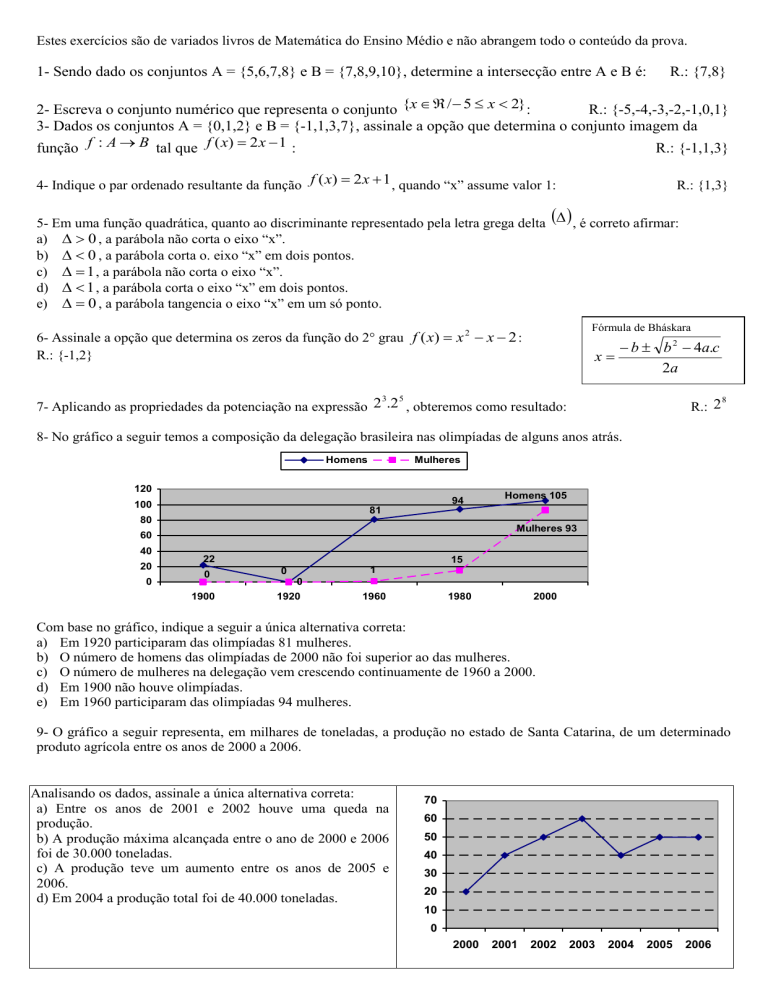
8- No gráfico a seguir temos a composição da delegação brasileira nas olimpíadas de alguns anos atrás.
Homens
Mulheres
120
94
100
80
Mulheres 93
60
40
20
0
Homens 105
81
22
0
1900
15
1
0
0
1920
1960
1980
2000
Com base no gráfico, indique a seguir a única alternativa correta:
a) Em 1920 participaram das olimpíadas 81 mulheres.
b) O número de homens das olimpíadas de 2000 não foi superior ao das mulheres.
c) O número de mulheres na delegação vem crescendo continuamente de 1960 a 2000.
d) Em 1900 não houve olimpíadas.
e) Em 1960 participaram das olimpíadas 94 mulheres.
9- O gráfico a seguir representa, em milhares de toneladas, a produção no estado de Santa Catarina, de um determinado
produto agrícola entre os anos de 2000 a 2006.
Analis Analisando os dados, assinale a única alternativa correta:
a) Entre os anos de 2001 e 2002 houve uma queda na
produção.
b) A produção máxima alcançada entre o ano de 2000 e 2006
foi de 30.000 toneladas.
c) A produção teve um aumento entre os anos de 2005 e
2006.
d) Em 2004 a produção total foi de 40.000 toneladas.
70
60
50
40
30
20
10
0
2000
2001
2002
2003
2004
2005
2006
r 27
an  a1  n  1R.:
10- Determine o sétimo termo da progressão aritmética P.A. (3, 7,11,15,...):
11- Numa progressão aritmética (P.A.) o décimo terceiro termo é 126 e o primeiro termo é igual a 6. Determine a razão
desta P.A.:
R.: 10
an  a1  n  1r
12- Numa progressão geométrica (PG) onde o sexto termo igual a 96 e a razão igual a 2, determine o primeiro termo:
R.: 3
n 1
an  a1 .q
13- Calcule o nono termo da progressão geométrica PG (21, 42, 84, ...):
R.: 5376
an  a1 .q n1
14- No primeiro dia de junho uma pessoa emprestou R$ 2.000,00 a juros simples, a uma taxa de 3,5% ao mês. Marque
abaixo o montante da dívida após 4 meses:
R.: R$ 2.280,00
j = C.i.t
15 – Antonio aplicou um capital de R$ 1.500,00, em regime de juros compostos, com uma taxa de 2% a.m. (ao mês),
durante 4 meses. Quanto representa aproximadamente o montante que será recebido após a aplicação:
R.: R$ 1.620,00
M = C(1+i)t
16 – A soma das matrizes A 
2
2
8 4
e B
3
6
4 5
é:
R.:
5
8
12 9
17 – Determine os valores corretos para os números reais x e y, de modo que as matrizes A e B sejam iguais:
A
3x  2 y
6
1
x y
e
B
9 6
R.: x = 5 e y = 3
1 2
21 – Indique o determinante correto para a matriz C 
6 7
5 8
: R.: 13
Det A 
a11
a12
a21 a22
= a11.a22 - a12 .a21
18 – Quantos números de 3 algarismos distintos podemos formar com os algarismos 1, 3 e 6:
19 – Quantas seqüências diferentes 7 livros podem ser dispostos em uma estante:
Pn = n !
20 – O número total de anagramas que podemos formar com a palavra CANTO:
R.: 6
R.: 5040
R.: 120
21 – Quantos números de 3 algarismos distintos podemos formar com os elementos do conjunto C ={0, 1, 2, 3, 6}: R.: 60
An, p
n!
(n - p) !
=
, sendo p ≤ n
22- Indique de quantos modos diferentes pode-se organizar uma comissão de três membros escolhidos entre 8
pessoas, sabendo-se que as pessoas que a formarem terão funções idênticas:
R.: 56
Cn, p
=
23- Um exemplo sobre calculo de área, mas estude a área e o volume de outras figuras:
Podemos observar a área lateral de um cilindro fazendo a sua planificação:
A área total corresponde à soma da área lateral com o dobro da área da base.
n!
, sendo p ≤ n
p!(n - p)!