Geometria Analítica

ALGA - Eng. Civil e Eng. Topográ…ca - ISE - 2010/11 - Geometria Analítica
88
Geometria Analítica
A noção de recta em R2 e R3 ; tal como a noção de plano em R3 já foram abordados no ensino
secundário. Neste capítulo faz-se um revisão desses conceitos e generaliza-se ao espaço Rn
estas noções e outras associadas.
Rectas no plano
Em geometria euclidiana existe uma única recta que passa por dois pontos dados. Para se
saber se um ponto está ou não sobre uma recta é necessário encontrar uma propriedade que
só os pontos que estão sobre a recta possuem.
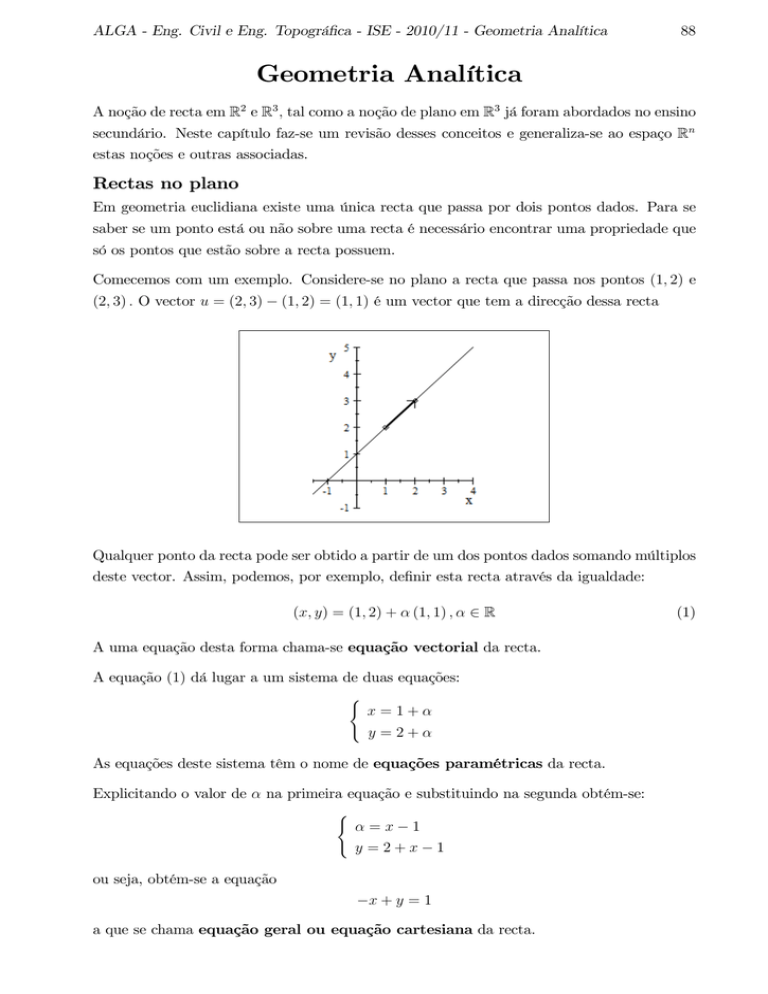
Comecemos com um exemplo. Considere-se no plano a recta que passa nos pontos (1; 2) e
(2; 3) : O vector u = (2; 3)
(1; 2) = (1; 1) é um vector que tem a direcção dessa recta
Qualquer ponto da recta pode ser obtido a partir de um dos pontos dados somando múltiplos
deste vector. Assim, podemos, por exemplo, de…nir esta recta através da igualdade:
(x; y) = (1; 2) +
(1; 1) ;
2R
A uma equação desta forma chama-se equação vectorial da recta.
A equação (1) dá lugar a um sistema de duas equações:
(
x=1+
y =2+
As equações deste sistema têm o nome de equações paramétricas da recta.
Explicitando o valor de
na primeira equação e substituindo na segunda obtém-se:
(
=x 1
y =2+x
1
ou seja, obtém-se a equação
x+y =1
a que se chama equação geral ou equação cartesiana da recta.
(1)
ALGA - Eng. Civil e Eng. Topográ…ca - ISE - 2010/11 - Geometria Analítica
89
Se nesta equação explicitarmos o valor de y obém-se:
y =x+1
a que se chama equação reduzida da recta.
Em geral, se quisermos a equação da recta que passa no ponto A = (a1 ; a2 ) e tem a direcção
do vector u = (u1 ; u2 ) temos que repetir este procedimento. Seja X = (x; y) um ponto geral
sobre a recta, então existe um número real
tal que
(x; y) = (a1 ; a2 ) + (u1 ; u2 ):
Donde passamos para as equações paramétricas:
(
x = a1 + u 1
y = a2 + u 2
Explicitando agora o valor de
e …nalmente
na primeira equação e substituindo na segunda vem
8
x a1
>
< =
u1
u2
>
: y = a2 + (x a1 )
u1
y=
u2
x + a2
u1
u2
a1
u1
A equação reduzida de uma recta é da forma y = mx + h, em que m =
u2
e h = a2
u1
u2
a1 :
u1
u2
é o valor da tangente do ângulo que a recta faz com o eixo
u1
dos xx. A este valor chama-se declive da recta.
u2
Por outro lado o valor h = a2
a1 é o que se obtém para y quando se faz x = 0: A este
u1
Como se vê facilmente m =
ALGA - Eng. Civil e Eng. Topográ…ca - ISE - 2010/11 - Geometria Analítica
90
valor chama-se ordenada na origem.
Na …gura acima estão representadas rectas de diferentes declives todas a passar na origem.
É fácil perceber que as rectas que passam na origem têm equação reduzida y = mx (com
excepção do eixo dos yy que tem equação x = 0)
Rectas paralelas
Rectas paralelas fazem todas o mesmo ângulo com o eixo dos xx, logo têm todas o mesmo
declive. As rectas da …gura têm todas declive 1 e têm ordenada na origem diferente. Pode-se
então escrever que a equação geral desta família de rectas é da forma y = x + h, variando o
h consoante o ponto onde a recta intersecta o eixo dos yy:
Exemplos
1. Determinar a equação da recta paralela à recta 2x + 3y = 6 que passa na origem.
2
Começamos por escrever a equação da recta na forma reduzida: y =
x + 2. Vemos
3
2
assim que a recta dada tem declive
: Procuramos agora entre todas as rectas com
3
ALGA - Eng. Civil e Eng. Topográ…ca - ISE - 2010/11 - Geometria Analítica
91
2
qual é a que passa no ponto (0; 0) : A equação geral das rectas paralelas
3
2
à recta dada é y =
x + h. É claro que para a recta passar na origem terá que ser
3
2
h = 0: A recta pretendida é y =
x ou seja, 2x + 3y = 0:
3
declive
2. A recta r passa nos pontos (4; 9) e ( 1; 2) : A recta s é paralela à recta r e passa no
ponto (5; 4) : Determine uma equação da recta s:
Um vector com a direcção da recta r é u = (4; 9) ( 1; 2) = (5; 11) ; daqui se conclui
11
11
que o declive da recta r é : Qualquer recta paralela a r tem declive , ou seja terá
5
5
11
equação reduzida da forma y =
x + h. Para que a recta passe no ponto (5; 4) tem
5
11
11
5 = 7: Então a equação da recta pretendida é y = x 7:
que ser h = 4
5
5
Rectas ortogonais
Considere-se a recta r = fA + u;
2 Rg e a recta s = fB + v;
A recta r tem equação reduzida y =
u2
x + a2
u1
2 Rg. Estas rectas são
ortogonais se os vectores u e v forem ortogonais. Ou seja as rectas são ortogonais se u v = 0
y=
v2
x + b2
v1
u2
a1
u1
e a recta s tem equação reduzida
v2
b1 :
v1
Como os vectores u e v são ortogonais é u v = u1 v1 + u2 v2 = 0: Desta última igualdade
u2
v1
conclui-se que
=
:
u1
v2
Então, tendo as equações reduzidas de duas rectas y = mx + h e y = m0 x + h0 , reconhece-se
1
que elas são ortogonais se m =
:
m0
Exemplos
1. Encontrar uma equação da recta perpendicular à recta 2x + 3y = 6 que passa na
origem.
ALGA - Eng. Civil e Eng. Topográ…ca - ISE - 2010/11 - Geometria Analítica
92
2
Já vimos que esta recta tem declive
: Qualquer recta perpendicular a esta terá
3
3
3
declive : Como a recta deve passar na origem a sua equação tem que ser y = x:
2
2
2. A recta r passa nos pontos (4; 9) e ( 1; 2) : A recta s é ortogonal à recta r e passa
no ponto (5; 4) : Determine uma equação da recta s:
Um vector com a direcção da recta r é u = (4; 9) ( 1; 2) = (5; 11) ; daqui se conclui
11
5
que o declive da recta r é
: Qualquer recta ortogonal a r tem declive
, ou seja
5
11
5
terá equação reduzida da forma y =
x + h. Para que a recta passe no ponto (5; 4)
11
5
69
5
69
tem que ser h = 4+
5 = : Então a equação da recta pretendida é y =
x+ :
11
11
11
11
Ângulo de duas rectas
Duas rectas concorrentes de…nem quatro ângulos, iguais dois a dois (ângulos verticalmente
opostos). A soma de dois dos ângulos diferentes é . De…ne-se ângulo de duas rectas como
o menor destes ângulos. A determinação do ângulo de duas rectas passa pelo cálculo do
ângulo entre dois vectores, um de cada recta. O ângulo obtido pode ser o maior ou o menor
dos ângulos, conforme a escolha do sentido dos vectores foi feita. Como os ângulos são
suplementares, obtido o valor de um dos ângulos facilmente se obtém o valor do outro.
Exemplos
1. Encontrar o ângulo entre as rectas de equações y =
x + 1 e 2x + 3y = 6
Temos que encontrar um vector com a direcção de cada uma das rectas. Uma maneira
fácil de o fazer é encontrar dois pontos sobre uma recta e calcular um vector de…nido
por esses dois pontos.
Para a recta y =
exemplo, u = (1; 0)
x + 1 temos, por exemplo, (0; 1) e (1; 0), donde se obtém, por
(0; 1) = (1; 1) :
Para a recta 2x + 3y = 6 temos, por exemplo, (0; 2) e (3; 0), donde se obtém, por
exemplo, v = (3; 0)
(0; 2) = (3; 2) :
ALGA - Eng. Civil e Eng. Topográ…ca - ISE - 2010/11 - Geometria Analítica
93
Temos que calcular o ângulo entre u e v para o que podemos recorrer à fórmula
u:v = kuk kvk cos ^ (u; v)
Temos então:cos ^ (u; v) =
5
(1; 1) (3; 2)
= p p donde se conclui que
k(1; 1)k k(3; 2)k
2 13
5
^ (u; v) = arccos p p ' 0:19740
2 13
Neste caso veri…ca-se facilmente, pelo sentido dos vectores escolhidos, que este é realmente o menor ângulo.
Rectas no espaço
O processo de de…nir uma recta no espaço é idêntico ao que foi usado para de…nir uma recta
no plano.
Comecemos com um exemplo. Considere-se no espaço R3 a recta que passa nos pontos
(1; 2; 3) e (2; 3; 1) : O vector u = (2; 3; 1)
(1; 2; 3) = (1; 1; 2) é um vector que tem a
direcção dessa recta. Um ponto X = (x; y; z) está sobre a recta se existir um real
tal que
(x; y; z) = (1; 2; 3) + (1; 1; 2).
8
>
< x=1+
Esta equação pode ser transformada no sistema
.
y =2+
>
:
z=3 2
8
>
< =x 1
Agindo de modo análogo ao descrito no plano temos:
y =1+x
>
:
z = 5 2x
(
(
y =1+x
z = 7 2y
Ou seja a equação cartesiana da recta é
ou
z = 5 2x
z = 5 2x
Vemos assim que para caracterizar uma recta no espaço precisamos de duas condições. Como
veremos mais à frente cada uma das condições corresponde a um plano, sendo portanto a
recta de…nida como intersecção de dois planos.
ALGA - Eng. Civil e Eng. Topográ…ca - ISE - 2010/11 - Geometria Analítica
94
Planos no espaço
Para determinar um plano em R3 são necessários três pontos não colineares, ou um ponto
e dois vectores linearmente independentes, ou um ponto e um vector ortogonal ao plano.
Repare-se que se tivermos três pontos A; B e C não colineares, podemos construir dois
vectores linearmente independentes (u = C
Ae v=B
A), assim como com um ponto
e dois vectores linearmente independentes se podem obter três pontos não colineares.
Um plano em R3 é um conjunto de pontos da forma M = fP + u + v; ;
2 Rg, em que
u e v são linearmente independentes. Um ponto do plano X = (x; y;8
z) pode assim ser obtido
> x = p1 + u1 + v 1
<
fazendo (x; y; z) = (p1 ; p2 ; p3 ) + (u1 ; u2 ; u3 ) + (v1 ; v2 ; v3 ) ou seja
y = p2 + u2 + v 2 ;
>
:
z = p3 + u3 + v 3
para algum par de valores reais para e para :
Exemplos
1. Encontrar o plano que contém os pontos A = (1; 1; 0); B = (0; 1; 1) e C = (1; 0; 1) :
De…nir dois vectores linearmente independentes:
u = B A = (0; 1; 1) (1; 1; 0) = ( 1; 0; 1);
v = C A = (1; 0; 1) (1; 1; 0) = (0; 1; 1);
O plano pretendido é o conjunto dos pontos da forma
(x; y; z) = (1; 1; 0) + ( 1; 0; 1) + (0; 1; 1)
8
>
< x=1
para algum par de valores reais e : Esta igualdade conduz ao sistema
:
y=1
>
:
z= +
Para que este sistema seja possível os valores de x; y e z têm que obedecer a uma certa
condição. É essa condição que vai conduzir à equação cartesiana do plano. Vejamos
em que condições é que este sistema, nas incógnitas
3
2
2
1
0
x 1
1 0
6
7
6
1
y 1 5 !4 0 1
4 0
1
1
z
0 0
e ; tem solução:
3
x+1
7
y + 1 5:
x+y+z 2
Para que este sistema seja possível é obrigatório que seja x+y+z 2 = 0: Esta condição
é aquela a que devem obedecer todos os pontos sobre o plano. A x + y + z
chama-se equação cartesiana do plano representado na …gura seguinte:
2=0
ALGA - Eng. Civil e Eng. Topográ…ca - ISE - 2010/11 - Geometria Analítica
95
Tem particular importância conhecer-se as intersecções dos planos com os eixos e com
os planos coordenados. Para este exemplo vê-se facilmente que as intersecções com os
eixos são (2; 0; 0) ; (0; 2; 0) e (0; 0; 2) : Quanto às intersecções com os planos coordenados
temos:
Intersecção com o plano xOy :
Intersecção com o plano xOz :
Intersecção com o plano yOz :
(
(
(
x+y+z
2=0
z=0
x+y+z
2=0
y=0
x+y+z
2=0
x=0
!
!
!
(
(
(
x+y =2
z=0
x+z =2
z=0
y+z =2
z=0
2. É também possível de…nir um plano através de um ponto por onde o plano passe e um
vector normal ao plano. Com efeito, se um vector é normal a um plano então é normal
a todos os vectores do plano. Seja P um ponto que se sabe pertencer ao plano e n um
vector ortogonal ao plano. Sendo X um ponto genérico do plano, então n é ortogonal
ao vector X
P , ou seja (X
P ) n = 0:
Vejamos como utilizar este conhecimento para de…nir o plano do exemplo anterior.
Já determinámos dois vectores do plano u = ( 1; 0; 1) e v = (0; 1; 1): Um vector
ortogonal ao plano será ortogonal a ambos os vectores simultaneamente e pode ser
facilmente obtido efectuando o produto externo de u e de v:
3
2
"
#
"
#
"
e1 e2 e3
0
1
1
1
7
6
e1 det
e2 + det
" det " 4 1
0 1 5 = det
1 1
0 1
0
1 1
1
0
0
1
#
e3 =
= e1 + e2 + e3 = (1; 1; 1) :
Assim,
(X
() (x
P ) n = 0 () ((x; y; z)
1; y
(1; 1; 0)) (1; 1; 1) = 0
1; z) (1; 1; 1) = 0 () x
1+y
1 + z = 0;
obtendo-se a equação do plano
x+y+z
2 = 0:
Ângulo de dois planos
O ângulo entre dois planos é de…nido pelo ângulo entre duas rectas que sejam, respectivamente, ortogonais a cada um dos planos.