Planif_Mat_A_11_2010_11_1P

Escola Secundária de Valongo
Disciplina: Matemática A – 11º Ano
Planificação 2010/2011
Blocos Previstos (90min) – 37
1º Período
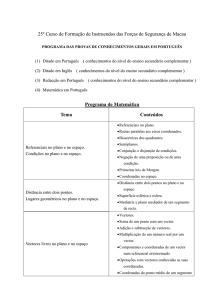
CONTEÚDOS
COMPETÊNCIAS ESPECÍFICAS
AVALIAÇÃO
GESTÃO
LECTIVA
Geometria no plano e no espaço II
Trigonometria
que • Resolver problemas ligados a situações que •
Trabalho
envolvam o cálculo de um elemento de um individualizado.
triângulo.
• Relacionar conceitos de trigonometria com • Trabalhos de
triângulos.
grupo ou de
pares.
•
Compreender
o
círculo
trigonométrico.
•
Actividades
• Ângulo e arco generalizados:
•
Localizar
um
ângulo
no
círculo
trigonométrico.
de
Avaliação
- Radiano;
Intermédia.
- Expressão geral das amplitudes dos • Reduzir um ângulo ao 1º quadrante.
•
Simplificar
expressões
trigonométricas
ângulos com os mesmos lados, em
(interpretar no círculo trigonométrico)
• Relatórios.
graus e radianos.
• Converter graus em radianos e vice-versa.
• Utilizar preferencialmente o sistema circular para
indicar a amplitude de um ângulo.
3
•
Resolução
de
problemas
envolvam triângulos.
4
1
• Funções seno, co-seno e tangente:
- Definição; variação (estudo no
círculo trigonométrico);
- Comparação de senos e co-senos de
dois números reais.
• Estudar os gráficos das funções seno, co-seno e
tangente.
• Utilizar a calculadora gráfica no estudo das
funções trigonométricas.
• Conhecer o comportamento de uma função
trigonométrica.
• Conhecer o conceito de função periódica e de
função trigonométrica como modelo matemático
adequado a responder a problemas.
•
Resolver
problemas
envolvendo
funções
trigonométricas.
• Expressão geral das amplitudes dos • Resolver equações trigonométricas elementares.
ângulos com o mesmo seno, co-seno
ou tangente.
Equações trigonométricas elementares.
7
• Composições.
•
Teste
Intermédio.
•
Testes
escritos.
• Desempenho.
• Participação.
5
• Trabalhos de
casa.
Vectores no Plano e no Espaço
• Produto escalar de dois vectores no
plano e no espaço:
- Definição e propriedades;
- Expressão do produto escalar nas
coordenadas
dos
vectores
em
referencial ortonormado.
• Calcular, num referencial ortonormado, a
amplitude do ângulo de dois vectores.
• Determinar a amplitude do ângulo de duas
rectas.
• Determinar o declive de uma recta como
tangente da inclinação no caso da equação
reduzida da recta no plano.
•
Resolver
problemas
envolvendo
perpendicularidade de vectores e de rectas
6
2
recorrendo ao produto escalar.
• Conhecer novas formas de definir conjuntos seus
conhecidos no plano, tais como: mediatriz de um
segmento de recta, circunferência ou recta
tangente a uma circunferência num ponto dado.
• Conhecer novas formas de definir conjuntos seus
conhecidos no espaço, tais como: plano mediador
e superfície esférica.
• Aplicar o conceito de produto escalar de dois
vectores
para
deduzir
a
formula
do
• Perpendicularidade de vectores e de desenvolvimento de cos( x - y).
rectas; equação cartesiana do plano
definido por um ponto e o vector • Escrever uma equação de um plano dado um
normal.
ponto e um vector normal.
• Intersecção de planos e interpretação
geométrica:
• Escrever as equações cartesianas da recta de
- Resolução de sistemas;
- Equações cartesianas da recta no intersecção de dois planos e equações de rectas a
partir de um ponto e uma direcção.
espaço.
• Determinar a intersecção de planos.
• Estabelecer as condições de paralelismo e de
• Avaliação diagnóstica, avaliação perpendicularidade no espaço.
formativa e avaliação sumativa.
• Auto-avaliação e hétero-avaliação.
6
5
1
Nota: As metodologias adoptadas para leccionar o programa da disciplina incluem: actividades de pesquisa; tarefas; fichas de trabalho;
exercícios do manual adoptado e recurso às novas tecnologias.
A elaboração destes materiais assim como as estratégias e metodologias a aplicar em cada uma das turmas neste nível de ensino serão
planeadas, em conjunto com todos os colegas a leccionar o mesmo nível, em reuniões quinzenais.
3