Enunciado e gabarito da P2 de 2014/1

Universidade Federal do Rio de Janeiro – Instituto de Fı́sica
Fı́sica III – 2014/1 – Segunda Prova: 12/05/2014
Teste
VERSÃO: A
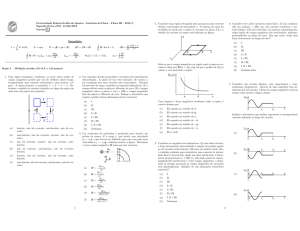
5. Por um fio retilı́neo, muito longo, em repouso, passa
uma corrente elétrica estacionária de intensidade I.
Próximo a tal fio, há um retângulo condutor, rı́gido,
coplanar com o fio, conforme mostra a figura. Originalmente, o retângulo também encontra-se em repouso, mas, em um certo instante, ele passa a se movimentar em uma das quatro maneiras seguintes: (1)
translação com velocidade ~v 1 = v1 ŷ; (2) translação
com velocidade ~v 2 = v2 x̂; (3) translação com velocidade ~v 3 = v3x x̂ + v3y ŷ, ou (4) rotação (rı́gida) em
torno do eixo do próprio fio, com velocidade angular
~ = ωẑ. Em qual(is) das quatro situações, não surge
ω
uma corrente elétrica induzida ao longo do retângulo?
3. Calcule a força magnética resultante sobre o pedaço
de fio, através do qual passa uma corrente elétrica
estacionária de intensidade I, composto por dois segmentos retilı́neos, de comprimento L, muito grande, e
uma semicircunferência de cı́rculo, de raio a, na presença de um campo magnético constante (estacionário
~ = B ŷ, B = const > 0 .
e uniforme) B
Formulário
~ m = q~v × B
~ ,
F
I
~ m = Id~ℓ × B
~ ,
dF
~ ·dA
~ = 0,
B
~ =
dB
S
I
Seção 1.
~ d~ℓ = µ0 Ienc + µ0 ǫ0 dΦE ,
B·
dt
C
Eind = −
dΦB
,
dt
ΦB = LI ,
µ0 Id~ℓ × r̂
,
4π
r2
uB =
1 B2
.
2 µ0
Múltipla escolha (8×0,6 = 4,8 pontos)
1. Uma barra de comprimento a ocupa uma região onde
há um campo magnético constante (estacionário e uni~ A barra gira com velocidade angular ω
~,
forme) B.
em torno de um ponto fixo em uma de suas extremidades, em um plano perpendicular ao campo. Qual
é o módulo da tensão ou da diferença de potencial
que acaba se estabelecendo entre as extremidades da
barra?
(a)
ωa2 B/4 .
(b)
2ωa2 B .
(c)
ωa2 B .
(d)
ωa2 B/2 .
(e)
2πωa2 B .
(f)
πωa2 B .
(g)
0.
2. Calcule o campo magnético no ponto P devido ao circuito com corrente estacionária de intensidade I.
µ0 I 1 1
(a) −
ẑ .
−
4
a b
µ0 I 1 1
−
ẑ .
(b)
4
a b
µ0 I 1 1
(c) −
−
ẑ .
2
a b
µ0 I 1 1
(d)
ẑ .
−
2
a b
µ0 I 1 1
ẑ .
−
(e) −
2π a b
µ0 I 1 1
(f)
−
ẑ .
2π a b
µ0 I 1 1
−
ẑ .
(g) −
4π a b
µ0 I 1 1
(h)
−
ẑ .
4π a b
1
(a)
2IaB ẑ .
(b)
−2IaB ẑ .
(c)
2ILB ẑ .
(d)
−2ILB ẑ .
(e)
2I(a + L)B ẑ .
(f)
−2I(a + L)B ẑ .
(g)
2I(a − L)B ẑ .
(h)
−2I(a − L)B ẑ .
4. Todas as partı́culas carregadas que passam através
de uma região em que existem campos elétrico e
magnético constantes, ortogonais, sem serem defletidas têm em comum
(a)
a massa.
(b)
o momento linear.
(c)
a velocidade.
(d)
a energia.
(e)
a razão entre carga e massa.
2
(a)
Somente em 1.
(b)
Somente em 4.
(c)
Somente em 2.
(d)
Somente em 3.
(e)
Em 1 e 4.
(f)
Em 2 e 3.
(g)
Em nenhuma surgirá corrente induzida, pois o
campo gerado pelo fio, mantém-se estacionário
e a ŕea do retângulo não varia.
7. Seja um solenóide longo, formado por um enrolamento
de espiras circulares. Considere as seguintes três afirmativas sobre sua auto-indutância: (I) ela é proporcional ao quadrado do raio das espiras; (II) ela é proporcional à taxa de variação da corrente no solenóide,
e (III) ela é proporcional à corrente que circula no solenóide. Assinale a opção que indica qual(is) dessas
afirmativas está(ão) correta(s).
6. Um capacitor de placas paralelas, circulares e cujo
raio das placas é muito maior que a distância entre as
mesmas está inicialmente descarregado. A partir de
um certo instante, o capacitor começa a ser carregado
por uma corrente que cresce linearmente com o tempo
i(t) = bt, onde b = const > 0. Sobre os campos
elétrico e magnético que podem eventualmente surgir
entre as placas durante o carregamento do capacitor
pode-se afirmar que:
(a)
Nenhuma das afirmativas está correta.
(a)
surgirá apenas um campo elétrico estacionário.
(b)
Apenas a I.
(b)
surgirão um campo elétrico estacionário e um
campo magnético não estacionário, colineares
entre si.
(c)
Apenas a II.
(d)
Apenas a III.
Apenas a I e a II.
(c)
surgirá apenas um campo elétrico não estacionário.
(e)
(f)
Apenas a I e a III.
(d)
surgirão um campo elétrico não estacionário e
um campo magnético estacionário, colineares
entre si.
(g)
Apenas a II e a III.
(h)
Todas as afirmativas estão corretas.
(e)
(f)
8. Considere as seguintes três afirmações sobre a lei de
Ampère: (I) ela só vale quando há um alto grau de
simetria da distribuição de correntes; (II) ela só vale
quando as correntes forem estacionárias, e (III) ela
só vale quando os campos magnéticos forem estacionários. Assinale a alternativa que indica qual(is)
de tais afirmações é(são) correta(s).
surgirão um campo elétrico não estacionário e
um campo magnético estacionário, perpendiculares entre si.
surgirão um campo elétrico e um campo
magnético, ambos não estacionários, e perpendiculares entre si.
(a)
Nenhuma afirmação é correta.
(b)
Somente a I.
(c)
Somente a II.
(d)
Somente a III.
(e)
Somente a I e a II.
(f)
Somente a I e a III.
(g)
Somente a II e a III.
(h)
Todas as afirmações são corretas.
(a) Qual é a (intensidade de) corrente elétrica no fio interno? [0,6 ponto]
(b) Qual é a (intensidade de) corrente elétrica na casca externa? [0,4 ponto]
~ em cada uma das quatro regiões em que o cabo “divide” o espaço. [1,6 ponto]
(c) Determine o campo magnético B
2. [2,6 pontos] Um pedaço de fio condutor ôhmico isolado é torcido de modo a constituir um circuito em forma de
oito. Por razão de simplicidade, modele as duas metades da figura de oito como circunferências de cı́rculo. O
raio do cı́rculo superior é a e o do inferior é 2a. O circuito completo é puramente resistivo (com capacitância e
auto-indutância desprezı́veis), tendo resistência R. A partir de t = 0 s, um campo magnético uniforme, mas não
estacionário,
~ = Ct ẑ ,
B
onde C = const > 0, é aplicado perpendicularmente ao plano dos dois cı́rculos, conforme mostrado na figura.
Seção 2. Questões discursivas (2×2,6 = 5,2 pontos)
Todas as respostas devem ter justificativas!
1. [2,6 pontos] Um cabo coaxial é composto por um fio sólido, cilı́ndrico, circular, de raio R, envolto por uma casca
espessa, cilı́ndrica, também circular, coaxial, de raios a e b, tais que R < a < b. Ambos os cilindros são muito
longos e têm o eixo comum Z. Através do fio interno, passa uma corrente elétrica estacionária, cuja densidade de
~ int = Cr ẑ, onde C = const > 0 e r é a distância até o eixo do fio. Através da casca externa,
corrente é dada por J
~ ext = −J0 ẑ, onde J0 = const > 0.
passa uma corrente estacionária, cuja densidade de corrente é dada por J
3
(a) Para t > 0 s, determine o fluxo total através do circuito. [1,2 ponto]
(b) Para t > 0 s, determine o sentido da corrente elétrica induzida ao longo do fio, indicando-o claramente em
cada uma das circunferências, seja por intermédio de uma seta, seja pelas expressões horário ou anti-horário.
[0,6 ponto]
(c) Para t > 0 s, determine o módulo da intensidade da corrente elétrica induzida no fio. [0,8 ponto]
4
Gabarito para Versão A
Seção 1.
Múltipla escolha (8×0,6 = 4,8 pontos)
1. Uma barra de comprimento a ocupa uma região onde
há um campo magnético constante (estacionário e uni~ A barra gira com velocidade angular ω
~,
forme) B.
em torno de um ponto fixo em uma de suas extremidades, em um plano perpendicular ao campo. Qual
é o módulo da tensão ou da diferença de potencial
que acaba se estabelecendo entre as extremidades da
barra?
3. Calcule a força magnética resultante sobre o pedaço
de fio, através do qual passa uma corrente elétrica
estacionária de intensidade I, composto por dois segmentos retilı́neos, de comprimento L, muito grande, e
uma semicircunferência de cı́rculo, de raio a, na presença de um campo magnético constante (estacionário
~ = B ŷ, B = const > 0 .
e uniforme) B
5. Por um fio retilı́neo, muito longo, em repouso, passa
uma corrente elétrica estacionária de intensidade I.
Próximo a tal fio, há um retângulo condutor, rı́gido,
coplanar com o fio, conforme mostra a figura. Originalmente, o retângulo também encontra-se em repouso, mas, em um certo instante, ele passa a se movimentar em uma das quatro maneiras seguintes: (1)
translação com velocidade ~v 1 = v1 ŷ; (2) translação
com velocidade ~v 2 = v2 x̂; (3) translação com velocidade ~v 3 = v3x x̂ + v3y ŷ, ou (4) rotação (rı́gida) em
torno do eixo do próprio fio, com velocidade angular
~ = ωẑ. Em qual(is) das quatro situações, não surge
ω
uma corrente elétrica induzida ao longo do retângulo?
7. Seja um solenóide longo, formado por um enrolamento
de espiras circulares. Considere as seguintes três afirmativas sobre sua auto-indutância: (I) ela é proporcional ao quadrado do raio das espiras; (II) ela é proporcional à taxa de variação da corrente no solenóide,
e (III) ela é proporcional à corrente que circula no solenóide. Assinale a opção que indica qual(is) dessas
afirmativas está(ão) correta(s).
(a)
Nenhuma das afirmativas está correta.
(b)
Apenas a I.
(c)
Apenas a II.
(d)
Apenas a III.
(a)
ωa2 B/4 .
(e)
Apenas a I e a II.
(b)
2ωa2 B .
(f)
Apenas a I e a III.
(c)
ωa2 B .
(g)
Apenas a II e a III.
(d)
ωa2 B/2 .
(h)
Todas as afirmativas estão corretas.
(e)
2πωa2 B .
(f)
πωa2 B .
(g)
0.
2. Calcule o campo magnético no ponto P devido ao circuito com corrente estacionária de intensidade I.
µ0 I 1 1
(a) −
−
ẑ .
4
a b
µ0 I 1 1
ẑ .
−
(b)
4
a b
µ0 I 1 1
(c) −
−
ẑ .
2
a b
µ0 I 1 1
−
ẑ .
(d)
2
a b
µ0 I 1 1
(e) −
−
ẑ .
2π a b
µ0 I 1 1
(f)
−
ẑ .
2π a b
µ0 I 1 1
−
(g) −
ẑ .
4π a b
µ0 I 1 1
(h)
−
ẑ .
4π a b
(a)
2IaB ẑ .
(b)
−2IaB ẑ .
(c)
2ILB ẑ .
(d)
−2ILB ẑ .
(a)
Somente em 1.
(e)
2I(a + L)B ẑ .
(b)
Somente em 4.
(f)
−2I(a + L)B ẑ .
(c)
Somente em 2.
(g)
2I(a − L)B ẑ .
(d)
Somente em 3.
(h)
−2I(a − L)B ẑ .
(e)
Em 1 e 4.
(f)
Em 2 e 3.
(g)
4. Todas as partı́culas carregadas que passam através
de uma região em que existem campos elétrico e
magnético constantes, ortogonais, sem serem defletidas têm em comum
1
Em nenhuma surgirá corrente induzida, pois o
campo gerado pelo fio, mantém-se estacionário
e a ŕea do retângulo não varia.
6. Um capacitor de placas paralelas, circulares e cujo
raio das placas é muito maior que a distância entre as
mesmas está inicialmente descarregado. A partir de
um certo instante, o capacitor começa a ser carregado
por uma corrente que cresce linearmente com o tempo
i(t) = bt, onde b = const > 0. Sobre os campos
elétrico e magnético que podem eventualmente surgir
entre as placas durante o carregamento do capacitor
pode-se afirmar que:
(a)
a massa.
(b)
o momento linear.
(a)
surgirá apenas um campo elétrico estacionário.
(c)
a velocidade.
(b)
(d)
a energia.
(e)
a razão entre carga e massa.
surgirão um campo elétrico estacionário e um
campo magnético não estacionário, colineares
entre si.
(c)
surgirá apenas um campo elétrico não estacionário.
2
8. Considere as seguintes três afirmações sobre a lei de
Ampère: (I) ela só vale quando há um alto grau de
simetria da distribuição de correntes; (II) ela só vale
quando as correntes forem estacionárias, e (III) ela
só vale quando os campos magnéticos forem estacionários. Assinale a alternativa que indica qual(is)
de tais afirmações é(são) correta(s).
(a)
Nenhuma afirmação é correta.
(b)
Somente a I.
(c)
Somente a II.
(d)
Somente a III.
(e)
Somente a I e a II.
(f)
Somente a I e a III.
(g)
Somente a II e a III.
(h)
Todas as afirmações são corretas.
ou seja,
Seção 2. Questões discursivas (2×2,6 = 5,2 pontos)
2
Iint = πCR3 .
3
Todas as respostas devem ter justificativas!
1. [2,6 pontos] Um cabo coaxial é composto por um fio sólido, cilı́ndrico, circular, de raio R, envolto por uma casca
espessa, cilı́ndrica, também circular, coaxial, de raios a e b, tais que R < a < b. Ambos os cilindros são muito
longos e têm o eixo comum Z. Através do fio interno, passa uma corrente elétrica estacionária, cuja densidade de
~ int = Cr ẑ, onde C = const > 0 e r é a distância até o eixo do fio. Através da casca externa,
corrente é dada por J
~ ext = −J0 ẑ, onde J0 = const > 0.
passa uma corrente estacionária, cuja densidade de corrente é dada por J
(1)
(b) [0,4] Na casca externa, temos
Iext =
Z
Jext · n̂ dA
ZSext
(−J0 ẑ) · ẑ dA
Z
= −J0
dA
=
Sext
Sext
= −J0 Aext ,
ou seja,
Iext = −J0 π(b2 − a2 ) .
(2)
(c) [1,6] Devido à simetria cilı́ndrica da distribuição estacionária de corrente e à lei de Gauss do magnetismo, em
qualquer uma das quatro regiões, o campo magnético, só terá componente azimutal (circular), ou seja,1
~
B(r,
ϕ) = Bϕ (r) ϕ̂(ϕ) .
Isso tudo sugere, pois, que usemos a lei de Ampère e que tomemos, como curva ampèriana, uma circunferência de
cı́rculo, concêntrico com o eixo da distribuição de corrente e perpendicular ao seu eixo, de raio genérico r. Assim,
a expressão funcional para a circulação do campo magnético ao longo da ampériana fica, em qualquer uma das
quatro regiões, igual a
I
~ · dℓ
ΓB
[C]
:=
B
~
IC
Bϕ (r) ϕ̂(ϕ) · dℓϕ ϕ̂
=
IC
Bϕ (r)dℓϕ
=
C
I
= Bϕ (r) dℓϕ ,
(a) Qual é a (intensidade de) corrente elétrica no fio interno? [0,6 ponto]
(b) Qual é a (intensidade de) corrente elétrica na casca externa? [0,4 ponto]
~ em cada uma das quatro regiões em que o cabo “divide” o espaço. [1,6 ponto]
(c) Determine o campo magnético B
Resolução:
C
(a) [0,6] A intensidade de corrrente elétrica I[S] através de uma superfı́cie S e a densidade de corrente elétrica
~ , estão relacionadas por
nela, J
Z
~ · n̂ dA .
J
I[S] =
ou seja,
ΓB
~ [C] = 2πrBϕ (r) .
A intensidade de corrente encerrada pela curva ampèriana dependerá, contudo, da região em questão. De fato,
S
Logo, para uma seção reta do fio interno, temos
Iint =
=
Z
ZSint
• 0 ≤ r ≤ R: nesse caso, a corrente encerrada Ienc (r) é dada pela Eq. (1), contanto que, nela, troquemos R por
r, ou seja:
Crẑ · ẑ dA
Ienc (r) = Iint (r)
2
= πCr 3 .
3
Cr 2πr dr
Sint
= 2πC
3
Z
R
r 2 dr ,
r=0
1
A rigor, ainda poderia haver uma componente axial constante, que, suporemos nula, como usual.
4
Então, pela lei de Ampère, vem
2. [2,6 pontos] Um pedaço de fio condutor ôhmico isolado é torcido de modo a constituir um circuito em forma de
oito. Por razão de simplicidade, modele as duas metades da figura de oito como circunferências de cı́rculo. O
raio do cı́rculo superior é a e o do inferior é 2a. O circuito completo é puramente resistivo (com capacitância e
auto-indutância desprezı́veis), tendo resistência R. A partir de t = 0 s, um campo magnético uniforme, mas não
estacionário,
~ = Ct ẑ ,
B
2
Bϕ (r)2πr = µ0 πCr 3 ,
3
e, finalmente,
~ = 1 µ0 Cr 2 ϕ̂ .
B
3
onde C = const > 0, é aplicado perpendicularmente ao plano dos dois cı́rculos, conforme mostrado na figura.
• R ≤ r ≤ a: nesse caso, a corrente encerrada Ienc (r) é dada pela corrente toda do fio interno, ou seja, pela
Eq. (1):
Ienc (r) = Iint
2
= πCR3 .
3
Então, pela lei de Ampère, vem
2
Bϕ (r)2πr = µ0 πCR3 ,
3
e, finalmente,
3
~ = µ0 Iint ϕ̂ = 1 µ0 CR ϕ̂ .
B
2πr
3 r
• a ≤ r ≤ b: nesse caso, a corrente encerrada Ienc (r) é dada pela corrente do fio interno mais a corrente na casca
externa, Eq, (2), contanto que, nessa última, troquemos b por r, ou seja:
Ienc (r) = Iint + Iext (r)
2
= πCR3 − J0 π(r 2 − a2 ) .
3
Resolução:
Então, pela lei de Ampère, vem
Bϕ (r)2πr = µ0 π
(a) Para t > 0 s, determine o fluxo total através do circuito. [1,2 ponto]
(b) Para t > 0 s, determine o sentido da corrente elétrica induzida ao longo do fio, indicando-o claramente em
cada uma das circunferências, seja por intermédio de uma seta, seja pelas expressões horário ou anti-horário.
[0,6 ponto]
(c) Para t > 0 s, determine o módulo da intensidade da corrente elétrica induzida no fio. [0,8 ponto]
2
πCR3 − J0 (r 2 − a2 ) ,
3
(a) [1,2] Tomaremos como orientação positiva da curva C que modela o circuito aquela indicada na figura, de modo
que os versores nas suas partes inferior e superior são dados por
e, finalmente,
a2
1 CR3 1
~
ϕ̂ .
− J0 r −
B = µ0
3 r
2
r
• b ≤ r < ∞: nesse caso, a corrente encerrada Ienc (r) é dada pela corrente total, Eq. (1) + Eq. (2), do fio interno
mais a corrente na casca externa, ou seja:
Ienc (r) = Iint + Iext .
Então, pela lei de Ampère, vem
Bϕ (r)2πr = µ0 (Iint + Iext ) ,
e, finalmente,
~ = µ0 Iint + Iext ϕ̂ .
B
2πr
n̂sup = −ẑ
n̂inf = ẑ .
5
6
Então, o fluxo através do cı́rculo superior é
Φsup :=
(c) [0,8] Pela lei de Faraday, temos que a força eletromotriz (fem) induzida ao longo do circuito é, tendo em vista
a Eq. (3),
Z
~ · n̂ dA
B
dΦ
dt
= −3πCa2 .
Ssup
=
Z
Eind [C] = −
(Ctẑ) · n̂sup dA
Ssup
Z
(Ctẑ) · (−ẑ) dA
Z
dA
= −Ct
Como o circuito é puramente resistivo e satisfaz a lei de Ohm, temos que a corrente elétrica induzida vale
= −CtAsup
= −πCta2 .
ou seja,
=
Ssup
Iind =
;S sup
|Iind | =
Analgoamente, para o fluxo através do cı́rculo inferior, temos
Φinf = CtAinf
= 4πCta2 .
Logo, o fluxo total através do circuito é
Φ = Φsup + Φinf
ou seja,
Φ = 3πCa2 t .
(3)
(b) [0,6 ponto] Como, nitidamente, o módulo do fluxo está aumentando e a maior contribuição para ele vem do
cı́rculo inferior, deverá surgir, pela lei de Lenz, uma corrente induzida que parcialmente cancelará, por intermédio
do correspondente campo magnético “induzido”, no centro do cı́rculo inferior, o campo magnético externo. Isso
implica que a corrente induzida terá o sentido indicado pelas setas na figura a seguir, ou ainda,
• circunferência inferior: sentido horário
• circunferência superior: sentido anti-horário .
7
8
Eind
,
R
3πCa2
.
R
Universidade Federal do Rio de Janeiro – Instituto de Fı́sica
Fı́sica III – 2014/1 – Segunda Prova: 12/05/2014
Teste
VERSÃO: B
Formulário
~ m = q~v × B
~ ,
F
I
~ m = Id~ℓ × B
~ ,
dF
~ ·dA
~ = 0,
B
~ =
dB
S
I
Seção 1.
~ d~ℓ = µ0 Ienc + µ0 ǫ0 dΦE ,
B·
dt
C
Eind = −
dΦB
,
dt
ΦB = LI ,
µ0 Id~ℓ × r̂
,
4π
r2
uB =
1 B2
.
2 µ0
5. Todas as partı́culas carregadas que passam através
de uma região em que existem campos elétrico e
magnético constantes, ortogonais, sem serem defletidas têm em comum
3. Calcule o campo magnético no ponto P devido ao circuito com corrente estacionária de intensidade I.
µ0 I 1 1
(a) −
−
ẑ .
4
a b
µ0 I 1 1
(b)
−
ẑ .
4
a b
µ0 I 1 1
ẑ .
−
(c) −
2
a b
µ0 I 1 1
(d)
ẑ .
−
2
a b
µ0 I 1 1
(e) −
−
ẑ .
2π a b
µ0 I 1 1
−
ẑ .
(f)
2π a b
µ0 I 1 1
(g) −
−
ẑ .
4π a b
µ0 I 1 1
−
ẑ .
(h)
4π a b
(a)
a massa.
(b)
o momento linear.
(c)
a velocidade.
(d)
a energia.
(e)
a razão entre carga e massa.
Múltipla escolha (8×0,6 = 4,8 pontos)
1. Uma barra de comprimento a ocupa uma região onde
há um campo magnético constante (estacionário e uni~ A barra gira com velocidade angular ω
~,
forme) B.
em torno de um ponto fixo em uma de suas extremidades, em um plano perpendicular ao campo. Qual
é o módulo da tensão ou da diferença de potencial
que acaba se estabelecendo entre as extremidades da
barra?
2. Um capacitor de placas paralelas, circulares e cujo
raio das placas é muito maior que a distância entre as
mesmas está inicialmente descarregado. A partir de
um certo instante, o capacitor começa a ser carregado
por uma corrente que cresce linearmente com o tempo
i(t) = bt, onde b = const > 0. Sobre os campos
elétrico e magnético que podem eventualmente surgir
entre as placas durante o carregamento do capacitor
pode-se afirmar que:
(a)
ωa2 B/4 .
(b)
2ωa2 B .
(a)
surgirá apenas um campo elétrico estacionário.
(c)
ωa2 B .
(b)
(d)
ωa2 B/2 .
surgirão um campo elétrico estacionário e um
campo magnético não estacionário, colineares
entre si.
(e)
2πωa2 B .
(c)
(f)
πωa2 B .
surgirá apenas um campo elétrico não estacionário.
(g)
0.
(d)
surgirão um campo elétrico não estacionário e
um campo magnético estacionário, colineares
entre si.
(e)
(f)
1
4. Calcule a força magnética resultante sobre o pedaço
de fio, através do qual passa uma corrente elétrica
estacionária de intensidade I, composto por dois segmentos retilı́neos, de comprimento L, muito grande, e
uma semicircunferência de cı́rculo, de raio a, na presença de um campo magnético constante (estacionário
~ = B ŷ, B = const > 0 .
e uniforme) B
6. Seja um solenóide longo, formado por um enrolamento
de espiras circulares. Considere as seguintes três afirmativas sobre sua auto-indutância: (I) ela é proporcional ao quadrado do raio das espiras; (II) ela é proporcional à taxa de variação da corrente no solenóide,
e (III) ela é proporcional à corrente que circula no solenóide. Assinale a opção que indica qual(is) dessas
afirmativas está(ão) correta(s).
(a)
2IaB ẑ .
(a)
Nenhuma das afirmativas está correta.
(b)
−2IaB ẑ .
(b)
Apenas a I.
Apenas a II.
(c)
2ILB ẑ .
(c)
surgirão um campo elétrico não estacionário e
um campo magnético estacionário, perpendiculares entre si.
(d)
−2ILB ẑ .
(d)
Apenas a III.
(e)
2I(a + L)B ẑ .
(e)
Apenas a I e a II.
surgirão um campo elétrico e um campo
magnético, ambos não estacionários, e perpendiculares entre si.
(f)
−2I(a + L)B ẑ .
(f)
Apenas a I e a III.
(g)
2I(a − L)B ẑ .
(g)
Apenas a II e a III.
(h)
−2I(a − L)B ẑ .
(h)
Todas as afirmativas estão corretas.
2
7. Por um fio retilı́neo, muito longo, em repouso, passa
uma corrente elétrica estacionária de intensidade I.
Próximo a tal fio, há um retângulo condutor, rı́gido,
coplanar com o fio, conforme mostra a figura. Originalmente, o retângulo também encontra-se em repouso, mas, em um certo instante, ele passa a se movimentar em uma das quatro maneiras seguintes: (1)
translação com velocidade ~v 1 = v1 ŷ; (2) translação
com velocidade ~v 2 = v2 x̂; (3) translação com velocidade ~v 3 = v3x x̂ + v3y ŷ, ou (4) rotação (rı́gida) em
torno do eixo do próprio fio, com velocidade angular
~ = ωẑ. Em qual(is) das quatro situações, não surge
ω
uma corrente elétrica induzida ao longo do retângulo?
8. Considere as seguintes três afirmações sobre a lei de
Ampère: (I) ela só vale quando há um alto grau de
simetria da distribuição de correntes; (II) ela só vale
quando as correntes forem estacionárias, e (III) ela
só vale quando os campos magnéticos forem estacionários. Assinale a alternativa que indica qual(is)
de tais afirmações é(são) correta(s).
(a)
Nenhuma afirmação é correta.
(b)
Somente a I.
(c)
Somente a II.
(d)
Somente a III.
(e)
Somente a I e a II.
(f)
Somente a I e a III.
(g)
Somente a II e a III.
(h)
Todas as afirmações são corretas.
(a) Qual é a (intensidade de) corrente elétrica no fio interno? [0,6 ponto]
(b) Qual é a (intensidade de) corrente elétrica na casca externa? [0,4 ponto]
~ em cada uma das quatro regiões em que o cabo “divide” o espaço. [1,6 ponto]
(c) Determine o campo magnético B
(a)
Somente em 1.
(b)
Somente em 4.
(c)
Somente em 2.
(d)
Somente em 3.
(e)
Em 1 e 4.
(f)
Em 2 e 3.
(g)
Em nenhuma surgirá corrente induzida, pois o
campo gerado pelo fio, mantém-se estacionário
e a ŕea do retângulo não varia.
2. [2,6 pontos] Um pedaço de fio condutor ôhmico isolado é torcido de modo a constituir um circuito em forma de
oito. Por razão de simplicidade, modele as duas metades da figura de oito como circunferências de cı́rculo. O
raio do cı́rculo superior é a e o do inferior é 2a. O circuito completo é puramente resistivo (com capacitância e
auto-indutância desprezı́veis), tendo resistência R. A partir de t = 0 s, um campo magnético uniforme, mas não
estacionário,
~ = Ct ẑ ,
B
onde C = const > 0, é aplicado perpendicularmente ao plano dos dois cı́rculos, conforme mostrado na figura.
Seção 2. Questões discursivas (2×2,6 = 5,2 pontos)
Todas as respostas devem ter justificativas!
1. [2,6 pontos] Um cabo coaxial é composto por um fio sólido, cilı́ndrico, circular, de raio R, envolto por uma casca
espessa, cilı́ndrica, também circular, coaxial, de raios a e b, tais que R < a < b. Ambos os cilindros são muito
longos e têm o eixo comum Z. Através do fio interno, passa uma corrente elétrica estacionária, cuja densidade de
~ int = Cr ẑ, onde C = const > 0 e r é a distância até o eixo do fio. Através da casca externa,
corrente é dada por J
~ ext = −J0 ẑ, onde J0 = const > 0.
passa uma corrente estacionária, cuja densidade de corrente é dada por J
3
(a) Para t > 0 s, determine o fluxo total através do circuito. [1,2 ponto]
(b) Para t > 0 s, determine o sentido da corrente elétrica induzida ao longo do fio, indicando-o claramente em
cada uma das circunferências, seja por intermédio de uma seta, seja pelas expressões horário ou anti-horário.
[0,6 ponto]
(c) Para t > 0 s, determine o módulo da intensidade da corrente elétrica induzida no fio. [0,8 ponto]
4
Gabarito para Versão B
Seção 1.
Múltipla escolha (8×0,6 = 4,8 pontos)
3. Calcule o campo magnético no ponto P devido ao circuito com corrente estacionária de intensidade I.
µ0 I 1 1
(a) −
−
ẑ .
4
a b
µ0 I 1 1
(b)
−
ẑ .
4
a b
µ0 I 1 1
−
ẑ .
(c) −
2
a b
µ0 I 1 1
(d)
−
ẑ .
2
a b
µ0 I 1 1
−
ẑ .
(e) −
2π a b
µ0 I 1 1
(f)
−
ẑ .
2π a b
µ0 I 1 1
ẑ .
−
(g) −
4π a b
µ0 I 1 1
(h)
ẑ .
−
4π a b
1. Uma barra de comprimento a ocupa uma região onde
há um campo magnético constante (estacionário e uni~ A barra gira com velocidade angular ω
~,
forme) B.
em torno de um ponto fixo em uma de suas extremidades, em um plano perpendicular ao campo. Qual
é o módulo da tensão ou da diferença de potencial
que acaba se estabelecendo entre as extremidades da
barra?
(a)
ωa2 B/4 .
(b)
2ωa2 B .
(c)
ωa2 B .
(d)
ωa2 B/2 .
(e)
2πωa2 B .
(f)
πωa2 B .
(g)
0.
2. Um capacitor de placas paralelas, circulares e cujo
raio das placas é muito maior que a distância entre as
mesmas está inicialmente descarregado. A partir de
um certo instante, o capacitor começa a ser carregado
por uma corrente que cresce linearmente com o tempo
i(t) = bt, onde b = const > 0. Sobre os campos
elétrico e magnético que podem eventualmente surgir
entre as placas durante o carregamento do capacitor
pode-se afirmar que:
(a)
surgirá apenas um campo elétrico estacionário.
(b)
surgirão um campo elétrico estacionário e um
campo magnético não estacionário, colineares
entre si.
(c)
surgirá apenas um campo elétrico não estacionário.
(d)
surgirão um campo elétrico não estacionário e
um campo magnético estacionário, colineares
entre si.
(e)
surgirão um campo elétrico não estacionário e
um campo magnético estacionário, perpendiculares entre si.
surgirão um campo elétrico e um campo
magnético, ambos não estacionários, e perpendiculares entre si.
(f)
6. Seja um solenóide longo, formado por um enrolamento
de espiras circulares. Considere as seguintes três afirmativas sobre sua auto-indutância: (I) ela é proporcional ao quadrado do raio das espiras; (II) ela é proporcional à taxa de variação da corrente no solenóide,
e (III) ela é proporcional à corrente que circula no solenóide. Assinale a opção que indica qual(is) dessas
afirmativas está(ão) correta(s).
4. Calcule a força magnética resultante sobre o pedaço
de fio, através do qual passa uma corrente elétrica
estacionária de intensidade I, composto por dois segmentos retilı́neos, de comprimento L, muito grande, e
uma semicircunferência de cı́rculo, de raio a, na presença de um campo magnético constante (estacionário
~ = B ŷ, B = const > 0 .
e uniforme) B
(a)
2IaB ẑ .
(b)
−2IaB ẑ .
(c)
2ILB ẑ .
(d)
−2ILB ẑ .
(e)
2I(a + L)B ẑ .
(f)
−2I(a + L)B ẑ .
(g)
2I(a − L)B ẑ .
(h)
−2I(a − L)B ẑ .
5. Todas as partı́culas carregadas que passam através
de uma região em que existem campos elétrico e
magnético constantes, ortogonais, sem serem defletidas têm em comum
1
(a)
a massa.
(b)
o momento linear.
(c)
a velocidade.
(d)
a energia.
(e)
a razão entre carga e massa.
2
(a)
Nenhuma das afirmativas está correta.
(b)
Apenas a I.
(c)
Apenas a II.
(d)
Apenas a III.
(e)
Apenas a I e a II.
(f)
Apenas a I e a III.
(g)
Apenas a II e a III.
(h)
Todas as afirmativas estão corretas.
7. Por um fio retilı́neo, muito longo, em repouso, passa
uma corrente elétrica estacionária de intensidade I.
Próximo a tal fio, há um retângulo condutor, rı́gido,
coplanar com o fio, conforme mostra a figura. Originalmente, o retângulo também encontra-se em repouso, mas, em um certo instante, ele passa a se movimentar em uma das quatro maneiras seguintes: (1)
translação com velocidade ~v 1 = v1 ŷ; (2) translação
com velocidade ~v 2 = v2 x̂; (3) translação com velocidade ~v 3 = v3x x̂ + v3y ŷ, ou (4) rotação (rı́gida) em
torno do eixo do próprio fio, com velocidade angular
~ = ωẑ. Em qual(is) das quatro situações, não surge
ω
uma corrente elétrica induzida ao longo do retângulo?
8. Considere as seguintes três afirmações sobre a lei de
Ampère: (I) ela só vale quando há um alto grau de
simetria da distribuição de correntes; (II) ela só vale
quando as correntes forem estacionárias, e (III) ela
só vale quando os campos magnéticos forem estacionários. Assinale a alternativa que indica qual(is)
de tais afirmações é(são) correta(s).
(a)
Nenhuma afirmação é correta.
(b)
Somente a I.
(c)
Somente a II.
(d)
Somente a III.
(e)
Somente a I e a II.
(f)
Somente a I e a III.
(g)
Somente a II e a III.
(h)
Todas as afirmações são corretas.
(a) Qual é a (intensidade de) corrente elétrica no fio interno? [0,6 ponto]
(b) Qual é a (intensidade de) corrente elétrica na casca externa? [0,4 ponto]
~ em cada uma das quatro regiões em que o cabo “divide” o espaço. [1,6 ponto]
(c) Determine o campo magnético B
(a)
Somente em 1.
(b)
Somente em 4.
(c)
Somente em 2.
Resolução:
(d)
Somente em 3.
(e)
Em 1 e 4.
(a) [0,6] A intensidade de corrrente elétrica I[S] através de uma superfı́cie S e a densidade de corrente elétrica
~ , estão relacionadas por
nela, J
Z
~ · n̂ dA .
I[S] =
J
(f)
Em 2 e 3.
Logo, para uma seção reta do fio interno, temos
(g)
Em nenhuma surgirá corrente induzida, pois o
campo gerado pelo fio, mantém-se estacionário
e a ŕea do retângulo não varia.
S
Iint =
=
Z
ZSint
Crẑ · ẑ dA
Cr 2πr dr
Sint
Seção 2. Questões discursivas (2×2,6 = 5,2 pontos)
= 2πC
Todas as respostas devem ter justificativas!
1. [2,6 pontos] Um cabo coaxial é composto por um fio sólido, cilı́ndrico, circular, de raio R, envolto por uma casca
espessa, cilı́ndrica, também circular, coaxial, de raios a e b, tais que R < a < b. Ambos os cilindros são muito
longos e têm o eixo comum Z. Através do fio interno, passa uma corrente elétrica estacionária, cuja densidade de
~ int = Cr ẑ, onde C = const > 0 e r é a distância até o eixo do fio. Através da casca externa,
corrente é dada por J
~ ext = −J0 ẑ, onde J0 = const > 0.
passa uma corrente estacionária, cuja densidade de corrente é dada por J
3
Z
R
r 2 dr ,
r=0
ou seja,
2
Iint = πCR3 .
3
4
(1)
(b) [0,4] Na casca externa, temos
Iext =
• R ≤ r ≤ a: nesse caso, a corrente encerrada Ienc (r) é dada pela corrente toda do fio interno, ou seja, pela
Eq. (1):
Z
Jext · n̂ dA
Ienc (r) = Iint
2
= πCR3 .
3
ZSext
(−J0 ẑ) · ẑ dA
Z
= −J0
dA
=
Sext
Então, pela lei de Ampère, vem
Sext
2
Bϕ (r)2πr = µ0 πCR3 ,
3
= −J0 Aext ,
ou seja,
Iext = −J0 π(b2 − a2 ) .
e, finalmente,
(2)
3
~ = µ0 Iint ϕ̂ = 1 µ0 CR ϕ̂ .
B
2πr
3 r
(c) [1,6] Devido à simetria cilı́ndrica da distribuição estacionária de corrente e à lei de Gauss do magnetismo, em
qualquer uma das quatro regiões, o campo magnético, só terá componente azimutal (circular), ou seja,2
• a ≤ r ≤ b: nesse caso, a corrente encerrada Ienc (r) é dada pela corrente do fio interno mais a corrente na casca
externa, Eq, (2), contanto que, nessa última, troquemos b por r, ou seja:
~
B(r,
ϕ) = Bϕ (r) ϕ̂(ϕ) .
Ienc (r) = Iint + Iext (r)
2
= πCR3 − J0 π(r 2 − a2 ) .
3
Isso tudo sugere, pois, que usemos a lei de Ampère e que tomemos, como curva ampèriana, uma circunferência de
cı́rculo, concêntrico com o eixo da distribuição de corrente e perpendicular ao seu eixo, de raio genérico r. Assim,
a expressão funcional para a circulação do campo magnético ao longo da ampériana fica, em qualquer uma das
quatro regiões, igual a
I
~ · dℓ
ΓB
B
~ [C] :=
C
I
Bϕ (r) ϕ̂(ϕ) · dℓϕ ϕ̂
=
IC
=
Bϕ (r)dℓϕ
C
I
= Bϕ (r) dℓϕ ,
Então, pela lei de Ampère, vem
2
3
2
2
Bϕ (r)2πr = µ0 π πCR − J0 (r − a ) ,
3
e, finalmente,
1 CR3 1
a2
~
B = µ0
− J0 r −
ϕ̂ .
3 r
2
r
• b ≤ r < ∞: nesse caso, a corrente encerrada Ienc (r) é dada pela corrente total, Eq. (1) + Eq. (2), do fio interno
mais a corrente na casca externa, ou seja:
C
ou seja,
Ienc (r) = Iint + Iext .
ΓB
~ [C] = 2πrBϕ (r) .
Então, pela lei de Ampère, vem
A intensidade de corrente encerrada pela curva ampèriana dependerá, contudo, da região em questão. De fato,
Bϕ (r)2πr = µ0 (Iint + Iext ) ,
• 0 ≤ r ≤ R: nesse caso, a corrente encerrada Ienc (r) é dada pela Eq. (1), contanto que, nela, troquemos R por
r, ou seja:
Ienc (r) = Iint (r)
2
= πCr 3 .
3
Então, pela lei de Ampère, vem
2
Bϕ (r)2πr = µ0 πCr 3 ,
3
e, finalmente,
~ = 1 µ0 Cr 2 ϕ̂ .
B
3
2
A rigor, ainda poderia haver uma componente axial constante, que, suporemos nula, como usual.
5
e, finalmente,
~ = µ0 Iint + Iext ϕ̂ .
B
2πr
2. [2,6 pontos] Um pedaço de fio condutor ôhmico isolado é torcido de modo a constituir um circuito em forma de
oito. Por razão de simplicidade, modele as duas metades da figura de oito como circunferências de cı́rculo. O
raio do cı́rculo superior é a e o do inferior é 2a. O circuito completo é puramente resistivo (com capacitância e
auto-indutância desprezı́veis), tendo resistência R. A partir de t = 0 s, um campo magnético uniforme, mas não
estacionário,
~ = Ct ẑ ,
B
onde C = const > 0, é aplicado perpendicularmente ao plano dos dois cı́rculos, conforme mostrado na figura.
6
Então, o fluxo através do cı́rculo superior é
Φsup :=
Z
~ · n̂ dA
B
Ssup
=
Z
(Ctẑ) · n̂sup dA
Ssup
Z
(Ctẑ) · (−ẑ) dA
Z
dA
= −Ct
=
Ssup
;S sup
(a) Para t > 0 s, determine o fluxo total através do circuito. [1,2 ponto]
(b) Para t > 0 s, determine o sentido da corrente elétrica induzida ao longo do fio, indicando-o claramente em
cada uma das circunferências, seja por intermédio de uma seta, seja pelas expressões horário ou anti-horário.
[0,6 ponto]
(c) Para t > 0 s, determine o módulo da intensidade da corrente elétrica induzida no fio. [0,8 ponto]
Resolução:
= −CtAsup
= −πCta2 .
Analgoamente, para o fluxo através do cı́rculo inferior, temos
Φinf = CtAinf
= 4πCta2 .
Logo, o fluxo total através do circuito é
(a) [1,2] Tomaremos como orientação positiva da curva C que modela o circuito aquela indicada na figura, de modo
que os versores nas suas partes inferior e superior são dados por
Φ = Φsup + Φinf
ou seja,
Φ = 3πCa2 t .
(3)
(b) [0,6 ponto] Como, nitidamente, o módulo do fluxo está aumentando e a maior contribuição para ele vem do
cı́rculo inferior, deverá surgir, pela lei de Lenz, uma corrente induzida que parcialmente cancelará, por intermédio
do correspondente campo magnético “induzido”, no centro do cı́rculo inferior, o campo magnético externo. Isso
implica que a corrente induzida terá o sentido indicado pelas setas na figura a seguir, ou ainda,
• circunferência inferior: sentido horário
• circunferência superior: sentido anti-horário .
n̂sup = −ẑ
n̂inf = ẑ .
7
8
(c) [0,8] Pela lei de Faraday, temos que a força eletromotriz (fem) induzida ao longo do circuito é, tendo em vista
a Eq. (3),
Universidade Federal do Rio de Janeiro – Instituto de Fı́sica
Fı́sica III – 2014/1 – Segunda Prova: 12/05/2014
Teste
VERSÃO: C
dΦ
dt
= −3πCa2 .
Eind [C] = −
Como o circuito é puramente resistivo e satisfaz a lei de Ohm, temos que a corrente elétrica induzida vale
Iind =
Eind
,
R
Formulário
ou seja,
2
|Iind | =
3πCa
.
R
~ m = q~v × B
~ ,
F
I
~ m = Id~ℓ × B
~ ,
dF
~ ·dA
~ = 0,
B
~ =
dB
S
I
Seção 1.
~ d~ℓ = µ0 Ienc + µ0 ǫ0 dΦE ,
B·
dt
C
Eind = −
Múltipla escolha (8×0,6 = 4,8 pontos)
1. Um capacitor de placas paralelas, circulares e cujo
raio das placas é muito maior que a distância entre as
mesmas está inicialmente descarregado. A partir de
um certo instante, o capacitor começa a ser carregado
por uma corrente que cresce linearmente com o tempo
i(t) = bt, onde b = const > 0. Sobre os campos
elétrico e magnético que podem eventualmente surgir
entre as placas durante o carregamento do capacitor
pode-se afirmar que:
9
(a)
surgirá apenas um campo elétrico estacionário.
(b)
surgirão um campo elétrico estacionário e um
campo magnético não estacionário, colineares
entre si.
(c)
surgirá apenas um campo elétrico não estacionário.
(d)
surgirão um campo elétrico não estacionário e
um campo magnético estacionário, colineares
entre si.
(e)
surgirão um campo elétrico não estacionário e
um campo magnético estacionário, perpendiculares entre si.
(f)
surgirão um campo elétrico e um campo
magnético, ambos não estacionários, e perpendiculares entre si.
1
dΦB
,
dt
ΦB = LI ,
µ0 Id~ℓ × r̂
,
4π
r2
uB =
1 B2
.
2 µ0
2. Por um fio retilı́neo, muito longo, em repouso, passa
uma corrente elétrica estacionária de intensidade I.
Próximo a tal fio, há um retângulo condutor, rı́gido,
coplanar com o fio, conforme mostra a figura. Originalmente, o retângulo também encontra-se em repouso, mas, em um certo instante, ele passa a se movimentar em uma das quatro maneiras seguintes: (1)
translação com velocidade ~v 1 = v1 ŷ; (2) translação
com velocidade ~v 2 = v2 x̂; (3) translação com velocidade ~v 3 = v3x x̂ + v3y ŷ, ou (4) rotação (rı́gida) em
torno do eixo do próprio fio, com velocidade angular
~ = ωẑ. Em qual(is) das quatro situações, não surge
ω
uma corrente elétrica induzida ao longo do retângulo?
(a)
Somente em 1.
(b)
Somente em 4.
(c)
Somente em 2.
(d)
3. Calcule a força magnética resultante sobre o pedaço
de fio, através do qual passa uma corrente elétrica
estacionária de intensidade I, composto por dois segmentos retilı́neos, de comprimento L, muito grande, e
uma semicircunferência de cı́rculo, de raio a, na presença de um campo magnético constante (estacionário
~ = B ŷ, B = const > 0 .
e uniforme) B
(a)
2IaB ẑ .
(b)
−2IaB ẑ .
(c)
2ILB ẑ .
(d)
−2ILB ẑ .
(e)
2I(a + L)B ẑ .
(f)
−2I(a + L)B ẑ .
(g)
2I(a − L)B ẑ .
(h)
−2I(a − L)B ẑ .
Somente em 3.
(e)
Em 1 e 4.
(f)
Em 2 e 3.
(g)
Em nenhuma surgirá corrente induzida, pois o
campo gerado pelo fio, mantém-se estacionário
e a ŕea do retângulo não varia.
4. Uma barra de comprimento a ocupa uma região onde
há um campo magnético constante (estacionário e uni~ A barra gira com velocidade angular ω
~,
forme) B.
em torno de um ponto fixo em uma de suas extremidades, em um plano perpendicular ao campo. Qual
é o módulo da tensão ou da diferença de potencial
que acaba se estabelecendo entre as extremidades da
barra?
2
(a)
ωa2 B/4 .
(b)
2ωa2B .
(c)
ωa2 B .
(d)
ωa2 B/2 .
(e)
2πωa2B .
(f)
πωa2B .
(g)
0.
7. Calcule o campo magnético no ponto P devido ao circuito com corrente estacionária de intensidade I.
µ0 I 1 1
(a) −
−
ẑ .
4
a b
µ0 I 1 1
(b)
−
ẑ .
4
a b
µ0 I 1 1
ẑ .
−
(c) −
2
a b
µ0 I 1 1
(d)
ẑ .
−
2
a b
µ0 I 1 1
(e) −
−
ẑ .
2π a b
µ0 I 1 1
−
ẑ .
(f)
2π a b
µ0 I 1 1
(g) −
−
ẑ .
4π a b
µ0 I 1 1
−
ẑ .
(h)
4π a b
5. Considere as seguintes três afirmações sobre a lei de
Ampère: (I) ela só vale quando há um alto grau de
simetria da distribuição de correntes; (II) ela só vale
quando as correntes forem estacionárias, e (III) ela
só vale quando os campos magnéticos forem estacionários. Assinale a alternativa que indica qual(is)
de tais afirmações é(são) correta(s).
(a)
Nenhuma afirmação é correta.
(b)
Somente a I.
(c)
Somente a II.
(d)
Somente a III.
(e)
Somente a I e a II.
(f)
Somente a I e a III.
(g)
Somente a II e a III.
(h)
Todas as afirmações são corretas.
6. Seja um solenóide longo, formado por um enrolamento
de espiras circulares. Considere as seguintes três afirmativas sobre sua auto-indutância: (I) ela é proporcional ao quadrado do raio das espiras; (II) ela é proporcional à taxa de variação da corrente no solenóide,
e (III) ela é proporcional à corrente que circula no solenóide. Assinale a opção que indica qual(is) dessas
afirmativas está(ão) correta(s).
8. Todas as partı́culas carregadas que passam através
de uma região em que existem campos elétrico e
magnético constantes, ortogonais, sem serem defletidas têm em comum
(a)
Nenhuma das afirmativas está correta.
(a)
a massa.
(b)
Apenas a I.
(b)
o momento linear.
a velocidade.
(c)
Apenas a II.
(c)
(d)
Apenas a III.
(d)
a energia.
(e)
Apenas a I e a II.
(e)
a razão entre carga e massa.
(f)
Apenas a I e a III.
(g)
Apenas a II e a III.
(h)
Todas as afirmativas estão corretas.
Seção 2. Questões discursivas (2×2,6 = 5,2 pontos)
Todas as respostas devem ter justificativas!
1. [2,6 pontos] Um cabo coaxial é composto por um fio sólido, cilı́ndrico, circular, de raio R, envolto por uma casca
espessa, cilı́ndrica, também circular, coaxial, de raios a e b, tais que R < a < b. Ambos os cilindros são muito
longos e têm o eixo comum Z. Através do fio interno, passa uma corrente elétrica estacionária, cuja densidade de
~ int = Cr ẑ, onde C = const > 0 e r é a distância até o eixo do fio. Através da casca externa,
corrente é dada por J
~ ext = −J0 ẑ, onde J0 = const > 0.
passa uma corrente estacionária, cuja densidade de corrente é dada por J
3
Gabarito para Versão C
Seção 1.
Múltipla escolha (8×0,6 = 4,8 pontos)
1. Um capacitor de placas paralelas, circulares e cujo
raio das placas é muito maior que a distância entre as
mesmas está inicialmente descarregado. A partir de
um certo instante, o capacitor começa a ser carregado
por uma corrente que cresce linearmente com o tempo
i(t) = bt, onde b = const > 0. Sobre os campos
elétrico e magnético que podem eventualmente surgir
entre as placas durante o carregamento do capacitor
pode-se afirmar que:
(a) Qual é a (intensidade de) corrente elétrica no fio interno? [0,6 ponto]
(b) Qual é a (intensidade de) corrente elétrica na casca externa? [0,4 ponto]
~ em cada uma das quatro regiões em que o cabo “divide” o espaço. [1,6 ponto]
(c) Determine o campo magnético B
2. [2,6 pontos] Um pedaço de fio condutor ôhmico isolado é torcido de modo a constituir um circuito em forma de
oito. Por razão de simplicidade, modele as duas metades da figura de oito como circunferências de cı́rculo. O
raio do cı́rculo superior é a e o do inferior é 2a. O circuito completo é puramente resistivo (com capacitância e
auto-indutância desprezı́veis), tendo resistência R. A partir de t = 0 s, um campo magnético uniforme, mas não
estacionário,
~ = Ct ẑ ,
B
(a)
surgirá apenas um campo elétrico estacionário.
(b)
surgirão um campo elétrico estacionário e um
campo magnético não estacionário, colineares
entre si.
(c)
surgirá apenas um campo elétrico não estacionário.
(d)
surgirão um campo elétrico não estacionário e
um campo magnético estacionário, colineares
entre si.
(e)
surgirão um campo elétrico não estacionário e
um campo magnético estacionário, perpendiculares entre si.
surgirão um campo elétrico e um campo
magnético, ambos não estacionários, e perpendiculares entre si.
(f)
2. Por um fio retilı́neo, muito longo, em repouso, passa
uma corrente elétrica estacionária de intensidade I.
Próximo a tal fio, há um retângulo condutor, rı́gido,
coplanar com o fio, conforme mostra a figura. Originalmente, o retângulo também encontra-se em repouso, mas, em um certo instante, ele passa a se movimentar em uma das quatro maneiras seguintes: (1)
translação com velocidade ~v 1 = v1 ŷ; (2) translação
com velocidade ~v 2 = v2 x̂; (3) translação com velocidade ~v 3 = v3x x̂ + v3y ŷ, ou (4) rotação (rı́gida) em
torno do eixo do próprio fio, com velocidade angular
~ = ωẑ. Em qual(is) das quatro situações, não surge
ω
uma corrente elétrica induzida ao longo do retângulo?
onde C = const > 0, é aplicado perpendicularmente ao plano dos dois cı́rculos, conforme mostrado na figura.
(a) Para t > 0 s, determine o fluxo total através do circuito. [1,2 ponto]
(b) Para t > 0 s, determine o sentido da corrente elétrica induzida ao longo do fio, indicando-o claramente em
cada uma das circunferências, seja por intermédio de uma seta, seja pelas expressões horário ou anti-horário.
[0,6 ponto]
(c) Para t > 0 s, determine o módulo da intensidade da corrente elétrica induzida no fio. [0,8 ponto]
4
1
(a)
Somente em 1.
(b)
Somente em 4.
(c)
Somente em 2.
(d)
Somente em 3.
(e)
Em 1 e 4.
(f)
Em 2 e 3.
(g)
Em nenhuma surgirá corrente induzida, pois o
campo gerado pelo fio, mantém-se estacionário
e a ŕea do retângulo não varia.
5. Considere as seguintes três afirmações sobre a lei de
Ampère: (I) ela só vale quando há um alto grau de
simetria da distribuição de correntes; (II) ela só vale
quando as correntes forem estacionárias, e (III) ela
só vale quando os campos magnéticos forem estacionários. Assinale a alternativa que indica qual(is)
de tais afirmações é(são) correta(s).
3. Calcule a força magnética resultante sobre o pedaço
de fio, através do qual passa uma corrente elétrica
estacionária de intensidade I, composto por dois segmentos retilı́neos, de comprimento L, muito grande, e
uma semicircunferência de cı́rculo, de raio a, na presença de um campo magnético constante (estacionário
~ = B ŷ, B = const > 0 .
e uniforme) B
(a)
2IaB ẑ .
(b)
−2IaB ẑ .
(c)
2ILB ẑ .
(d)
−2ILB ẑ .
(e)
2I(a + L)B ẑ .
(f)
−2I(a + L)B ẑ .
(g)
2I(a − L)B ẑ .
(h)
−2I(a − L)B ẑ .
(a)
Nenhuma afirmação é correta.
(b)
Somente a I.
(c)
Somente a II.
(d)
Somente a III.
(e)
Somente a I e a II.
(f)
Somente a I e a III.
(g)
Somente a II e a III.
(h)
Todas as afirmações são corretas.
7. Calcule o campo magnético no ponto P devido ao circuito com corrente estacionária de intensidade I.
µ0 I 1 1
(a) −
−
ẑ .
4
a b
µ0 I 1 1
ẑ .
−
(b)
4
a b
µ0 I 1 1
−
ẑ .
(c) −
2
a b
µ0 I 1 1
(d)
−
ẑ .
2
a b
µ0 I 1 1
(e) −
ẑ .
−
2π a b
µ0 I 1 1
(f)
ẑ .
−
2π a b
µ0 I 1 1
−
ẑ .
(g) −
4π a b
µ0 I 1 1
(h)
−
ẑ .
4π a b
8. Todas as partı́culas carregadas que passam através
de uma região em que existem campos elétrico e
magnético constantes, ortogonais, sem serem defletidas têm em comum
(a)
a massa.
(b)
o momento linear.
(c)
a velocidade.
(d)
a energia.
(e)
a razão entre carga e massa.
Seção 2. Questões discursivas (2×2,6 = 5,2 pontos)
Todas as respostas devem ter justificativas!
1. [2,6 pontos] Um cabo coaxial é composto por um fio sólido, cilı́ndrico, circular, de raio R, envolto por uma casca
espessa, cilı́ndrica, também circular, coaxial, de raios a e b, tais que R < a < b. Ambos os cilindros são muito
longos e têm o eixo comum Z. Através do fio interno, passa uma corrente elétrica estacionária, cuja densidade de
~ int = Cr ẑ, onde C = const > 0 e r é a distância até o eixo do fio. Através da casca externa,
corrente é dada por J
~ ext = −J0 ẑ, onde J0 = const > 0.
passa uma corrente estacionária, cuja densidade de corrente é dada por J
6. Seja um solenóide longo, formado por um enrolamento
de espiras circulares. Considere as seguintes três afirmativas sobre sua auto-indutância: (I) ela é proporcional ao quadrado do raio das espiras; (II) ela é proporcional à taxa de variação da corrente no solenóide,
e (III) ela é proporcional à corrente que circula no solenóide. Assinale a opção que indica qual(is) dessas
afirmativas está(ão) correta(s).
4. Uma barra de comprimento a ocupa uma região onde
há um campo magnético constante (estacionário e uni~ A barra gira com velocidade angular ω
~,
forme) B.
em torno de um ponto fixo em uma de suas extremidades, em um plano perpendicular ao campo. Qual
é o módulo da tensão ou da diferença de potencial
que acaba se estabelecendo entre as extremidades da
barra?
(a)
Nenhuma das afirmativas está correta.
(a)
ωa2 B/4 .
(b)
Apenas a I.
(b)
2ωa2 B .
(c)
Apenas a II.
(c)
ωa B .
(d)
Apenas a III.
(d)
ωa2 B/2 .
(e)
Apenas a I e a II.
2
2
(e)
2πωa B .
(f)
Apenas a I e a III.
(f)
2
πωa B .
(g)
Apenas a II e a III.
(g)
0.
(h)
Todas as afirmativas estão corretas.
2
3
(b) [0,4] Na casca externa, temos
Iext =
Z
Jext · n̂ dA
ZSext
(−J0 ẑ) · ẑ dA
Z
= −J0
dA
=
Sext
Sext
= −J0 Aext ,
ou seja,
Iext = −J0 π(b2 − a2 ) .
(2)
(c) [1,6] Devido à simetria cilı́ndrica da distribuição estacionária de corrente e à lei de Gauss do magnetismo, em
qualquer uma das quatro regiões, o campo magnético, só terá componente azimutal (circular), ou seja,3
~
B(r,
ϕ) = Bϕ (r) ϕ̂(ϕ) .
(a) [0,6] A intensidade de corrrente elétrica I[S] através de uma superfı́cie S e a densidade de corrente elétrica
~ , estão relacionadas por
nela, J
Z
~ · n̂ dA .
I[S] =
J
Isso tudo sugere, pois, que usemos a lei de Ampère e que tomemos, como curva ampèriana, uma circunferência de
cı́rculo, concêntrico com o eixo da distribuição de corrente e perpendicular ao seu eixo, de raio genérico r. Assim,
a expressão funcional para a circulação do campo magnético ao longo da ampériana fica, em qualquer uma das
quatro regiões, igual a
I
~ · dℓ
ΓB
B
~ [C] :=
C
I
Bϕ (r) ϕ̂(ϕ) · dℓϕ ϕ̂
=
IC
=
Bϕ (r)dℓϕ
C
I
= Bϕ (r) dℓϕ ,
Logo, para uma seção reta do fio interno, temos
ou seja,
(a) Qual é a (intensidade de) corrente elétrica no fio interno? [0,6 ponto]
(b) Qual é a (intensidade de) corrente elétrica na casca externa? [0,4 ponto]
~ em cada uma das quatro regiões em que o cabo “divide” o espaço. [1,6 ponto]
(c) Determine o campo magnético B
Resolução:
S
Iint =
=
Z
ZSint
C
ΓB
~ [C] = 2πrBϕ (r) .
Crẑ · ẑ dA
A intensidade de corrente encerrada pela curva ampèriana dependerá, contudo, da região em questão. De fato,
• 0 ≤ r ≤ R: nesse caso, a corrente encerrada Ienc (r) é dada pela Eq. (1), contanto que, nela, troquemos R por
r, ou seja:
Cr 2πr dr
Sint
= 2πC
Z
R
r 2 dr ,
Ienc (r) = Iint (r)
2
= πCr 3 .
3
r=0
ou seja,
2
Iint = πCR3 .
3
Então, pela lei de Ampère, vem
(1)
2
Bϕ (r)2πr = µ0 πCr 3 ,
3
e, finalmente,
~ = 1 µ0 Cr 2 ϕ̂ .
B
3
3
4
A rigor, ainda poderia haver uma componente axial constante, que, suporemos nula, como usual.
5
• R ≤ r ≤ a: nesse caso, a corrente encerrada Ienc (r) é dada pela corrente toda do fio interno, ou seja, pela
Eq. (1):
Ienc (r) = Iint
2
= πCR3 .
3
Então, pela lei de Ampère, vem
2
Bϕ (r)2πr = µ0 πCR3 ,
3
e, finalmente,
3
~ = µ0 Iint ϕ̂ = 1 µ0 CR ϕ̂ .
B
2πr
3 r
• a ≤ r ≤ b: nesse caso, a corrente encerrada Ienc (r) é dada pela corrente do fio interno mais a corrente na casca
externa, Eq, (2), contanto que, nessa última, troquemos b por r, ou seja:
Ienc (r) = Iint + Iext (r)
2
= πCR3 − J0 π(r 2 − a2 ) .
3
(a) Para t > 0 s, determine o fluxo total através do circuito. [1,2 ponto]
(b) Para t > 0 s, determine o sentido da corrente elétrica induzida ao longo do fio, indicando-o claramente em
cada uma das circunferências, seja por intermédio de uma seta, seja pelas expressões horário ou anti-horário.
[0,6 ponto]
(c) Para t > 0 s, determine o módulo da intensidade da corrente elétrica induzida no fio. [0,8 ponto]
Resolução:
(a) [1,2] Tomaremos como orientação positiva da curva C que modela o circuito aquela indicada na figura, de modo
que os versores nas suas partes inferior e superior são dados por
Então, pela lei de Ampère, vem
2
3
2
2
Bϕ (r)2πr = µ0 π πCR − J0 (r − a ) ,
3
e, finalmente,
1 CR3 1
a2
~
B = µ0
− J0 r −
ϕ̂ .
3 r
2
r
• b ≤ r < ∞: nesse caso, a corrente encerrada Ienc (r) é dada pela corrente total, Eq. (1) + Eq. (2), do fio interno
mais a corrente na casca externa, ou seja:
Ienc (r) = Iint + Iext .
Então, pela lei de Ampère, vem
Bϕ (r)2πr = µ0 (Iint + Iext ) ,
e, finalmente,
~ = µ0 Iint + Iext ϕ̂ .
B
2πr
n̂sup = −ẑ
n̂inf = ẑ .
2. [2,6 pontos] Um pedaço de fio condutor ôhmico isolado é torcido de modo a constituir um circuito em forma de
oito. Por razão de simplicidade, modele as duas metades da figura de oito como circunferências de cı́rculo. O
raio do cı́rculo superior é a e o do inferior é 2a. O circuito completo é puramente resistivo (com capacitância e
auto-indutância desprezı́veis), tendo resistência R. A partir de t = 0 s, um campo magnético uniforme, mas não
estacionário,
~ = Ct ẑ ,
B
onde C = const > 0, é aplicado perpendicularmente ao plano dos dois cı́rculos, conforme mostrado na figura.
6
7
Então, o fluxo através do cı́rculo superior é
Φsup :=
(c) [0,8] Pela lei de Faraday, temos que a força eletromotriz (fem) induzida ao longo do circuito é, tendo em vista
a Eq. (3),
Z
~ · n̂ dA
B
dΦ
dt
= −3πCa2 .
Ssup
=
Z
Eind [C] = −
(Ctẑ) · n̂sup dA
Ssup
Z
(Ctẑ) · (−ẑ) dA
Z
dA
= −Ct
Como o circuito é puramente resistivo e satisfaz a lei de Ohm, temos que a corrente elétrica induzida vale
= −CtAsup
= −πCta2 .
ou seja,
=
Ssup
Iind =
;S sup
|Iind | =
Analgoamente, para o fluxo através do cı́rculo inferior, temos
Φinf = CtAinf
= 4πCta2 .
Logo, o fluxo total através do circuito é
Φ = Φsup + Φinf
ou seja,
Φ = 3πCa2 t .
(3)
(b) [0,6 ponto] Como, nitidamente, o módulo do fluxo está aumentando e a maior contribuição para ele vem do
cı́rculo inferior, deverá surgir, pela lei de Lenz, uma corrente induzida que parcialmente cancelará, por intermédio
do correspondente campo magnético “induzido”, no centro do cı́rculo inferior, o campo magnético externo. Isso
implica que a corrente induzida terá o sentido indicado pelas setas na figura a seguir, ou ainda,
• circunferência inferior: sentido horário
• circunferência superior: sentido anti-horário .
8
9
Eind
,
R
3πCa2
.
R
Universidade Federal do Rio de Janeiro – Instituto de Fı́sica
Fı́sica III – 2014/1 – Segunda Prova: 12/05/2014
Teste
VERSÃO: D
Formulário
~ m = q~v × B
~ ,
F
I
~ m = Id~ℓ × B
~ ,
dF
~ ·dA
~ = 0,
B
~ =
dB
S
I
Seção 1.
~ d~ℓ = µ0 Ienc + µ0 ǫ0 dΦE ,
B·
dt
C
Eind
dΦB
=−
,
dt
ΦB = LI ,
µ0 Id~ℓ × r̂
,
4π
r2
1 B2
uB =
.
2 µ0
(a)
ωa2 B/4 .
(b)
2ωa2 B .
(c)
ωa2 B .
(d)
ωa2 B/2 .
(e)
2πωa2 B .
(f)
πωa2 B .
(g)
0.
4. Todas as partı́culas carregadas que passam através
de uma região em que existem campos elétrico e
magnético constantes, ortogonais, sem serem defletidas têm em comum
Múltipla escolha (8×0,6 = 4,8 pontos)
1. Calcule a força magnética resultante sobre o pedaço
de fio, através do qual passa uma corrente elétrica
estacionária de intensidade I, composto por dois segmentos retilı́neos, de comprimento L, muito grande, e
uma semicircunferência de cı́rculo, de raio a, na presença de um campo magnético constante (estacionário
~ = B ŷ, B = const > 0 .
e uniforme) B
2. Calcule o campo magnético no ponto P devido ao circuito com corrente estacionária de intensidade I.
µ0 I 1 1
(a) −
ẑ .
−
4
a b
µ0 I 1 1
−
ẑ .
(b)
4
a b
µ0 I 1 1
(c) −
−
ẑ .
2
a b
µ0 I 1 1
(d)
ẑ .
−
2
a b
µ0 I 1 1
ẑ .
−
(e) −
2π a b
µ0 I 1 1
(f)
−
ẑ .
2π a b
µ0 I 1 1
−
ẑ .
(g) −
4π a b
µ0 I 1 1
(h)
−
ẑ .
4π a b
(a)
a massa.
(b)
o momento linear.
(a)
Somente em 1.
(c)
a velocidade.
(b)
Somente em 4.
(d)
a energia.
(c)
Somente em 2.
(e)
a razão entre carga e massa.
(d)
Somente em 3.
(e)
Em 1 e 4.
(f)
Em 2 e 3.
(g)
Em nenhuma surgirá corrente induzida, pois o
campo gerado pelo fio, mantém-se estacionário
e a ŕea do retângulo não varia.
5. Considere as seguintes três afirmações sobre a lei de
Ampère: (I) ela só vale quando há um alto grau de
simetria da distribuição de correntes; (II) ela só vale
quando as correntes forem estacionárias, e (III) ela
só vale quando os campos magnéticos forem estacionários. Assinale a alternativa que indica qual(is)
de tais afirmações é(são) correta(s).
(a)
Nenhuma afirmação é correta.
(b)
Somente a I.
(c)
Somente a II.
(d)
Somente a III.
(e)
Somente a I e a II.
2I(a + L)B ẑ .
(f)
Somente a I e a III.
−2I(a + L)B ẑ .
(g)
Somente a II e a III.
(g)
2I(a − L)B ẑ .
(h)
Todas as afirmações são corretas.
(h)
−2I(a − L)B ẑ .
(a)
2IaB ẑ .
(b)
−2IaB ẑ .
(c)
2ILB ẑ .
(d)
−2ILB ẑ .
(e)
(f)
6. Por um fio retilı́neo, muito longo, em repouso, passa
uma corrente elétrica estacionária de intensidade I.
Próximo a tal fio, há um retângulo condutor, rı́gido,
coplanar com o fio, conforme mostra a figura. Originalmente, o retângulo também encontra-se em repouso, mas, em um certo instante, ele passa a se movimentar em uma das quatro maneiras seguintes: (1)
translação com velocidade ~v 1 = v1 ŷ; (2) translação
com velocidade ~v 2 = v2 x̂; (3) translação com velocidade ~v 3 = v3x x̂ + v3y ŷ, ou (4) rotação (rı́gida) em
torno do eixo do próprio fio, com velocidade angular
~ = ωẑ. Em qual(is) das quatro situações, não surge
ω
uma corrente elétrica induzida ao longo do retângulo?
3. Uma barra de comprimento a ocupa uma região onde
há um campo magnético constante (estacionário e uni~ A barra gira com velocidade angular ω
~,
forme) B.
em torno de um ponto fixo em uma de suas extremidades, em um plano perpendicular ao campo. Qual
é o módulo da tensão ou da diferença de potencial
que acaba se estabelecendo entre as extremidades da
barra?
1
2
8. Seja um solenóide longo, formado por um enrolamento
de espiras circulares. Considere as seguintes três afirmativas sobre sua auto-indutância: (I) ela é proporcional ao quadrado do raio das espiras; (II) ela é proporcional à taxa de variação da corrente no solenóide,
e (III) ela é proporcional à corrente que circula no solenóide. Assinale a opção que indica qual(is) dessas
afirmativas está(ão) correta(s).
7. Um capacitor de placas paralelas, circulares e cujo
raio das placas é muito maior que a distância entre as
mesmas está inicialmente descarregado. A partir de
um certo instante, o capacitor começa a ser carregado
por uma corrente que cresce linearmente com o tempo
i(t) = bt, onde b = const > 0. Sobre os campos
elétrico e magnético que podem eventualmente surgir
entre as placas durante o carregamento do capacitor
pode-se afirmar que:
(a)
Nenhuma das afirmativas está correta.
(a)
surgirá apenas um campo elétrico estacionário.
(b)
Apenas a I.
(b)
surgirão um campo elétrico estacionário e um
campo magnético não estacionário, colineares
entre si.
(c)
Apenas a II.
(d)
Apenas a III.
Apenas a I e a II.
(c)
surgirá apenas um campo elétrico não estacionário.
(e)
(f)
Apenas a I e a III.
(d)
surgirão um campo elétrico não estacionário e
um campo magnético estacionário, colineares
entre si.
(g)
Apenas a II e a III.
(h)
Todas as afirmativas estão corretas.
(e)
(f)
surgirão um campo elétrico não estacionário e
um campo magnético estacionário, perpendiculares entre si.
(a) Qual é a (intensidade de) corrente elétrica no fio interno? [0,6 ponto]
(b) Qual é a (intensidade de) corrente elétrica na casca externa? [0,4 ponto]
~ em cada uma das quatro regiões em que o cabo “divide” o espaço. [1,6 ponto]
(c) Determine o campo magnético B
surgirão um campo elétrico e um campo
magnético, ambos não estacionários, e perpendiculares entre si.
Seção 2. Questões discursivas (2×2,6 = 5,2 pontos)
Todas as respostas devem ter justificativas!
1. [2,6 pontos] Um cabo coaxial é composto por um fio sólido, cilı́ndrico, circular, de raio R, envolto por uma casca
espessa, cilı́ndrica, também circular, coaxial, de raios a e b, tais que R < a < b. Ambos os cilindros são muito
longos e têm o eixo comum Z. Através do fio interno, passa uma corrente elétrica estacionária, cuja densidade de
~ int = Cr ẑ, onde C = const > 0 e r é a distância até o eixo do fio. Através da casca externa,
corrente é dada por J
~ ext = −J0 ẑ, onde J0 = const > 0.
passa uma corrente estacionária, cuja densidade de corrente é dada por J
2. [2,6 pontos] Um pedaço de fio condutor ôhmico isolado é torcido de modo a constituir um circuito em forma de
oito. Por razão de simplicidade, modele as duas metades da figura de oito como circunferências de cı́rculo. O
raio do cı́rculo superior é a e o do inferior é 2a. O circuito completo é puramente resistivo (com capacitância e
auto-indutância desprezı́veis), tendo resistência R. A partir de t = 0 s, um campo magnético uniforme, mas não
estacionário,
~ = Ct ẑ ,
B
onde C = const > 0, é aplicado perpendicularmente ao plano dos dois cı́rculos, conforme mostrado na figura.
(a) Para t > 0 s, determine o fluxo total através do circuito. [1,2 ponto]
(b) Para t > 0 s, determine o sentido da corrente elétrica induzida ao longo do fio, indicando-o claramente em
cada uma das circunferências, seja por intermédio de uma seta, seja pelas expressões horário ou anti-horário.
[0,6 ponto]
(c) Para t > 0 s, determine o módulo da intensidade da corrente elétrica induzida no fio. [0,8 ponto]
3
4
Seção 1.
Múltipla escolha (8×0,6 = 4,8 pontos)
1. Calcule a força magnética resultante sobre o pedaço
de fio, através do qual passa uma corrente elétrica
estacionária de intensidade I, composto por dois segmentos retilı́neos, de comprimento L, muito grande, e
uma semicircunferência de cı́rculo, de raio a, na presença de um campo magnético constante (estacionário
~ = B ŷ, B = const > 0 .
e uniforme) B
6. Por um fio retilı́neo, muito longo, em repouso, passa
uma corrente elétrica estacionária de intensidade I.
Próximo a tal fio, há um retângulo condutor, rı́gido,
coplanar com o fio, conforme mostra a figura. Originalmente, o retângulo também encontra-se em repouso, mas, em um certo instante, ele passa a se movimentar em uma das quatro maneiras seguintes: (1)
translação com velocidade ~v 1 = v1 ŷ; (2) translação
com velocidade ~v 2 = v2 x̂; (3) translação com velocidade ~v 3 = v3x x̂ + v3y ŷ, ou (4) rotação (rı́gida) em
torno do eixo do próprio fio, com velocidade angular
~ = ωẑ. Em qual(is) das quatro situações, não surge
ω
uma corrente elétrica induzida ao longo do retângulo?
4. Todas as partı́culas carregadas que passam através
de uma região em que existem campos elétrico e
magnético constantes, ortogonais, sem serem defletidas têm em comum
Gabarito para Versão D
2. Calcule o campo magnético no ponto P devido ao circuito com corrente estacionária de intensidade I.
µ0 I 1 1
(a) −
−
ẑ .
4
a b
µ0 I 1 1
(b)
−
ẑ .
4
a b
µ0 I 1 1
−
ẑ .
(c) −
2
a b
µ0 I 1 1
(d)
−
ẑ .
2
a b
µ0 I 1 1
−
ẑ .
(e) −
2π a b
µ0 I 1 1
(f)
−
ẑ .
2π a b
µ0 I 1 1
ẑ .
−
(g) −
4π a b
µ0 I 1 1
(h)
ẑ .
−
4π a b
(a)
a massa.
(b)
o momento linear.
(c)
a velocidade.
(d)
a energia.
(e)
a razão entre carga e massa.
(a)
2IaB ẑ .
(b)
−2IaB ẑ .
(c)
2ILB ẑ .
(d)
−2ILB ẑ .
(a)
Somente em 1.
(e)
2I(a + L)B ẑ .
(b)
Somente em 4.
(f)
−2I(a + L)B ẑ .
(c)
Somente em 2.
(g)
2I(a − L)B ẑ .
(d)
Somente em 3.
−2I(a − L)B ẑ .
(e)
Em 1 e 4.
(f)
Em 2 e 3.
(g)
Em nenhuma surgirá corrente induzida, pois o
campo gerado pelo fio, mantém-se estacionário
e a ŕea do retângulo não varia.
(h)
3. Uma barra de comprimento a ocupa uma região onde
há um campo magnético constante (estacionário e uni~ A barra gira com velocidade angular ω
~,
forme) B.
em torno de um ponto fixo em uma de suas extremidades, em um plano perpendicular ao campo. Qual
é o módulo da tensão ou da diferença de potencial
que acaba se estabelecendo entre as extremidades da
barra?
1
5. Considere as seguintes três afirmações sobre a lei de
Ampère: (I) ela só vale quando há um alto grau de
simetria da distribuição de correntes; (II) ela só vale
quando as correntes forem estacionárias, e (III) ela
só vale quando os campos magnéticos forem estacionários. Assinale a alternativa que indica qual(is)
de tais afirmações é(são) correta(s).
(a)
Nenhuma afirmação é correta.
(a)
ωa2 B/4 .
(b)
Somente a I.
(b)
2ωa2B .
(c)
Somente a II.
Somente a III.
2
(c)
ωa B .
(d)
(d)
ωa2 B/2 .
(e)
Somente a I e a II.
(e)
2πωa2B .
(f)
Somente a I e a III.
(f)
πωa2B .
(g)
Somente a II e a III.
(g)
0.
(h)
Todas as afirmações são corretas.
2
7. Um capacitor de placas paralelas, circulares e cujo
raio das placas é muito maior que a distância entre as
mesmas está inicialmente descarregado. A partir de
um certo instante, o capacitor começa a ser carregado
por uma corrente que cresce linearmente com o tempo
i(t) = bt, onde b = const > 0. Sobre os campos
elétrico e magnético que podem eventualmente surgir
entre as placas durante o carregamento do capacitor
pode-se afirmar que:
8. Seja um solenóide longo, formado por um enrolamento
de espiras circulares. Considere as seguintes três afirmativas sobre sua auto-indutância: (I) ela é proporcional ao quadrado do raio das espiras; (II) ela é proporcional à taxa de variação da corrente no solenóide,
e (III) ela é proporcional à corrente que circula no solenóide. Assinale a opção que indica qual(is) dessas
afirmativas está(ão) correta(s).
(a)
Nenhuma das afirmativas está correta.
(a)
surgirá apenas um campo elétrico estacionário.
(b)
Apenas a I.
(b)
surgirão um campo elétrico estacionário e um
campo magnético não estacionário, colineares
entre si.
(c)
Apenas a II.
(d)
Apenas a III.
(e)
Apenas a I e a II.
(f)
Apenas a I e a III.
(g)
Apenas a II e a III.
(h)
Todas as afirmativas estão corretas.
(c)
(d)
(e)
(f)
surgirá apenas um campo elétrico não estacionário.
surgirão um campo elétrico não estacionário e
um campo magnético estacionário, colineares
entre si.
surgirão um campo elétrico não estacionário e
um campo magnético estacionário, perpendiculares entre si.
surgirão um campo elétrico e um campo
magnético, ambos não estacionários, e perpendiculares entre si.
(a) Qual é a (intensidade de) corrente elétrica no fio interno? [0,6 ponto]
(b) Qual é a (intensidade de) corrente elétrica na casca externa? [0,4 ponto]
~ em cada uma das quatro regiões em que o cabo “divide” o espaço. [1,6 ponto]
(c) Determine o campo magnético B
Resolução:
Seção 2. Questões discursivas (2×2,6 = 5,2 pontos)
Todas as respostas devem ter justificativas!
1. [2,6 pontos] Um cabo coaxial é composto por um fio sólido, cilı́ndrico, circular, de raio R, envolto por uma casca
espessa, cilı́ndrica, também circular, coaxial, de raios a e b, tais que R < a < b. Ambos os cilindros são muito
longos e têm o eixo comum Z. Através do fio interno, passa uma corrente elétrica estacionária, cuja densidade de
~ int = Cr ẑ, onde C = const > 0 e r é a distância até o eixo do fio. Através da casca externa,
corrente é dada por J
~ ext = −J0 ẑ, onde J0 = const > 0.
passa uma corrente estacionária, cuja densidade de corrente é dada por J
(a) [0,6] A intensidade de corrrente elétrica I[S] através de uma superfı́cie S e a densidade de corrente elétrica
~ , estão relacionadas por
nela, J
Z
~ · n̂ dA .
I[S] =
J
S
Logo, para uma seção reta do fio interno, temos
Iint =
=
Z
ZSint
Crẑ · ẑ dA
Cr 2πr dr
Sint
= 2πC
Z
R
r 2 dr ,
r=0
ou seja,
2
Iint = πCR3 .
3
3
4
(1)
(b) [0,4] Na casca externa, temos
Iext =
• R ≤ r ≤ a: nesse caso, a corrente encerrada Ienc (r) é dada pela corrente toda do fio interno, ou seja, pela
Eq. (1):
Z
Jext · n̂ dA
Ienc (r) = Iint
2
= πCR3 .
3
ZSext
(−J0 ẑ) · ẑ dA
Z
= −J0
dA
=
Sext
Então, pela lei de Ampère, vem
Sext
2
Bϕ (r)2πr = µ0 πCR3 ,
3
= −J0 Aext ,
ou seja,
Iext = −J0 π(b2 − a2 ) .
e, finalmente,
(2)
3
~ = µ0 Iint ϕ̂ = 1 µ0 CR ϕ̂ .
B
2πr
3 r
(c) [1,6] Devido à simetria cilı́ndrica da distribuição estacionária de corrente e à lei de Gauss do magnetismo, em
qualquer uma das quatro regiões, o campo magnético, só terá componente azimutal (circular), ou seja,4
• a ≤ r ≤ b: nesse caso, a corrente encerrada Ienc (r) é dada pela corrente do fio interno mais a corrente na casca
externa, Eq, (2), contanto que, nessa última, troquemos b por r, ou seja:
~
B(r,
ϕ) = Bϕ (r) ϕ̂(ϕ) .
Ienc (r) = Iint + Iext (r)
2
= πCR3 − J0 π(r 2 − a2 ) .
3
Isso tudo sugere, pois, que usemos a lei de Ampère e que tomemos, como curva ampèriana, uma circunferência de
cı́rculo, concêntrico com o eixo da distribuição de corrente e perpendicular ao seu eixo, de raio genérico r. Assim,
a expressão funcional para a circulação do campo magnético ao longo da ampériana fica, em qualquer uma das
quatro regiões, igual a
I
~ · dℓ
ΓB
B
~ [C] :=
C
I
Bϕ (r) ϕ̂(ϕ) · dℓϕ ϕ̂
=
IC
=
Bϕ (r)dℓϕ
C
I
= Bϕ (r) dℓϕ ,
Então, pela lei de Ampère, vem
2
3
2
2
Bϕ (r)2πr = µ0 π πCR − J0 (r − a ) ,
3
e, finalmente,
1 CR3 1
a2
~
B = µ0
− J0 r −
ϕ̂ .
3 r
2
r
• b ≤ r < ∞: nesse caso, a corrente encerrada Ienc (r) é dada pela corrente total, Eq. (1) + Eq. (2), do fio interno
mais a corrente na casca externa, ou seja:
C
ou seja,
Ienc (r) = Iint + Iext .
ΓB
~ [C] = 2πrBϕ (r) .
Então, pela lei de Ampère, vem
A intensidade de corrente encerrada pela curva ampèriana dependerá, contudo, da região em questão. De fato,
Bϕ (r)2πr = µ0 (Iint + Iext ) ,
• 0 ≤ r ≤ R: nesse caso, a corrente encerrada Ienc (r) é dada pela Eq. (1), contanto que, nela, troquemos R por
r, ou seja:
Ienc (r) = Iint (r)
2
= πCr 3 .
3
Então, pela lei de Ampère, vem
2
Bϕ (r)2πr = µ0 πCr 3 ,
3
e, finalmente,
~ = 1 µ0 Cr 2 ϕ̂ .
B
3
4
A rigor, ainda poderia haver uma componente axial constante, que, suporemos nula, como usual.
5
e, finalmente,
~ = µ0 Iint + Iext ϕ̂ .
B
2πr
2. [2,6 pontos] Um pedaço de fio condutor ôhmico isolado é torcido de modo a constituir um circuito em forma de
oito. Por razão de simplicidade, modele as duas metades da figura de oito como circunferências de cı́rculo. O
raio do cı́rculo superior é a e o do inferior é 2a. O circuito completo é puramente resistivo (com capacitância e
auto-indutância desprezı́veis), tendo resistência R. A partir de t = 0 s, um campo magnético uniforme, mas não
estacionário,
~ = Ct ẑ ,
B
onde C = const > 0, é aplicado perpendicularmente ao plano dos dois cı́rculos, conforme mostrado na figura.
6
Então, o fluxo através do cı́rculo superior é
Φsup :=
Z
~ · n̂ dA
B
Ssup
=
Z
(Ctẑ) · n̂sup dA
Ssup
Z
(Ctẑ) · (−ẑ) dA
Z
dA
= −Ct
=
Ssup
;S sup
(a) Para t > 0 s, determine o fluxo total através do circuito. [1,2 ponto]
(b) Para t > 0 s, determine o sentido da corrente elétrica induzida ao longo do fio, indicando-o claramente em
cada uma das circunferências, seja por intermédio de uma seta, seja pelas expressões horário ou anti-horário.
[0,6 ponto]
(c) Para t > 0 s, determine o módulo da intensidade da corrente elétrica induzida no fio. [0,8 ponto]
Resolução:
= −CtAsup
= −πCta2 .
Analgoamente, para o fluxo através do cı́rculo inferior, temos
Φinf = CtAinf
= 4πCta2 .
Logo, o fluxo total através do circuito é
(a) [1,2] Tomaremos como orientação positiva da curva C que modela o circuito aquela indicada na figura, de modo
que os versores nas suas partes inferior e superior são dados por
Φ = Φsup + Φinf
ou seja,
Φ = 3πCa2 t .
(3)
(b) [0,6 ponto] Como, nitidamente, o módulo do fluxo está aumentando e a maior contribuição para ele vem do
cı́rculo inferior, deverá surgir, pela lei de Lenz, uma corrente induzida que parcialmente cancelará, por intermédio
do correspondente campo magnético “induzido”, no centro do cı́rculo inferior, o campo magnético externo. Isso
implica que a corrente induzida terá o sentido indicado pelas setas na figura a seguir, ou ainda,
• circunferência inferior: sentido horário
• circunferência superior: sentido anti-horário .
n̂sup = −ẑ
n̂inf = ẑ .
7
8
(c) [0,8] Pela lei de Faraday, temos que a força eletromotriz (fem) induzida ao longo do circuito é, tendo em vista
a Eq. (3),
dΦ
dt
= −3πCa2 .
Eind [C] = −
Como o circuito é puramente resistivo e satisfaz a lei de Ohm, temos que a corrente elétrica induzida vale
Iind =
Eind
,
R
ou seja,
|Iind | =
9
3πCa2
.
R