Exercícios sobre Cinemática - Departamento de Física

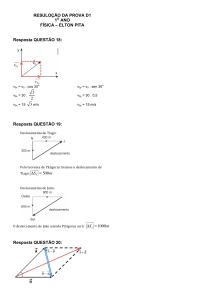
O valor negativo para τc deve ser descartado. Somando
este tempo aos 8 s da primeira etapa do movimento, o
tempo total de voo vale 13, 5 s.
EXERCÍCIOS DE CINEMÁTICA
UFPR – Departamento de Fı́sica
CF-345 – Fı́sica Básica I
2. A posição de uma partı́cula que se move em linha reta é
dada em função do tempo pela fórmula y(t) = 10 − α t2 +
β t3 , na qual o tempo é dado em segundos e a posição em
metros. α e β são constantes.
1. Um modelo de foguete disparado verticalmente do chão
se eleva com aceleração vertical constante de 2, 00 m/s2
por 8, 00 s. Seu combustı́vel então se esgota e ele continua
se deslocando para cima em “queda livre”, isto é, apenas
sob a ação da gravidade, e depois volta caindo.
(a) Determine as unidades de α e β.
(b) Determine os valores de α e β considerando que a
partı́cula inverte o sentido de seu movimento no instante
t = 1 s e que possui aceleração instantânea a = 18 m/s2
no instante t = 2 s.
Resolução
(a) Qual a altitude máxima alcançada?
(b) Qual o tempo total decorrido da decolagem até o
foguete bater no chão?
Resolução
(a) Adotaremos a origem do eixo vertical y, que aponta
pra cima, como sendo o nı́vel do chão. Começaremos a
contar o tempo a partir do lançamento, quando o foguete
está em repouso. O movimento ocorre em duas etapas
distintas.
(a) Para que a posição seja dada em metros, conforme o
enunciado, todos os termos do lado direito devem ter essa
unidade. Analisando o segundo termo, para que α t2 seja
dado em metros, sendo t dado em segundos, a unidade de
α deve ser m/s2 . Fazendo o mesmo para o último termo,
concluimos que a unidade de β é m/s3 .
Nos primeiros 8 s, o foguete é acelerado pra cima com
(1)
aceleração a1 = 2 m/s2 , a partir do repouso, vi = 0.
No final destes 8 s, a velocidade do foguete é
(b) Em primeiro lugar, vamos encontrar uma expressão
para a velocidade e aceleração da partı́cula a partir de
y(t):
(1)
(1)
vf = vi
+ a1 tf = (2 m/s2 ) × (8 s) = 16 m/s.
v(t)
a(t)
Neste instante tf também podemos calcular a posição do
foguete:
y
(1)
(tf ) =
=
(1)
yi
+
(1)
vi tf
(2)
2 m/s2
(8 s)2 = 64 m.
2
v(1) =
a(2) =
vi
= 1, 6 s.
g
(a) De acordo com a Fig. a, em que instantes, ou intervalos de tempo, a partı́cula se encontra parada? E quando
tem velocidade negativa ou positiva?
(b) Para o gráfico da Fig. a, esboce o gráfico da velocidade contra o tempo.
g
(2)
(2)
= yi + vi τ − τ 2
2
= 64 + 16 × 1, 6 − 5 × (1, 6)2 m
(c) De acordo com a Fig. b, a que distância da origem a
partı́cula se encontra em t = 15, 0 s?
= 76, 8 m.
(d) De acordo com a Fig. b, qual a velocidade média da
partı́cula entre os instantes t = 0, 0 s e t = 15, 0 s?
Resolução
Esta foi a altura máxima alcançada.
(b) Na segunda etapa, o instante τc em que o foguete
retorna ao chão é dado por
y
(2)
(τc ) =
(2)
yi
(2)
+
(2)
vi τc
−2α + 12β = 18.
3. Os gráficos da figura abaixo referem-se a movimentos
retilı́neos de uma partı́cula.
Nesse instante, nesta segunda etapa, sabendo que a
(2)
posição inicial é yi = y (1) (tf ) = 64 m, sua posição
vale
y (2) (τ )
−2α + 3β = 0,
Subtraindo a segunda equação da primeira: β = 2 m/s3 .
E, substituindo este valor na segunda, α = 3 m/s2 .
(2)
− gτ = 0 =⇒ τ =
= −2α + 6βt.
No instante em que a partı́cula inverte o sentido de movimento, sua velocidade necessariamente se anula, ou seja,
v(1) = 0. Além disso, do enunciado, a(2) = 18. Essas
duas informações nos levam ao sistema de equações:
a1
+ t2f
2
Depois disso, o foguete entra em outro regime de movimento, e voltamos a zerar o cronômetro. Ele está ini(2)
(1)
cialmente a uma velocidade vi = vf , e passa a ser
desacelerado pela gravidade, de modo que o instante τ ,
para o qual a ele atinge a altura máxima, é dado por
v(τ ) = vi
= −2αt + 3βt2 ,
(a) A partı́cula encontra-se parada quando a inclinação
do gráfico é nula: em t = 2, t = 4 e t ≥ 7. Quando
o gráfico tem inclinação positiva (negativa), a partı́cula
tem velocidade positiva (negativa). Portanto: a velocidade é positiva nos intervalos 0 ≤ t < 2 e 4 < t < 7, e é
negativa no intervalo 2 < t < 4.
g
− τc2 = 0
2
(2)
2vi
2y
τc − i = 0
g
g
2
=⇒ τc − 3, 2τc − 12, 8 = 0 =⇒ τc = 5, 5 s.
=⇒ τc2 −
1
Resolução
(a) Supondo, como pede-se no item (b), que a posição
xt do trem, em t = 0, vale xt (0) = 0, construı́mos as
seguintes equações para as posições xp (t) do passageiro
e xt (t) do trem:
xp (t) = −d + vm t
e
xt (t) =
1 2
at .
2
O passageiro somente será capaz de pegar o trem se existir um instante de tempo τ , tal que xp (τ ) = xt (τ ).
Segundo essa igualdade,
1 2
vm
d
aτ
=⇒ τ 2 − 2 τ + 2 = 0
2
a
a
r
2
vm
vm
d
=⇒ τ =
±
−2
a
a2
a
s
3, 1 m/s
(3, 1 m/s)2
12 m
τ=
±
−2×
2
2
2
0, 31 m/s
(0, 31 m/s )
0, 31 m/s2
√
≈ (10 ± 20) s.
−d + vm τ =
v (m /s)
(b) Veja o gráfico abaixo. O gráfico não deve entrar
em contradição com o que foi escrito no item anterior.
Também não deve ter “bicos” e a velocidade inicial não
deve ser zero.
Fazendo as contas, conclui-se que o passageiro, nesta
situação, tem duas oportunidades de pegar o trem: τ1 =
14, 47 s e τ2 = 5, 53 s.
(b) Veja os gráficos abaixo. (a) A função xt (t) deve ser
uma parábola e xp (t) deve ser uma reta. Variando os
valores de d, a função xp (t) varia, mas sem alterar sua
inclinação (a velocidade do passageiro não varia). Se a
distância inicial d for suficientemente pequena, o passageiro terá duas oportunidades de pegar o trem (existem dois pontos de intersecção entre xt (t) e xp (t)). Se
a distância inicial d for suficientemente grande, o passageiro não pegará o trem (não existem pontos de intersecção entre xt (t) e xp (t)). Existe um valor limite dc
para o qual existe somente um ponto de intersecção entre
xt (t) e xp (t). (b) Esse é o gráfico para quem considerou
xp (0) = 0. Uma discussão equivalente também deve ser
considerada.
0,0
0
1
2
3
4
5
6
7
8
9
10
t (s)
(c) A distância percorrida é equivalente à área entre a
curva e o eixo x:
5×5
∆x = 5×5
m = 50 m.
2 +5×5+ 2
(d) A velocidade média entre dois instantes de tempo é
dada por:
vm =
xf −xi
tf −ti
=
50 m
15 s
(a)
= (10/3) m/s.
posição (u .a.)
4. Um passageiro está correndo na sua velocidade máxima
vm = 3, 1 m/s para pegar um trem. Quando está a
uma distância d da entrada mais próxima do trem, este
começa a mover-se, do repouso, com aceleração constante
a = 0, 31 m/s2 , afastando-se do passageiro.
x t (t)
x p (t) com d c
x p (t) com ou tros d 's
(a) Quando d = 12 m, ele será capaz de pegar o trem?
tem po (u .a.)
(b) Faça o gráfico da função xt (t) do trem, escolhendo
xt = 0 quando t = 0. No mesmo gráfico, represente a
função xp (t) do passageiro com alguns valores iniciais de
separação d, incluindo o valor d = 12 m e o valor crı́tico
dc , separação máxima para a qual o passageiro ainda
consegue pegar o trem.
(b)
posição (u .a.)
x p (t)
x t (t) com d c
x t (t) com ou tros d 's
(c) Nesta distância dc de separação crı́tica, qual é a velocidade do trem quando o passageiro o alcança?
tem po (u .a.)
(d) Qual a velocidade média do trem no intervalo que vai
de t = 0 até o instante em que o passageiro o alcança?
Qual é o valor dc ?
(c) Existem duas maneiras de resolver. Graficamente é
possı́vel verificar que, nessa situação crı́tica, a inclinação
2
Integrando v(t), obtemos:

3 2

0 ≤ t < 5 s;
 2 t + 10t + k1 ,
25t + k2 ,
5 ≤ t < 10 s;
x(t) =

 10t2 − t3 − 75t + k , 10 ≤ t < 15 s.
3
3
de xt (t) e xp (t) são iguais em t = τc . Logo, neste instante
de tempo, a velocidade do trem é igual à velocidade do
passageiro: vt (τc ) = vm = 3, 1 m/s. Alternativamente,
poderı́amos calcular o instante τc . Para isso, impõe-se
que só exista uma solução para τ (veja o item (a)), ou
seja, queremos que
r
r
2
2
vm
dc
vm
vm
dc
vm
− 2 = 0 =⇒ τc =
±
−2 =
.
2
2
a
a
a
a
a
a
Ainda precisamos encontrar os valores para as constantes
k1 , k2 e k3 . Do enunciado, sabemos que x(0) = 0. Usando esta informação na equação para x(t) que descreve
a primeira parte do movimento:
Logo, sabendo que vt (t) = at, temos que vt (τc ) =
a(vm /a) = vm = 3, 1 m/s.
x(0) = 0 =
(d) Primeiro, calculemos dc :
r
2
vm
dc
−2 =0
a2
a
2
1 vm
1 (3, 1 m/s)2
=⇒ dc =
=
≈ 15, 5m.
2 a
2 (0, 31 m/s2 )
5 2
0 + k1 =⇒ k1 = 0.
2
Analisando ainda a primeira equação para x(t), verificamos que quando t → 5 s temos
x(t → 5) =
x (t )−x (t )
3 2
7
5 + 10 × 5 = 25.
2
2
Essa informação deve estar de acordo com o cálculo da
segunda expressão para x(t), em t = 5 s:
A velocidade média do trem vale vm,t = t ftf −tit i .
Assumindo que estamos analisando a situação crı́tica,
h
i 1
vm 2
1
a
− 2 a × 02
2
a
xt (tf ) − xt (ti )
vm,t =
=
tf − ti
(vm /a)
vm
=
= 1, 55m/s.
2
x(5) = 25 × 5 + k2 =
7
3
25 =⇒ k2 = − 25.
2
2
Agora vamos verificar o valor de x(t → 10), usando a
equação para x(t) que descreve o movimento na segunda
parte. Obtemos
5. O gráfico da figura refere-se ao movimento retilı́neo de
uma partı́cula ao longo do eixo x, partindo da origem.
Entre 10 e 16 s, a expressão para a velocidade da
partı́cula é escrita como v(t) = −t2 + 20t − 75 (SI). De
acordo com este gráfico, responda as questões a seguir.
3
17
x(t → 10) = 25 × 10 + − 25 =
25.
2
2
Essa informação deve estar de acordo com o cálculo da
terceira expressão para x(t), em t = 10 s:
(a) Escreva uma expressão matemática para v(t), x(t) e
a(t) (dica: considere separadamente cada uma das três
partes do movimento).
x(10) = 103 −
(b) Qual a distância percorrida pela partı́cula durante os
primeiros 16, 0 s?
17
103
− 75 × 10 + k3 =
25
3
2
71
=⇒ k3 =
25.
6
(b) A distância percorrida entre t = 0 s e t = 15 s é igual
ao deslocamento neste intervalo de tempo, já que o corpo
não inverte o sentido do movimento. Portanto,
∆x
= x(16) − x(0)
1
71
= 10 × (16)2 − (16)3 − 75 × 16 + 25
3
6
≈ 290, 5 m.
6. O gráfico da figura abaixo refere-se ao movimento
retilı́neo de uma partı́cula ao longo do eixo x, partindo
da origem. De acordo com este gráfico:
(a) Escreva uma expressão matemática para v(t) (dica:
considere separadamente cada uma das três partes do
movimento).
Resolução
(a) Da leitura do gráfico, obtemos:

0 ≤ t < 5 s;
 10 + 3t,
v(t) =
25,
5 ≤ t < 10 s;

2
−t + 20t − 75, 10 ≤ t < 15 s.
Derivando esta expressão, obtemos:

0 ≤ t < 5 s;
 3,
a(t) =
0,
5 ≤ t < 10 s;

−2t + 20, 10 ≤ t < 15 s.
(b) A partir de v(t), escreva uma expressão para x(t) e
outra para a(t) (dica: continue considerando separadamente cada uma das três partes do movimento).
(c) Qual a distância percorrida pela partı́cula durante os
primeiros 15, 0 s?
(d) Esboce o gráfico de x(t), para t = 0 até t = 15, 0 s.
Resolução
3
50
x (m)
parábola (concavidade para baixo)
reta
parábola (concavidade para cima)
0
5
0
7. O gráfico da figura seguinte refere-se ao movimento
retilı́neo de uma partı́cula ao longo do eixo x, partindo
da origem. De acordo com este gráfico:
(a) A expressão matemática para v(t) pode ser lida diretamente no gráfico e vale (unidades no SI):

 t
v(t) =
5

15 − t
(t ≤ 5 s)
(5 s < t ≤ 10 s) .
(10 s < t ≤ 15 s)
(a) Escreva uma expressão matemática para v(t) (dica:
considere separadamente cada uma das três partes do
movimento).
(b) A função x(t) é aquela cuja derivada resulte na
equação anterior. Portanto, em unidades do SI,

1 2
 k1 + 2 t
x(t) =
k + 5t
 2
k3 + 15t − 12 t2
(b) A partir de v(t), escreva uma expressão para x(t) e
outra para a(t) (dica: continue considerando separadamente cada uma das três partes do movimento).
(t ≤ 5 s)
(5 s < t ≤ 10 s) ,
(10 s < t ≤ 15 s)
(c) Qual a distância percorrida pela partı́cula durante os
primeiros 15, 0 s?
(d) Esboce o gráfico de x(t), para t = 0 até t = 15, 0 s.
sendo que k1 , k2 e k3 são constantes. Como a partı́cula
parte da origem, a constante k1 pode ser obtida da
relação
10,0
1
x(0) = k1 + 02 = 0 =⇒ k1 = 0.
2
v (m /s)
7,5
Portanto, para t ≤ 5 s, temos x(t) = 12 t2 =⇒ x(5) =
12, 5. Usando este resultado e a expressão para x(t) no
intervalo 5 s < t ≤ 10 s, podemos encontrar k2 ,
0,0
0,0
2,5
5,0
7,5
10,0
12,5
15,0
t (s)
Portanto, para 5 s < t ≤ 10 s, temos x(t) = −12, 5 +
5t =⇒ x(10) = 37, 5. Usando este resultado e a expressão
para x(t) no intervalo 10 s < t ≤ 15 s, podemos encontrar
k3 ,
Resolução
(a) A expressão matemática para v(t) pode ser lida diretamente no gráfico e vale (unidades no SI):

(t ≤ 5 s)
 5−t
v(t) =
0
(5 s < t ≤ 10 s) .

−10 + t (10 s < t ≤ 15 s)
1
× 102 = 37, 5
2
=⇒ k3 = −62, 5.
x(10) = k3 + 15 × 10 −
A expressão para a(t) é obtida quando deriva-se v(t),
(b) A função x(t) é aquela cuja derivada resulte na
equação anterior. Portanto, em unidades do SI,

1 2
(t ≤ 5 s)
 k1 + 5t − 2 t
x(t) =
k
(5 s < t ≤ 10 s) ,
 2
k3 − 10t + 12 t2 (10 s < t ≤ 15 s)

(t ≤ 5 s)
 1
v(t) =
0
(5 s < t ≤ 10 s) .

−1 (10 s < t ≤ 15 s)
(c) A distância percorrida pode ser obtida da área do
gráfico, ou simplesmente fazendo
=
5,0
2,5
x(5) = k2 + 5 × 5 = 12, 5 =⇒ k2 = −12, 5.
∆x =
15
10
t (s)
sendo que k1 , k2 e k3 são constantes. Como a partı́cula
sai da origem, a constante k1 pode ser obtida da relação
x(15) − x(0)
1
−62, 5 + 15 × 15 − × 152 − 0 = 50.
2
1
x(0) = k1 + 5 × 0 − 02 = 0 =⇒ k1 = 0.
2
Portanto, para t ≤ 5 s, temos x(t) = 5t − 12 t2 =⇒ x(5) =
12, 5. Usando este resultado e a expressão para x(t) no
(d) O gráfico x(t) deve ser:
4
(a) Determine os valores de α e β sabendo que a partı́cula
inverte o sentido de seu movimento no instante t = 1 s e
que possui aceleração constante de −4 m/s2 .
intervalo 5 s < t ≤ 10 s, podemos encontrar k2 ,
x(5) = k2 = 12, 5 =⇒ k2 = 12, 5.
(b) Entre os instantes t = 0 e t = 3 s, esboce o gráfico
de x contra t.
Portanto, para 5 s < t ≤ 10 s, temos x(t) = 12, 5 =⇒
x(10) = 12, 5. Usando este resultado e a expressão para
x(t) no intervalo 10 s < t ≤ 15 s, podemos encontrar k3 ,
x(10) = k3 − 10 × 10 +
(c) Para o mesmo intervalo, determine a distância percorrida e a velocidade média.
1
× 102 = 12, 5
2
=⇒ k3 = 62, 5.
11. A posição de uma partı́cula que se move em linha reta é
dada em função do tempo pela fórmula x(t) = 10−α t2 +
1 4
2 t , na qual o tempo é dado em segundos e a posição
em metros.
A expressão para a(t) é obtida quando deriva-se v(t),

 −1 (t ≤ 5 s)
v(t) =
0
(5 s < t ≤ 10 s) .

1
(10 s < t ≤ 15 s)
(a) Qual a unidade dimensional da constante α?
(b) Determine o valor de α considerando que a partı́cula
inverte o sentido de seu movimento no instante t = 1, 0
s.
(c) A distância percorrida pode ser obtida da área do
gráfico, ou simplesmente fazendo
∆x
(c) Calcule a velocidade média da partı́cula entre os instantes t = 1, 0 s e t = 3, 0 s.
= x(15) − x(0)
1
=
62, 5 − 10 × 15 + × 152 − 0 = 25.
2
(d) Esboce o gráfico da aceleração da partı́cula em função
do tempo durante os três primeiros segundos do movimento.
(d) O gráfico x(t) deve ser:
12. Um próton se move ao longo do eixo x segundo a equação
x = 50 t + 10 t2 , onde x está em metros e t está em
segundos.
50
x (m)
parábola (concavidade para cima)
(a) Calcule a velocidade média do próton durante os
primeiros 3, 0 s do seu movimento.
reta
(b) Calcule a velocidade instantânea do próton em t =
3, 0 s.
(c) Calcule a aceleração instantânea do próton em t =
3, 0 s.
parábola (concavidade para baixo)
0
0
5
t (s)
10
15
(d) Trace o gráfico de x contra t e mostre como a resposta
para (a) pode ser obtida através do gráfico.
8. A posição de uma partı́cula que se move em linha reta é
dada em função do tempo pela fórmula x(t) = a+b t+c t2 ,
na qual o tempo é dado em segundos e a posição em
metros. a, b e c são constantes.
13. Uma pára-quedista salta de pára-quedas e cai 50 m livremente. Então o pára-quedas se abre, e daı́ em diante ela
desacelera a 2, 0 m/s2 . Ela atinge o chão com uma velocidade de 3, 0 m/s.
(a) Determine os valores de a, b e c a partir das seguintes
considerações: (1) a partı́cula passa pela origem do sistema de coordenadas em t = 0, (2) inverte o sentido de
seu movimento no instante t = 1 s e (3) possui aceleração
constante de −4 m/s2 .
(a) Quanto tempo a pára-quedista fica no ar?
(b) A que altura começa a queda?
14. Uma bola de futebol é chutada do chão com uma velocidade inicial de 70, 2 km/h fazendo um ângulo de 45, 0o
para cima. Naquele instante, o goleiro a uma distância
de 52, 8 m na direção do chute começa a correr para receber a bola e consegue chegar a tempo de agarrá-la no
ar (sem saltar) a uma altura de 2, 45 m simplesmente
erguendo os braços.
(b) Entre os instantes t = 0 e t = 3 s, esboce o gráfico
da posição da partı́cula em função do tempo.
(c) Para o mesmo intervalo do item anterior, determine
a distância percorrida e o deslocamento.
9. Defina, sem utilizar fórmulas, as grandezas fı́sicas
aceleração média e aceleração instantânea, enfatizando
as diferenças entre elas.
(a) Qual foi o tempo de vôo da bola?
(b) Qual foi a velocidade escalar média desenvolvida pelo
goleiro?
Resolução
10. A posição de uma partı́cula que se move em linha reta é
dada em função do tempo pela fórmula x(t) = α2 t + β t2 ,
na qual o tempo é dado em segundos e a posição em
metros. α e β são constantes.
(a) Considerando que, no momento do chute, a bola esteja na origem do eixo de coordenadas, a expressão geral
5
(c) Desenhe, na trajetória esboçada, o vetor velocidade
para t = 0 s e t = 1/4 s.
para o movimento do projétil é dada por:
~r(t) = (v0x t)ı̂ + (v0y t − 12 gt2 )̂,
~v (t) = v0x ı̂ + (v0y − gt)̂,
~a(t) = −g̂,
(d) Determine o vetor aceleração em função do tempo.
Qual é a sua direção?
Resolução
sendo
v0x
|~v0 | cos 45◦ = (70, 2 km/h) cos 45◦
√
2
≈ (13, 8 m/s),
(19, 5 m/s)
2
◦
|~v0 | sin 45 ≈ (13, 8 m/s).
=
=
v0y
(a) Usando ~r(t) = 2 sen(2πt) ı̂ + 2 cos(2πt) ̂, podemos
substituir alguns valores de t para ter uma idéia do que
seria o movimento (em unidades SI):
=
~r(t = 0) = 0 ı̂ + 2 ̂,
√
√
~r(t = 3/8) = 2 ı̂ − 2 ̂,
~r(t = 3/4) = −2 ı̂ + 0 ̂,
Supondo que a bola atingiu a altura yG = 2, 45 m no
instante τ , podemos escrever
~r(t = 1/4) = 2 ı̂ + 0 ̂,
√
√
~r(t = 5/8) = − 2 ı̂ − 2 ̂,
~r(t = 1) = 0 ı̂ + 2 ̂.
~r(τ ) = L ı̂ + yG ̂,
Este cálculo sugere que a trajetória é circular de raio
2 m, com a partı́cula se movimentando no sentido horário
– incluindo o esboço da trajetória). Porém, podemos
confirmar a expectativa de que a trajetória é circular
calculando |~r(t)|:
p
|~r(t)| =
[2 sen(2πt)]2 + [2 cos(2πt)]2
p
=
4[sen2 (2πt) + cos2 (2πt)] = 2.
sendo L a coordenada x da bola neste instante τ . Por
outro lado, da equação de movimento,
1
~r(τ ) = (v0x τ )ı̂ + (v0y τ − gτ 2 )̂ = Rı̂ + yG ̂.
2
Igualando as componentes y:
1
2v0y
2yG
v0y τ − gτ 2 = yG =⇒ τ 2 −
τ+
=0
2
g
g
s
2
4v0y
v0y
8yG
=⇒ τ =
±
−
.
2
g
g
g
Através desta expressão mostramos que, para qualquer
instante de tempo t, a distância da partı́cula à origem é
sempre 2 m, e, portanto, a trajetória é circular.
(b) Obtemos o vetor velocidade através da operação:
Substituindo os valores:
s
2
4v0y
v0y
8yG
τ =
±
−
2
g
g
g
i
h
p
≈ 1, 38 ± 4(1, 38)2 − 8(0, 245) s
~v (t) =
~v (1/4) = 4π cos(2π × 1/4) ı̂ − 4π sen(2π × 1/4) ̂ = −4π ̂.
O restante dos pontos será atribuı́do ao desenho do vetor
velocidade na trajetória.
(b) Do enunciado, podemos dizer que a posição inicial do
(G)
goleiro é xi = 52, 8 m. Quando ele agarrou a bola, sua
(G)
coordenada x era xf = L, sendo que R é dado por
(d) Obtemos o vetor aceleração através da operação:
~a(t)
v0x τ = L
=⇒ L = (13, 8 m/s) × (2, 57 s) = 35, 5 m.
=
(G)
− xi
τ −0
=
d
d
~v (t) =
[4π cos(2πt) ı̂ − 4π sen(2πt) ̂]
dt
dt
= −8π 2 sen(2πt) ı̂ − 8π 2 cos(2πt) ̂.
=
O vetor aceleração está sempre “apontando” para o centro da trajetória. Existe uma maneira de provar isso,
mostrando que |~a(t) · ~r(t)| = |~r(t)||~a(t)|.
Portanto, como a distância percorrida pelo goleiro é igual
ao seu deslocamento
(G)
d
[2 sen(2πt) ı̂ + 2 cos(2πt) ̂]
dt
= 4π cos(2πt) ı̂ − 4π sen(2πt) ̂.
=
~v (0) = 4π cos(2π × 0) ı̂ − 4π sen(2π × 0) ̂ = 4π ı̂,
O valor menor de τ refere-se ao instante em que a bola
passou pela posição yG , subindo. Procuramos o instante
em que a bola está em yG , só que descendo: τ = 2, 57 s.
xf
d
~r(t)
dt
(c) Usando o cálculo anterior:
= 1, 38 ± 1, 19.
s(G)
m
√
√
~r(t = 1/8) = 2 ı̂ + 2 ̂,
~r(t = 1/2) = 0 ı̂ − 2 ̂,
√
√
~r(t = 7/8) = − 2 ı̂ + 2 ̂, .
17, 3 m
= 6, 73 m/s.
2, 57 s
16. Uma bola é lançada no plano inclinado da figura abaixo,
tocando o solo 1, 5 s após deixá-lo.
(a) Qual é a velocidade vetorial da bola ao deixar o
plano?
15. A posição de uma partı́cula em função do tempo é dada
por: r(t) = 2 sen(2πt) i + 2 cos(2πt) j, sendo que r é
dado em metros e t em segundos.
(b) Qual é a altura máxima atingida pela bola, medida
em relação à base do plano?
(a) Qual é a trajetória da partı́cula? Esboce-a no plano
(x, y).
(c) Qual é o ponto em que a bola toca o solo?
(b) Determine o vetor velocidade em função do tempo.
(d) Qual é a velocidade vetorial neste ponto?
6
(e) Nesta situação, a única alteração seria que v0x =
(22/3 m/s) + (5 m/s) = 37/3 m/s. Logo, no item (c),
R = v0x τ = (37/3 m/s) × (1, 5 s) = 18, 5 m.
17. Dois segundos após ter sido arremessado do nı́vel do chão,
um projétil se deslocou L = 40 m na horizontal e h =
53 m na vertical.
(a) Escreva, num sistema de coordenadas conveniente, as
expressões para ~r(t), ~v (t) e ~a(t) para esse problema.
(b) Quais são as componentes vertical e horizontal da
velocidade inicial do projétil?
(c) No instante em que o projétil alcança a sua altura
máxima acima do nı́vel do solo, qual é a distância percorrida na horizontal a partir do ponto de lançamento?
Resolução
(e) Se o plano inclinado estivesse se movendo com velocidade v = 5 m/s na direção do eixo x, qual seria a
resposta do item (c)?
Resolução
(a) Considerando que o canhão se encontra na origem do
sistema de coordenadas,
(a) Podemos descrever o movimento do projétil através
das equações:
1
~r(t) = (v0x t)ı̂ + ho + v0y t − gt2 ̂,
2
~v (t) = (v0x )ı̂ + (v0y − gt) ̂,
~r(t) = (v0x t)ı̂ + (v0y t − 12 gt2 )̂,
~v (t) = v0x ı̂ + (v0y − gt)̂,
~a(t) = −g̂.
~a(t) = (−g) ̂.
(b) Segundo o enunciado,
2
g ~r(2) = (2v0x )ı̂ + 2v0y − 22 ̂ = Lı̂ + h̂.
2
v0x = L/2 = 20 m/s
=⇒
.
v0y = (h + 2g)/2 = 36, 5 m/s
Sabemos, nesta expressão, que h0 = 3 m e g = 10 m/s .
Do enunciado, sabemos que, no instante t = τ = 1, 5 s
(chamando o alcance de R),
1 2
~r(τ ) = R ı̂ + 0 ̂ = (v0x τ )ı̂ + ho + v0y τ − gτ ̂
2
v0x τ = R
=⇒
.
ho + v0y τ − 12 gτ 2 = 0
(c) No instante tM em que atinge a altura máxima, sabemos que vy (tM ) = v0y − gtM = 0. Logo, tM = v0y /g =
3, 6 s. Para saber o deslocamento horizontal, basta fazer
x(tM ) = v0x tM = 72 m.
Resolvendo a segunda equação,
v0y =
1
h0
1
3m
gτ −
= (10 m/s2 ) × (1, 5 s) −
= 5, 5 m/s.18. Uma bola é atirada do chão no ar. Em uma altura h =
2
τ
2
1, 5 m/s
9, 1 m, num instante τ , observa-se que sua velocidade é
v
0y
= 34 . Portanto,
Da figura do enunciado sabemos que v0x
4
v0x = 3 v0y = 22/3 m/s e ~v (0) = (22/3) ı̂ + 5, 5 ̂ (em
m/s).
de ~v (τ ) = vx (τ ) ı̂ + vy (τ ) ̂ = 7, 6 ı̂ + 6, 1 ̂, em metros
por segundo (ı̂ horizontal, ̂ para cima).
(a) Escreva, num sistema de coordenadas conveniente, as
expressões para ~r(t), ~v (t) e ~a(t) para esse problema.
(b) A bola atingirá sua altura máxima hm no instante
de tempo tm tal que a componente y de sua velocidade
seja nula, vy (tm ) = v0y − gtm = 0. Resolvendo esta
equação, tm = v0y /g = 0, 55 s. A altura máxima hm
será a coordenada y da bola neste instante de tempo,
hm
=
=
=
(b) Até que altura máxima a bola sobe?
(c) Qual a distância horizontal total que a bola percorre
até voltar ao chão?
(d) Qual é a velocidade (vetor) da bola imediatamente
antes dela bater no chão?
Resolução
1
h0 + v0y tm − gt2m
2
2
2
v0y
1 v0y
h0 +
−
g
2 g
2
1 v0y
1 (5, 5 m/s)2
h0 +
= 3 m+
≈ 4, 51 m.
2 g
2 (10 m/s2 )
(a) Considerando que a bola se encontra na origem do
sistema de coordenadas no instante inicial,
~r(t) = (v0x t)ı̂ + (v0y t − 12 gt2 )̂,
~v (t) = v0x ı̂ + (v0y − gt)̂,
~a(t) = −g̂.
(c) O ponto em que a bola toca o solo (alcance R) é a
sua coordenada x no instante t = τ = 1, 5 s:
v0x τ = R
=⇒
R = (22/3 m/s) × (1, 5 s) = 11 m.
Segundo o enunciado, sabemos os valores ~v (τ ) = vx (τ ) ı̂+
vy (τ ) ̂ e y(τ ) = h. Por outro lado, das equações anteriores,
(d) A velocidade neste instante vale
~v (τ ) = (v0x ) ı̂ + (v0y − gτ ) ̂
= (22/3 m/s) ı̂ + (5, 5 m/s) − (10 m/s2 ) × (1, 5 s) ̂
= (22/3 m/s) ı̂ + (−9, 5 m/s) ̂.
7
~v (τ ) = (v0x )ı̂ + (v0y − gτ ) ̂,
1
~r(τ ) = (v0x τ )ı̂ + (v0y τ − gτ 2 )̂.
2
(b) Segundo o enunciado |~v0 | = 82 m/s. Para que a bala
atinja o navio, deve existir um instante de tc tal que
g
~r(tc ) = (v0x × tc )ı̂ + v0y × tc − × t2c ̂ = Lı̂ + 0̂.
2
v0x tc = tc |~v0 | cos θ0 = L
=⇒
.
c
c
tc v0y − g×t
= tc |v0 | sin θ0 − g×t
=0
2
2
Juntando as duas informações: v0x = vx (τ ) = 7, 6 m/s e:
v0y − gτ = vy (τ )
v0y τ − gτ 2 = τ vy (τ )
=⇒
.
1
2
v0y τ − 12 gτ 2 = h
v0y τ − 2 gτ = h
Subtraindo uma equação da outra, achamos o valor de τ ,
#
"
s
vy (τ )
2hg
τ =−
1∓ 1+
2 .
g
vy (τ )
Isolando tc na primeira equação e substituindo na segunda,
gL
2|v0 | sin θ0 =
|~v0 | cos θ0
gL
=⇒ 2 sin θ0 cos θ0 = sin(2θ0 ) =
|~v0 |2
10 m/s2 × 560 m
= 0, 83
=⇒ sin(2θ0 ) =
(82 m/s)2
=⇒ 2θ0 = 56◦ ou 2θ0 = 124◦ .
Como vy (τ ) = 6, 1 m/s é positiva, devemos escolher o
sinal negativo na equação anterior. Assim:
"
#
s
vy (τ )
2hg
τ = −
1− 1+
2
g
vy (τ )
r
6, 1
2 × 9, 1 × 10
= −
1− 1+
≈ 0, 87 s.
10
6, 12
Obtemos, portanto:
v0y = vy (τ ) + gτ = [6, 1 + 10 × 0, 87] m/s ≈ 15 m/s.
Logo, o canhão poderia disparar com uma inclinação θ0
de 28◦ ou 62◦ .
Assim as equações para o movimento do projétil ficam
completamente determinadas.
(c) Podemos inverter umas das fórmulas escritas anteriormente e escrever a distância L em função de θ0 ,
(b) No instante tM em que atinge a altura máxima, sabemos que vy (tM ) = v0y − gtM = 0. Logo, tM = v0y /g =
1, 5 s. Para saber o deslocamento vertical, que é, neste
caso, equivalente à altura máxima atingida, basta calcular
L=
O lado direito desta expressão vale, no máximo, |~v0 |2 /g =
672 m. Logo, se L for maior que esta distância, torna-se
impossı́vel resolver esta equação (não existiria o instante
tc que resolveria o problema proposto).
1
y(tM ) = v0y tM − gt2M = 11 m.
2
(c) No instante tf em que a bola volta ao chão, sabemos
que y(tf ) = v0y tf − 12 gt2f = 0. Logo, tf = 2v0y /g ≈
3 s. Para saber o deslocamento horizontal nesta situação,
basta calcular
20. Um avião, que mergulha fazendo um ângulo de 53, 0◦
com a vertical, solta um projétil de uma altitude de 730
m. O projétil bate no chão 5, 00 s após ser solto.
(a) Qual é a velocidade da aeronave?
x(tf ) = v0x tf ≈ (7, 6 × 3) ≈ 22 m.
(b) Que distância o projétil percorreu na horizontal durante o seu vôo?
A velocidade, neste instante tf , vale (em m/s):
~v (tf ) =
≈
|~v0 |2 sin(2θ0 )
.
g
21. Dois prédios paralelos estão separados por uma avenida,
de modo que a distância entre suas paredes é de 15,0 m.
Uma criança atira uma bola de tênis pela janela de seu
apartamento. A bola sai horizontalmente pela janela a
uma altura de 78,4 m (em relação à avenida) com velocidade de módulo 5,00 m/s. Despreze a resistência do
ar.
v0x ı̂ + (v0y − gtf )̂
7, 6ı̂ + (15 − 10 × 3)̂ = 7, 6ı̂ − 15̂.
19. Um navio pirata está a uma distância L = 560 m de um
forte que protege a entrada do porto de uma ilha. Um
canhão de defesa, situado ao nı́vel do mar, dispara balas
com uma velocidade inicial igual a |~v0 | = 82 m/s.
(a) Escreva, num sistema de coordenadas conveniente, as
expressões para ~r(t), ~v (t) e ~a(t) para esse problema.
(a) Sabendo que a bola colide com o prédio da frente
antes de cair na avenida, calcule a altura em que ocorre
a colisão?
(b) Com que ângulo θ0 , medido a partir da horizontal,
deve-se disparar uma bala pra que ela alcance o navio?
(b) A que distância do prédio com o qual colidiu, a bola
cai na avenida?
(c) A que distância o navio pirata deveria estar do canhão
para que esteja fora do alcance de suas balas?
Resolução
(c) Se a bola saı́sse do prédio fazendo um ângulo de 45,0◦
para cima da horizontal, que valor mı́nimo para o módulo
da velocidade inicial da bola garantiria pelo menos uma
colisão com o prédio da frente antes da queda da bola na
avenida?
(a) Considerando que o canhão se encontra na origem do
sistema de coordenadas,
~r(t) = (v0x t)ı̂ + (v0y t − 12 gt2 )̂,
~v (t) = v0x ı̂ + (v0y − gt)̂,
~a(t) = −g̂.
22. Uma carabina é apontada na horizontal para um alvo
distante 30 m. A bala acerta o alvo 1, 9 cm abaixo do
ponto visado.
8
(a) Qual é o tempo de vôo da bala?
parada, a pessoa sobre em ∆t1 = 90 s:
(b) Qual é o módulo da sua velocidade ao sair da carabina?
vP E =
23. Um projétil é lançado com velocidade escalar inicial v0
numa direção que forma um ângulo θ0 com a horizontal. Mostre que a altura máxima que o prójetil alcança
é ymax = (v0 senθ0 )2 /2g.
Portanto, calculamos vP O :
vP O = vP E + vEO =
D
D
+
.
∆t1
∆t2
Logo, o intervalo de tempo foi de:
24. Um barco está viajando rio acima a vBA = 14 km/h
em relação à água deste rio. A água está escoando a
vAM = 9 km/h em relação às margens.
∆t
=
=
(a) Qual é a velocidade do barco em relação às margens?
Explique cuidadosamente.
D
∆t1 ∆t2
=
vP O
∆t1 + ∆t2
5400
s = 36 s.
150
(b) Da última expressão, construı́da literalmente, sem
substituir valores, verificamos que o tempo gasto para
subir a escada só depende explicitamente de ∆t1 e ∆t2 .
Portanto, a resposta não depende explicitamente de D,
o tamanho da escada.
(b) Uma criança no barco caminha da frente para a parte
de trás a 6 km/h em relação ao barco. Qual é a velocidade desta criança em relação às margens? Explique
cuidadosamente.
Resolução
26. Uma pessoa parada observa um trem viajando a uma
velocidade |~vT P | = 30 m/s para a direita. Ao mesmo
tempo, cai uma chuva. Devido ao vento, esta pessoa
observa as gotas da chuva cairem com uma velocidade
constante e inclinação θ = 60◦ em relação à vertical,
também para a direita.
(a) Para um observador situado nas margens, supomos
que o barco viaja no sentido positivo de x. A água, portanto, corre no sentido negativo. Logo, em unidades do
SI, ~vBA = 14ı̂ e ~vAM = −9ı̂. Sabemos que a velocidade
~vBM do barco em relação às margens se relaciona com
~vAM e ~vBA da seguinte maneira ~vBM = ~vBA + ~vAM .
Logo, ~vBM = 14ı̂ − 9ı̂ = 5ı̂ (em km/h).
(a) Adote um sistema de coordenadas conveniente e,
usando versores, escreva a velocidade ~vT P do trem em
relação à pessoa e a velocidade ~vGP das gotas também
em relação à pessoa.
(b) A velocidade ~vCB = −(6 km/h)ı̂ da criança em
relação ao barco se relaciona com ~vBM = (5 km/h)ı̂ (velocidade do barco em relação às margens) e ~vCM (velocidade da criança em relação às margens) da seguinte
maneira ~vCM = ~vCB +~vBM . Logo, ~vCM = −(6 km/h)ı̂+
(5 km/h)ı̂ = −(1 km/h)ı̂.
(b) Uma outra pessoa dentro do trem, no mesmo instante, vê as gotas caı́rem com velocidade ~vGT exatamente na direção vertical. Determine o módulo da velocidade ~vGP das gotas em relação ao observador de fora
do trem.
Resolução
25. Uma pessoa sobe caminhando em 90 s uma escada
rolante enguiçada que possui 15 m de comprimento.
Quando parada em relação à mesma escada rolante,
agora em movimento, a pessoa é transportada para cima
em 60 s.
y 6
x
(a) Para o observador parado, supomos um eixo de coordenadas conforme desenhado acima, e imediatamente
escrevemos
(a) Quanto tempo essa pessoa levaria para subir caminhando na escada rolante em movimento?
(b) A resposta depende do comprimento da escadarolante?
Resolução
~vT P = |~vT P |ı̂ = 30ı (em m/s),
~vGP = |~vGP | sin 60◦ ı̂ − |~vGP | cos 60◦ ̂.
(a) Para saber este intervalo de tempo, precisamos calcular a velocidade vP O da pessoa P , na situação em que
a escada também se move, para um referencial O fixo ao
solo.
(b) Para um passageiro dentro do trem, ~vGT = −|~vGT |̂.
A velocidade ~vGP das gotas em relação ao observador
de fora do trem se relaciona com ~vT P e ~vGT da seguinte
maneira:
Pelo enunciado, podemos calcular a velocidade vEO da
escada E em relação a O, já que a pessoa, parada em
relação à escada, sobe em ∆t2 = 60 s:
vEO =
D
.
∆t1
~vGP = ~vGT + ~vT P .
Logo,
D
,
∆t2
|~vGP | sin 60◦ ı̂ − |~vGP | cos 60◦ ̂ = −|~vGT |̂ + |~vT P |ı̂
=⇒ |~vGP | sin 60◦ = |~vT P | e
sendo D = 15 m o tamanho da escada.
Portanto,
da √
primeira
|~vT P |/ sin 60◦ = 20 3 m/s.
Por outro lado podemos calcular a velocidade vP E da
pessoa P com relação a escada, já que, se a escada fica
9
|~vGP | cos 60◦ = |~vGT |.
igualdade,
|~vGP |
=
27. Um avião se move para o leste enquanto o piloto aproa
o avião um pouco para o sul a partir do leste, contra
um vento regular que sopra pra nordeste. O avião possui
velocidade ~vAV em relação ao vento de 215 km/h, na
direção sudeste fazendo um ângulo θ com o leste. O vento
possui velocidade ~vV C em relação ao chão, de módulo
65 km/h, na direção nordeste fazendo um ângulo de 30◦
com o norte.
(a)Qual é o módulo da velocidade ~vAC do avião em
relação ao chão?
(b) Qual é o valor de θ?
Resolução
Em primeiro lugar, vamos assumir que o eixo x aponta
de oeste para leste, e o eixo y de sul para norte. Com
relação ao chão, a velocidade do avião pode ser escrita
como
~vAC = |~vAC | ı̂.
Com relação à velocidade do avião com relação ao vento,
podemos afirmar que:
~vAV = |~vAV | cos θı̂ − |~vAV | sin θ̂,
com |~vAV | = 215 km/h. E a velocidade do vento com
relação ao chão vale:
~vV C = |~vV C | sin 30◦ ı̂ + |~vV C | cos 30◦ ̂,
com |~vAV | = 215 km/h. Estas três velocidades se relacionam da seguinte maneira:
~vAC
= ~vAV + ~vV C
=
+
(|~vAV | cos θ + |~vV C | sin 30◦ ) ı̂
(−|~vAV | sin θ + |~vV C | cos 30◦ ) ̂.
Comparando a última equação com a primeira, notamos
que a coordenada y da última deve se anular:
−|~vAV | sin θ + |~vV C | cos 30◦ = 0
|~vV C |
cos 30◦ ≈ 0, 26 =⇒ θ ≈ 15◦ .
=⇒ sin θ =
|~vAV |
Usando este valor na componente x,
~vAC
≈ (|~vAV | cos 15◦ + |~vV C | sin 30◦ ) ı̂
≈ (241 km/h) ı̂.
10