Resolução do 1o Teste de Biofísica

Resolução do 1o Teste de Biofísica
11 de Novembro de 2008
Ano lectivo: 2008/2009, semestre ímpar
Docente: Prof. Alfred Stadler
Duração: 2 horas
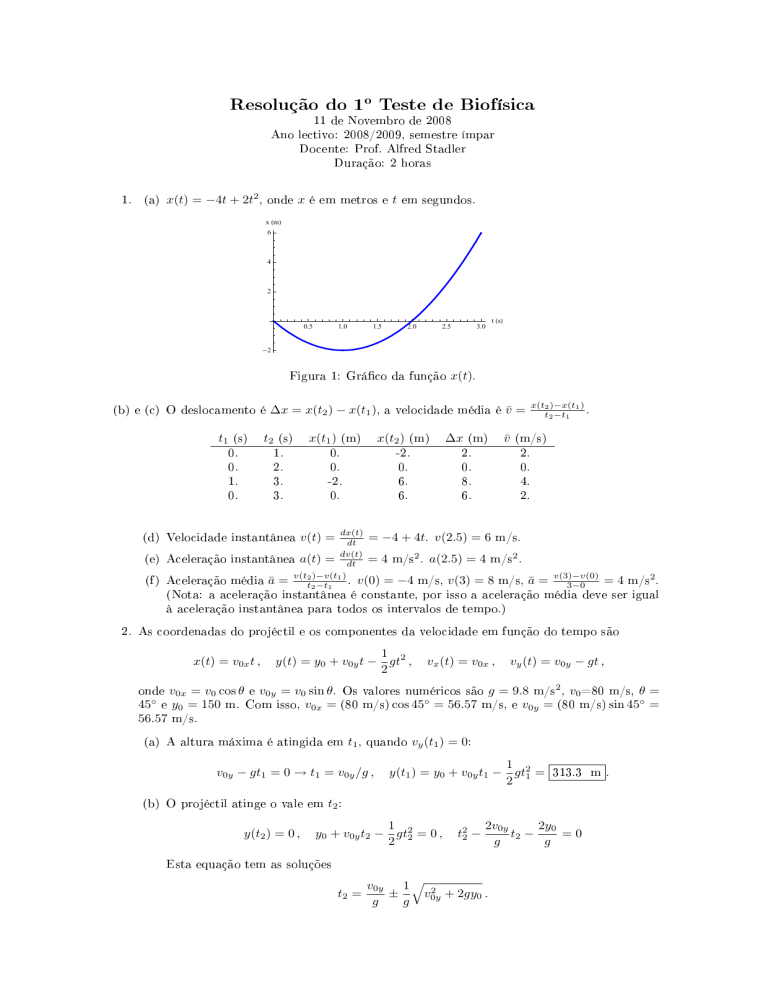
1. (a) x(t) = −4t + 2t2 , onde x é em metros e t em segundos.
x HmL
6
4
2
0.5
1.0
1.5
2.0
2.5
3.0
t HsL
-2
Figura 1: Gráco da função x(t).
(b) e (c) O deslocamento é ∆x = x(t2 ) − x(t1 ), a velocidade média é v̄ =
t1 (s)
0.
0.
1.
0.
t2 (s)
1.
2.
3.
3.
x(t1 ) (m)
0.
0.
-2.
0.
x(t2 ) (m)
-2.
0.
6.
6.
∆x (m)
2.
0.
8.
6.
x(t2 )−x(t1 )
.
t2 −t1
v̄ (m/s)
2.
0.
4.
2.
dx(t)
dt = −4 + 4t. v(2.5) = 6 m/s.
2
2
instantânea a(t) = dv(t)
dt = 4 m/s . a(2.5) = 4 m/s .
1)
média ā = v(t2t2)−v(t
. v(0) = −4 m/s, v(3) = 8 m/s,
−t1
(d) Velocidade instantânea v(t) =
(e) Aceleração
(f) Aceleração
ā = v(3)−v(0)
= 4 m/s2 .
3−0
(Nota: a aceleração instantânea é constante, por isso a aceleração média deve ser igual
à aceleração instantânea para todos os intervalos de tempo.)
2. As coordenadas do projéctil e os componentes da velocidade em função do tempo são
x(t) = v0x t ,
1
y(t) = y0 + v0y t − gt2 ,
2
vx (t) = v0x ,
vy (t) = v0y − gt ,
onde v0x = v0 cos θ e v0y = v0 sin θ. Os valores numéricos são g = 9.8 m/s2 , v0 =80 m/s, θ =
45◦ e y0 = 150 m. Com isso, v0x = (80 m/s) cos 45◦ = 56.57 m/s, e v0y = (80 m/s) sin 45◦ =
56.57 m/s.
(a) A altura máxima é atingida em t1 , quando vy (t1 ) = 0:
v0y − gt1 = 0 → t1 = v0y /g ,
1
y(t1 ) = y0 + v0y t1 − gt21 = 313.3 m .
2
(b) O projéctil atinge o vale em t2 :
y(t2 ) = 0 ,
1
y0 + v0y t2 − gt22 = 0 ,
2
t22 −
2v0y
2y0
t2 −
=0
g
g
Esta equação tem as soluções
t2 =
1q 2
v0y
±
v0y + 2gy0 .
g
g
Apenas a solução com o sinal + é relevante, porque a outra corresponde a t2 < 0.
Portanto,
v0y
1q 2
t2 =
+
v0y + 2gy0 , → x(t2 ) = v0x t2 = 778.8 m .
g
g
3. (a) A força gravítica sobre o bloco pode ser decomposta em componentes paralelas e perpendiculares ao plano inclinado: F~G = F~k + F~⊥ , com os módulos Fk = FG sin θ,
~ = −F~⊥ .
F⊥ = FG cos θ, e FG = mg . A força normal ao plano é N
~
N
F~c
F~⊥
θ
θ
F~G
F~k
Fk = mg sin θ = ma
⇒
a = g sin θ .
O tempo para deslizar a distância d =2 m é
d=
1 2
1
at = g sin θt2
2
2
1
⇒
t=
p
2d/g sin θ
e a velocidade após o tempo t é
v = at = g sin θ
p
2d/g sin θ =
p
2dg sin θ .
Substituindo θ = 15◦ , d=2 m, g = 9.8 m/s2 , obtem-se v=3.19 m/s .
(b) O módulo da força do atrito cinético é Fc = µc N = µc mg cos θ. A força total paralela
ao plano (sentido positivo para baixo) é Ftotal = Fk − Fc = mg sin θ − µc mg cos θ =
mg(sin θ − µc cos θ) = ma. Após divisão por m obtem-se a aceleração para baixo, a =
g(sin θ − µc cos θ). Substituir os valores numéricos θ = 15◦ , µc = 0.6 e g = 9.8 m/s2 ,
resulta em a = −3.14 m/s2 . O resultado negativo signica que a força de atrito é mais
forte do que a componente da força gravítica paralela ao plano. Aqui podia-se cair na
armadilha de pensar que o bloco acelera para cima, mas esta conclusão estaria errada. A
interpretação correcta é que devido ao atrito o bloco ca imobilizado, e a sua aceleração
é a = 0.
4. (a) O momento duma força é ~τ = ~r × F~ . Para as três forças indicadas no gráco, F~
e ~r são perpendiculares, e o módulo do momento de força é simplesmente τ = rF .
Assim obtem-se τ1 = (0.25 m)(10 N) = 2.5 Nm, τ2 = (0.25 m)(9 N) = 2.25 Nm, e τ3 =
−(0.1 m)(12 N) = −1.2 Nm, onde um sinal positivo indica que o sentido do momento é
dirigido para dentro do plano das roldanas, e um sinal negativo o sentido para fora.
(b) O módulo do momento total é τ = τ1 + τ2 + τ3 = +3.55 Nm.
2
(c) A aceleração angular é α = τ /I = (3.55 Nm)/(1.5 kg m2 ) = 2.37 rad/s .
(d) O ângulo de rotação das roldanas obtem-se de θ = 21 αt2 = 4.733 rad = 271.2◦ .