Exercício - GEOCITIES.ws

C
C
n
o
d
d
E
d
u
o
T
n
o
ó
g
d
B
h
Ceeen
ntttrrro
o FFFeeed
deeerrraaalll d
deee E
Ed
du
ucccaaaçççããão
oT
Teeecccn
no
ollló
óg
giiicccaaa d
daaa B
Baaah
hiiiaaa.
Disciplina: MAT202 - Matemática – Segundo Ano do Ensino Médio
Professor: Damásio
impressso: 30/05/17, 09:14:01h, arquivo: trigoinversas.doc
Funções Trigonométricas Inversas
Índice
Inversa da função f(x)=senx _____________________________________________ 1
Inversa da função f(x)=cosx _____________________________________________ 2
Inversa da função f(x)=tgx ______________________________________________ 2
Exercícios ____________________________________________________________ 3
Aplicação ____________________________________________________________ 8
Bibliografia __________________________________________________________ 9
Resolução ____________________________________________________________ 9
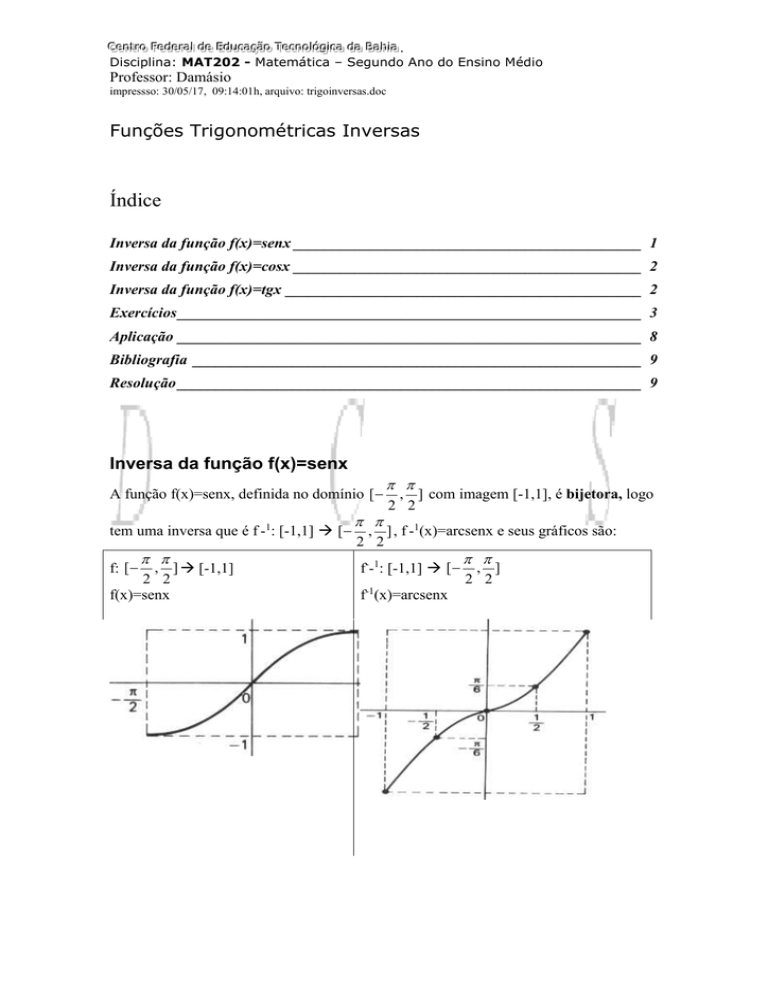
Inversa da função f(x)=senx
A função f(x)=senx, definida no domínio [ 
tem uma inversa que é f -1: [-1,1]  [ 
f: [ 
 
, ]  [-1,1]
2 2
f(x)=senx
 
 
, ] com imagem [-1,1], é bijetora, logo
2 2
, ] , f -1(x)=arcsenx e seus gráficos são:
2 2
f--1: [-1,1]  [ 
f-1(x)=arcsenx
 
, ]
2 2
Funções Trigonométricas Inversas; Arquivo trigoinversas.dcs
—Page 2/9
Inversa da função f(x)=cosx
A função f(x)=cosx, definida no domínio [0,  ] com imagem [-1,1], é bijetora, logo
tem uma inversa que é f -1: [-1,1]  [0,  ] , f -1(x)=arc cosx e seus gráficos são:
f: [0,  ]  [-1,1]
f(x)=cosx
f-1: [1,1]  [0,  ]
f-1(x)=arccosx
Inversa da função f(x)=tgx
A função f(x)=tgx, definida no domínio ] 
uma inversa que é f -1: R ] 
f: ] 
 
, [ R
2 2
f(x)=tgx
 
 
, [ com imagem R, é bijetora, logo tem
2 2
, [ , f-1(x)=arctgx e seus gráficos são:
2 2
f-1: R ] 
 
, [
2 2
f-1(x)=arctgx
Funções Trigonométricas Inversas; Arquivo trigoinversas.dcs
—Page 3/9
Exercícios
1. Escreva na forma trigonométrica inversa:
a) senx = 1 ; Resolvendo: senx  1  x  arcsen 1
2
2
2
b) cosx = 0
c) tgx = 2
2. Determine x nos seguintes casos:
2
a) arc cos
= x; Resolvendo:
2
R. x=arccos 0
R. x=arctg 2
arccos
2
2
2 2
2

 x  cos x 
 e  senx 
x
2
2
4 4
4
4
R.

4
b) arc sen (-1) = x
R. 
c) arc tg (-1) = x
R. 

2

4
3. Calcule:

3

a) y = tg 2.  arcsen

2



 3 
b) y = tg arcsen   
 5 

4. Calcule:
a) cos (2.arccos 1)
b) tg (2.arctg 1)
R.  3
R. 
3
4
R. 1
R. não existe tg

2
Funções Trigonométricas Inversas; Arquivo trigoinversas.dcs


c) arcsen  cos 
3

R.
—Page 4/9

6
5. Calcule o valor de:
a) tg (arc tg 0)

2

b) sen  arccos

4


4

c) cos  arcsen 
5

R. 0
14
4
R.
R.
3
5
6. Calcule y, sendo:
a) y = sen (arc sen 1)
R. 1
b) y = arc sen (sen 0)
R. 0
2 6 1
1
1

c) y = sen  arccos  arcsen 
R.
2
3
6

7. Determine o domínio de cada função:
a) y = arc sen4x;
Resolvendo: o domínio da função arco seno é [-1; 1] 
1  4 x  1
R.
1
1

x  R |   x  
4
4

b) y = arc cos2x
R.
1

x  R | 0  x  
2

c) f(x) = arc sen2x
1 1
R.  , 
8. (Bb47)
 2 2
Determine o domínio de cada função:
a) y  arcsen 2 x  3 
® D=  ; 2
2 
3
 1 x 2 


 2x 
b) y  arcsen
9. (Bb47)
® D={-1; 1}
Resolva as equações
a) arcsenx=arctg2x.
 2 
x 
b) arcsenx=arccos 
 4 
c) arcsen x  arccos x 
10.

2

3
3
,0,
R. S= 

2 
 2
2 2 
R. S= 

 3 
® 0  x 1
(Bb01, page 206, questão 386a, 376a) Calcule:
a) y = arc tg
1
1
+ arc tg
2
3
R.

4
Funções Trigonométricas Inversas; Arquivo trigoinversas.dcs
3
5

b) tg arcsen  arctg 
5
12 

—Page 5/9
® 16/63
11. (Bb01, page 212, questão 387)
2
12 

Prove as igualdades:
12. (Bb01, page 212, questão 388)
Resolva a equação:
a ) 2.arctg  arccos 

3
13 2

1
b) 3.arcsen  arccos 11  
4
16 2

1 e
arctg
 2
x

1 e
  arctg

 2
x
 
 
 4
13. (Bb01, page 212, questão 389)
arctg7 x  1  arc sec2x  1
14. (Bb01, page 212, questão 390)
® 0
Calcule x na igualdade:
® 1/3
 4
5
Sejam   arcsen  um arco no segundo quadrante
  4
 um arco no quarto quadrante. Calcule o valor da expressão
 3 
e   arctg 
25. cos    .
15.
® 7
Sendo A= arctgx, B=arctg(1/x) e N=tg(A-B), calcule o valor de 20.N, para x=10.
16. Se arctg x  2  arctgx 
3 2
, x vale:
4
a) 1
b) 2
c) 3
d) 4
e) 5
17. (MACK-SP, Bb47)
a)
2
b)
2
3
18. (FCMSC-SP, Bb47)
  é:

2 2
O valor da tg  arcsen
3



c) 3 2
e)
d) 2 2
3 2
2
 3
 , então cos2  é:
Se   3.arcsen 

2


® 99
Funções Trigonométricas Inversas; Arquivo trigoinversas.dcs
a) –1
b) 
1
2
c) 0
d)
1
2
e) 1
19. O intervalo I  R que contém todas as soluções da inequação arctan
20. (ITA-2003)
Considerando as funções
—Page 6/9
1 x
1 x 
 arctan

2
2
6
Funções Trigonométricas Inversas; Arquivo trigoinversas.dcs
d)
/
—Page 7/9
Funções Trigonométricas Inversas; Arquivo trigoinversas.dcs
—Page 8/9
Aplicação
21. (Bb47)
Aparelhos elétricos, como motores, transformadores, reatores de
lâmpadas e outros, precisam, além da energia ativa (energia para o funcionamento
normal do aparelho), de uma forma de energia chamada reativa (para energizar as
partes elétricas do aparelho para sua efetiva utilização). As empresas controladoras
de energia medem um valor chamado fator de potência que relaciona as energias

mencionadas por meio da equação: FP  cos arctg

energia reativa 
 . As indústrias
energia ativa 
devem ter FP maior que 0,92, senão serão multadas pela má utilização da elétrica.
Suponhamos duas indústrias que consumam os seguintes valores:
a) indústria A: energia reativa — 1200 kvarh, energia ativa — 1200 kWh
b) indústria B: energia reativa — 1200 kvarh, energia ativa — 4800 kWh
Pergunta-se:
1) Qual das indústrias tem o melhor fator de potência?
® B; FP=0,9703
2) Qual das indústrias deve ser multada?
® A; FP=0,7071
22. (Bb47)
O fator de potência (FP) é um importante dado a respeito da otimização,
por uma empresa, do uso da energia elétrica. As concessionárias de energia medem

esse fator utilizando a equação: FP  cos arctg

energia reativa 
 , em que a energia
energia ativa 
reativa (necessária para energizar os equipamentos) é dada em kvarh e a energia
ativa (necessária para o funcionamento normal do equipamento), em kWh. Calcule
para cada uma das indústrias a seguir o fator de potência e determine qual delas tem
o uso mais racional de energia elétrica (maior FP).
a) indústria A: energia reativa =700 kvarh; energia ativa=1000 kWh
® 0,82
b) indústria A: energia reativa=800 kvarh; energia ativa =2000 kWh
® 0,93
c) indústria A: energia reativa=1200 kvarh; energia ativa=4000 kWh
® 0,96
d) Qual empresa é a mais racional?
23. (Bb47)
® empresa C tem maior FP

Sabendo que FP  cos arctg

kvarh, de uma indústria com FP 
® 1500 kvarh
energia reativa 
 , calcule a energia reativa, em
energia ativa 
2
e com energia ativa de 1500 kWh.
2
Funções Trigonométricas Inversas; Arquivo trigoinversas.dcs
—Page 9/9
Bibliografia
Bb54. Gentil, Marcondes, Greco, Bellotto, Sérgio — Matemática para o Segundo Grau —
Volume 2, 6ª. Edição, Editora Ática, 1997
Bb01. Iezzi, Gelson — Trigonometria — Volume 3, 7ª. Edição, Atual Editora, 1996.
Bb47. Scipione di Pierrô Netto, Sérgio Orsi Filho — QUANTA, Matemática em fascículos
para O Ensino Médio, Fascículo 4 — Editora Saraiva, 1ª. Edição, 2000.
Resolução
8. ?????
9.
arcsenx=arctg2x.
Fazendo a=arcsenx
22 sena 
e

3
3
,0,
R. S= 

2 
 2
a=arctg2x, temos: a=a  sena=x e tg a=2x
sena
1 

 0  sena. 2 
0
cos a
cos
a

10. Resolva
1
1
+ arc tg
2
3
a= arctg(1/2)  tga=1/2
a) y = arc tg
Fazendo:

4
b=arctg(1/3)  tgb=1/3
R.
e
y=a+b, aplicando tangente a ambos os membros: tgy=tg(a+b) 
1 1

tga  tgb
2
3  1  tgy  1  y  
tgy 

1 1
1  tga.tgb
4
1 .
2 3