1. Distribuição Gama - Milton Procópio de Borba

Distribuições Amostrais
por
Milton Procópio de Borba
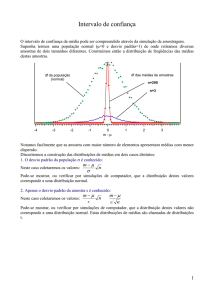
Se tirarmos várias amostras de uma população, em cada amostra, obteremos uma média da grandeza
estudada. Estas médias cumprem distribuições de probabilidades diversas, em torno da média desta grandeza, se
tomada na população.
Estas distribuições de probabilidade são úteis na inferência, tarefa de “transferir” para a população, os
resultados (média, desvio padrão e/ou porcentagens) obtidos na amostra
1. Distribuição Gama:
(y) -1 e-y/ 
f, (y) = 
, onde 
  ( )

é a função Gama, dada por  () =
Podemos verificar que que:  (n+1) = n. (n),  (1) =1, que  (1/2) =
e
 x  1
x
dx
, para cada  > 0.
0

e que para  inteiro,  (n+1) = n!
Propriedades: Média (= Valor esperado) = E(y) = 
Variância = Var(y) =  ² = ²
2. Distribuição ² (ver gráficos)
h (y) =
y /2-1e-y/2
, um caso particular da Distribuição Gama, com  =  /2 e  = 2.
2/2  ( / 2)
 ((  1)/2)
(1+t²/)-(+1)/2, para cada t real.
 ( / 2) 
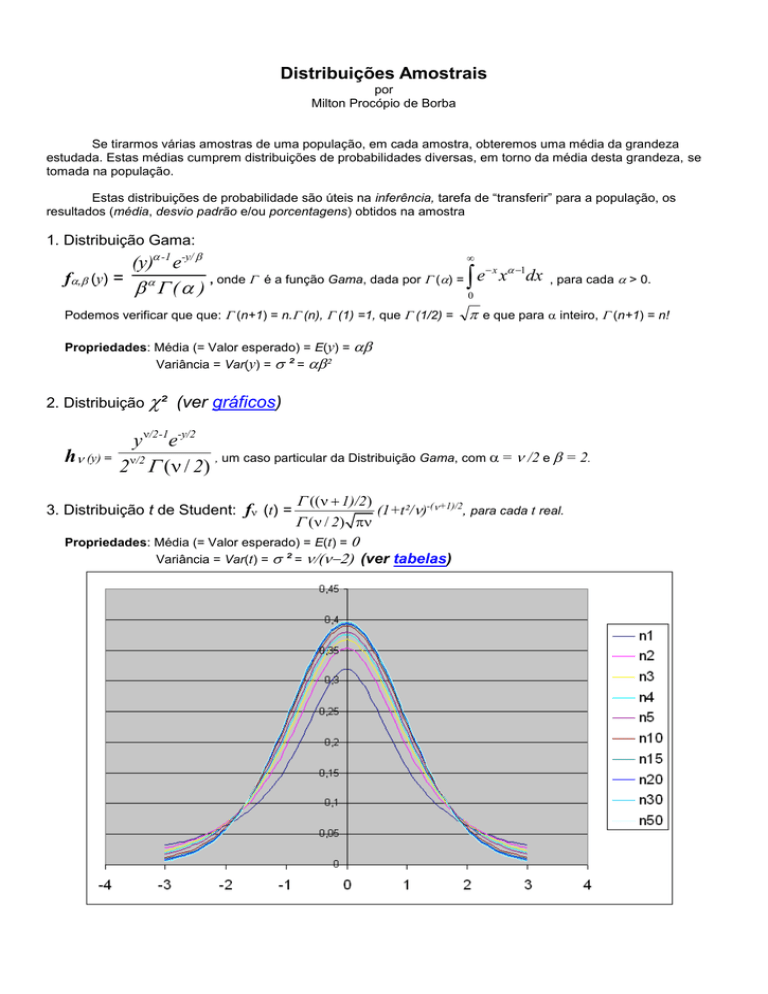
Propriedades: Média (= Valor esperado) = E(t) = 
Variância = Var(t) =  ² = (ver tabelas)
3. Distribuição t de Student: f (t) =