Disciplina: Estatística Profa. Neide Pinheiro MEDIDAS DE

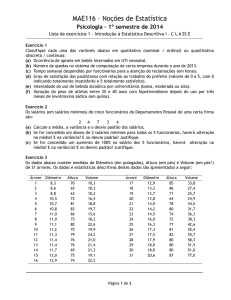
Disciplina: Estatística
Profa. Neide Pinheiro
MEDIDAS DE DISPERSÃO
A utilização de uma medida de tendência central – como representante de um
conjunto de dados – não descreve totalmente esse conjunto de dados.
Consideremos que duas cidades têm a média de temperatura diária de 24ºC.
Embora a temperatura seja, basicamente, a mesma nas duas cidades em uma
delas existem melhores condições para esportes aquáticos e para outras
atividades ao ar livre.
Na primeira cidade a temperatura oscila entre 21ºC e 27ºC durante todo o ano. Na
segunda cidade a temperatura, oscila de 4ºC a 38ºC no mesmo período – ou seja,
as piscinas nessa cidade não permanecem lotadas o ano todo. Constatado o fato,
precisamos de medidas que expressem as diferenças entre os valores desses
dados.
1. AMPLITUDE TOTAL
A mais simples das medidas de dispersão é a amplitude total. A amplitude total é a
diferença entre o maior e o menor valor de um conjunto de dados, ou seja...
A T = Max - min
Onde...
AT = amplitude total
Max = maior valor da distribuição
Min = menor valor da distribuição
EXEMPLO
Retornemos ao exemplo das cidades que têm a média de temperatura diária de
24º. A amplitude total da temperatura da primeira cidade é 27 - 21 = 6º. Já a
amplitude total da segunda cidade é 38 - 4 = 34º.
DESVANTAGENS
Como a amplitude total depende de dois valores do conjunto de dados – o maior e
o menor valor... Ela é altamente influenciada por valores extremos. Considerando
os salários de 50 empregados de uma empresa...Se o maior salário é R$ 2.800,00
e o menor salário, R$ 2.100,00, a amplitude total é...
AT = 2.800 - 2.100 = R$ 700,00
Essas são as medidas de dispersão.
Se a empresa precisar contratar um especialista sênior, cujo salário deve ser de
R$10.000,00, a amplitude passa a ser..
AT= 10.000 - 2.100 = R$ 7.900,00
Logo, o grande valor de amplitude não expressa, adequadamente, a
variabilidade dos dados, pois a maioria dos salários está no intervalo R$
2.100,00 a R$ 2.800,00.
VARIÂNCIA
A variância é expressa pela letra grega sigma ao quadrado “σ2‟‟ quando tratar-se
de população e “S²” quando tratar-se de amostra.
A variância – a mais importante das medidas de dispersão – é uma medida de
variabilidade que utiliza todos os dados de uma distribuição.
Em razão de suas propriedades matemáticas a média de um conjunto de dados é
uma informação relevante.
A variância é baseada na diferença entre o valor de cada observação e a média do
conjunto de dados.
Variância da Amostra
A fórmula da variância da amostra pode ser representada da seguinte forma...
DESVIO-PADRÃO DA AMOSTRA
A fórmula do desvio-padrão da amostra pode ser representada da seguinte
forma...
S = √ S² raiz quadrada da variância
Interpretação do desvio padrão
Regra Empírica
Para qualquer distribuição amostral com X e desvio padrão S, tem-se:
O intervalo X ± S contém entre 60% e 80% de todas as observações amostrais.
A porcentagem aproxima-se de 70% para distribuições aproximadamente de
70% para distribuições aproximadamente simétricas, chegando a 90% para
distribuições fortemente assimétricas.
COEFICIENTE DE VARIAÇÃO
Em algumas situações, podemos desejar obter uma medida que indique o
tamanho do desvio-padrão em relação à média – uma medida relativa.
Exemplo:
Em uma empresa, o salário médio dos homens é de R$ 4000, com desvio padrão
de R$ 1500, e o das mulheres é em média de R$ 3000, com desvio padrão de
R$1200.
Para os homens C.V = 1500/ 4000 = 0,375
Para as mulheres C.V = 1200 / 3000 = 0,4
Logo, podemos concluir que os salários das mulheres apresentaram maior
dispersão relativa que os dos homens. Para obtermos o resultado do C.V em
porcentagem multiplicamos o resultado por 100.
No caso:
C.V = para homens 37,5%
C.V = para mulheres 40%
Eis algumas regras empíricas para interpretações do coeficiente de variação:
Se C.V ≤ 15% tem-se baixa dispersão
Se 15% < C.V < 30% tem-se média dispersão
Se C.V ≥ 30% tem-se elevada dispersão