Problema 03

MEC2 - 98/99
ANÁLISE CINEMÁTICA DE MECANISMOS
3.1
Problema nº 03
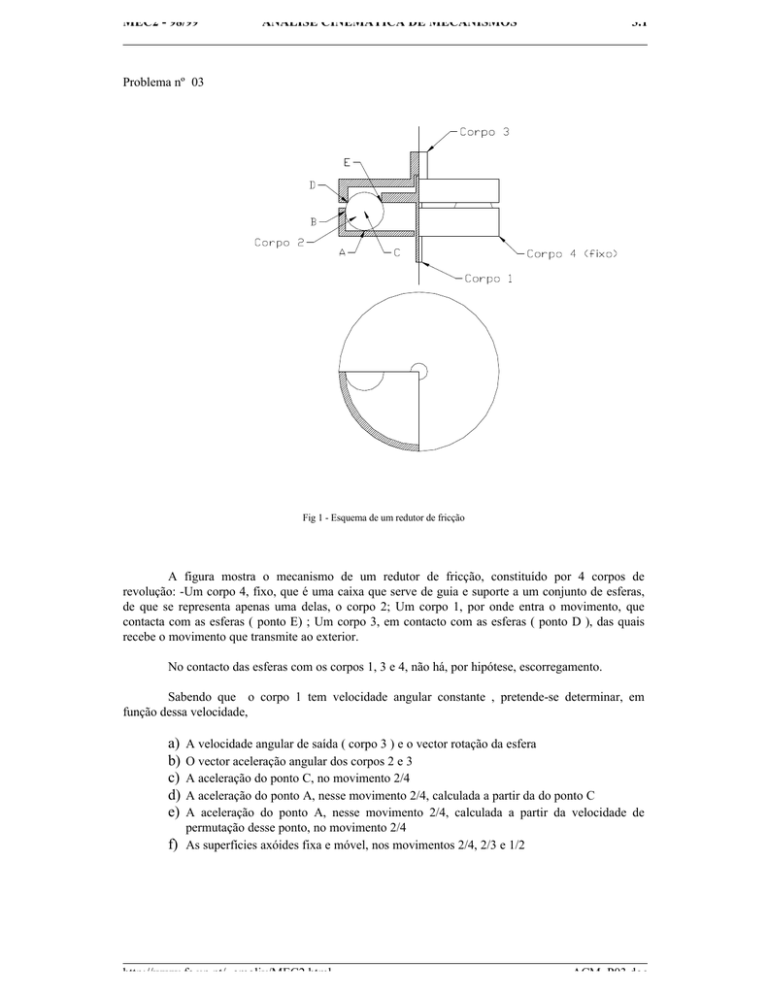
Fig 1 - Esquema de um redutor de fricção
A figura mostra o mecanismo de um redutor de fricção, constituído por 4 corpos de
revolução: -Um corpo 4, fixo, que é uma caixa que serve de guia e suporte a um conjunto de esferas,
de que se representa apenas uma delas, o corpo 2; Um corpo 1, por onde entra o movimento, que
contacta com as esferas ( ponto E) ; Um corpo 3, em contacto com as esferas ( ponto D ), das quais
recebe o movimento que transmite ao exterior.
No contacto das esferas com os corpos 1, 3 e 4, não há, por hipótese, escorregamento.
Sabendo que o corpo 1 tem velocidade angular constante , pretende-se determinar, em
função dessa velocidade,
a)
b)
c)
d)
e)
A velocidade angular de saída ( corpo 3 ) e o vector rotação da esfera
O vector aceleração angular dos corpos 2 e 3
A aceleração do ponto C, no movimento 2/4
A aceleração do ponto A, nesse movimento 2/4, calculada a partir da do ponto C
A aceleração do ponto A, nesse movimento 2/4, calculada a partir da velocidade de
permutação desse ponto, no movimento 2/4
f) As superfícies axóides fixa e móvel, nos movimentos 2/4, 2/3 e 1/2
http://www.fe.up.pt/~cmoliv/MEC2.html
ACM_P03.doc
MEC2 - 98/99
ANÁLISE CINEMÁTICA DE MECANISMOS
3.2
RESOLUÇÃO
a) Velocidade angular de saída ( corpo 3 ) e o vector rotação da esfera
Nos pontos de contacto da esfera com o corpo 4, porque não há escorregamento, a velocidade
no movimento 2/4 é nula. Por eles passa, por conseguinte, o eixo instantâneo de rotação desse
movimento.
Fig 2 - Definição dos eixos instantâneos de rotação
O ponto O de intersecção dos EIR dos movimentos 2/4 e 1/4 tem velocidade nula no
movimento 1/2 . O EIR do movimento 1/2 passa portanto por O e E.
O ponto O de intersecção dos EIR dos movimentos 1/2 e 1/3 tem velocidade nula no
movimento 2/3 . O EIR do movimento 2/3 passa portanto por O e D.
Conhecido o movimento do corpo 1 e atendendo à ausência de escorregamento nos pontos de
contacto com a esfera, podemos escrever
→
r
r
v E 14 = w14 × OE
(1)
→
→
r
r
w 24 × AE = w14 × OE
→
(2)
→
r
r
w 24 × AD = w 34 × OD
(3)
r
r
A equação (2) permite calcular w 24 e a equação (3) dá-nos w 34
Notemos que o centro da esfera ( C ) e o eixo de simetria de revolução dos corpos 1, 3 e 4,
permitem definir um plano meridiano da esfera, que contém sempre os pontos de contacto desta com o
exterior ( pontos A, B, D e E ). Este plano tem movimento de rotação em torno do eixo de simetria de
revolução. Vamos considerar um espaço rígido ligado a este plano, a que atribuiremos a designação de
S5.
Vai ser nesse referencial S5 que iremos projectar todos os vectores anteriormente referidos,
pelo facto de, nesse referencial, os vectores de posição terem componentes independentes do tempo.
http://www.fe.up.pt/~cmoliv/MEC2.html
ACM_P03.doc
MEC2 - 98/99
ANÁLISE CINEMÁTICA DE MECANISMOS
3.3
Fig 3 - Definição geométrica
Projectando em S5, obteremos
sendo
π

R1

w 24 cos 4   − r cos θ   0  


 
 
 
0
0
0


×
=  0 ×
 w sin π  r + r sin θ w  R 2 + r + r sin θ

  14  

 24
4 
(4)
π

R3

w 24 cos 4   + r cos β   0  


 
 
 
0
0
0


×
 =  0 ×
 w sin π  r + r sin β w  R 2 + r + r sin β

  34  

 24
4 
(5)
 R2 − R1
 R 3 − R2 
θ = a cos
 e β = a cos





r
r
w 24 = −
w 34 =
R1
w 14
( r + r sin θ) cos( π / 4) + r cos θ sin( π / 4)
R1 ( r + r sin β) cos( π / 4) − r cos β sin( π / 4)
w 14
R3 ( r + r sin θ) cos( π / 4) + r cos θ sin( π / 4)
(6)
(7)
Fig 4 - Composição de vectores rotação
http://www.fe.up.pt/~cmoliv/MEC2.html
ACM_P03.doc
MEC2 - 98/99
ANÁLISE CINEMÁTICA DE MECANISMOS
3.4
b) Vector aceleração angular dos corpos 2 e 3
Para calcular o vector aceleração angular, basta-nos derivar o vector rotação em ordem ao
tempo, relativamente ao corpo 4 (fixo).
Atendendo a que os vectores são conhecidos pela sua projecção em S5, teremos
r
r•
r
r
α 24 = ( w 24 ) / S + w54 × w 24
(8)
r
r•
r
r
α 34 = ( w 34 ) / S + w 54 × w 34
(9)
5
5
Sendo, por hipótese, constante o valor de w14, teremos
0
0  0  w 24 cos( π / 4) 

r
  
 
 

α 24 = 0 +  0  × 
0
 = w 54 w 24 cos( π / 4)
0 w   w sin( π / 4)  

0
   54   24
 

(10)
0  0   0  0
r
  
 
  
α 34 = 0 +  0  ×  0  = 0
0 w  w  0
   54   34   
(11)
r
em que w 54 resulta do cálculo da velocidade do centro da esfera, ou seja
 0   R2  w 24 cos( π / 4)  0
  
 
 

0
 × 0
 0 × 0  = 
w  R 2 + r   w sin( π / 4)   r 
  
  24
 54  
w 54 = −
r cos( π / 4)
w 24
R2
(12)
(13)
c) Aceleração do ponto C, no movimento 2/4
Como O é um ponto fixo, podemos fazer
→
→ 
r
r
r
r
a C 24 = α 24 × OC+ w 24 ×  w 24 × OC


(14)
0

  R 2  w 24 cos π / 4  w 24 cos π / 4  R2 

 
 
 
 

0
0
w 54 w 24 cos( π / 4)  ×  0  + 
 × 
 ×  0 

 R2 + r   w sin π / 4    w sin π / 4  R 2 + r 
0

 
  24
   24
 

(15)
Como o ponto C também pertence ao referencial S5, será ainda mais fácil calcular a sua
aceleração a partir do movimento 5/4. Teremos, para C, um movimento de rotação uniforme, pelo que
a sua aceleração é imediatamente conhecida e igual a
http://www.fe.up.pt/~cmoliv/MEC2.html
ACM_P03.doc
MEC2 - 98/99
r
a C54
ANÁLISE CINEMÁTICA DE MECANISMOS
− w 254 R2


=
0



0


3.5
(16)
d) Aceleração do ponto A, no movimento 2/4, calculada a partir de C
→
→ 
r
r
r
r
r
a A 24 = a C 24 + α 24 × CA + w 24 ×  w 24 × CA


2
− w 54

R2 
0

 

r
a A 2a = 
0
 + w 54 w 24 cos( π / 4)  ×

 

0
0

 

(17)
 0 
 
 0 +
− r 
 
(18)
w 24 cos π / 4   w 24 cos π / 4  0 

 
  
0
0
+
 × 
 ×  0 
 w sin π / 4    w sin π / 4  − r 
 24
   24
  
r
a A 24
2
− w 54
R2 − w 54 w 24 r cos π / 4 − w 224 r sin π / 4. cos π / 4


=
0

2
2


w
r
4
cos
π
/
24


2
− w 24 r sin π / 4.cos π / 4 


=
0

2
2


w 24 r cos π / 4


(19)
e) Aceleração do ponto A, nesse movimento 2/4, calculada a partir da velocidade de permutação
desse ponto, no movimento 2/4
→ 
r
r
r
r
r
r
r
a A 24 = VA 24 × w 24 = v A 54 × w 24 =  w 54 × OA × w 24


  0  R 2  w 24 cos π / 4

r
   

a A 24 =   0  ×  0  × 
0
=
 w  R   w sin π / 4 
  54   2   24

(20)
 0  w 24 cos π / 4

 

0
w 54 R2 × 
=
 0   w sin π / 4 

  24

(21)
−
/ 4 cos π / 4


0


 + w 2 r cos2 π / 4 
24


f) As superfícies axóides fixa e móvel, nos movimentos 2/4, 2/3 e 1/2
 + w 54 R 2 w 24 sin π / 4 


=
0
=
− w R w cos π / 4 
54 2 24


w 224 r sin π
Atendendo ao que anteriormente foi dito acerca de o referencial S5 ser definido a partir do
plano meridiano da esfera que passa pelo eixo vertical OF, todos os eixos instantâneos de rotação são
fixos a este referencial.
http://www.fe.up.pt/~cmoliv/MEC2.html
ACM_P03.doc
MEC2 - 98/99
ANÁLISE CINEMÁTICA DE MECANISMOS
3.6
Os movimentos de permutação podem então definir-se a partir do movimento deste
referencial S5.
Assim, no movimento 2/4 , a permutação do EIR ( que contém A e B ) gerará uma superfície
cónica de eixo OE, quando observado a partir de S4 e uma outra superfície cónica de eixo OC, quando
observado de S2.
No movimento 2/3 , a permutação do EIR ( que contém O e D ) gerará uma superfície cónica
de eixo OE, quando observado a partir de S3 e uma outra superfície cónica de eixo OC, quando
observado de S2.
No movimento 1/2 , a permutação do EIR ( que contém O e E ) gerará uma superfície cónica
de eixo OE, quando observado a partir de S1 e uma outra superfície cónica de eixo OC, quando
observado de S2.
A figura 4 mostra estas superfícies axóides\
Fig 4 - Supefícies axóides nos movimentos 2/4, 2/3 e 1/2
http://www.fe.up.pt/~cmoliv/MEC2.html
ACM_P03.doc