LIMITE DE UMA FUNÇÃO A UMA VARIÁVEL REAL NOÇÃO

LIMITE DE UMA FUNÇÃO A UMA VARIÁVEL REAL
NOÇÃO INTUITIVA DE LIMITE
Intuitivamente, falar que o limite de uma função f(x), quando x tende a p, é igual a L, o
qual escrevemos simbolicamente:
significa que quando x se aproxima de p, tanto pela direita, quanto pela esquerda, o
valor da função se aproxima de L.
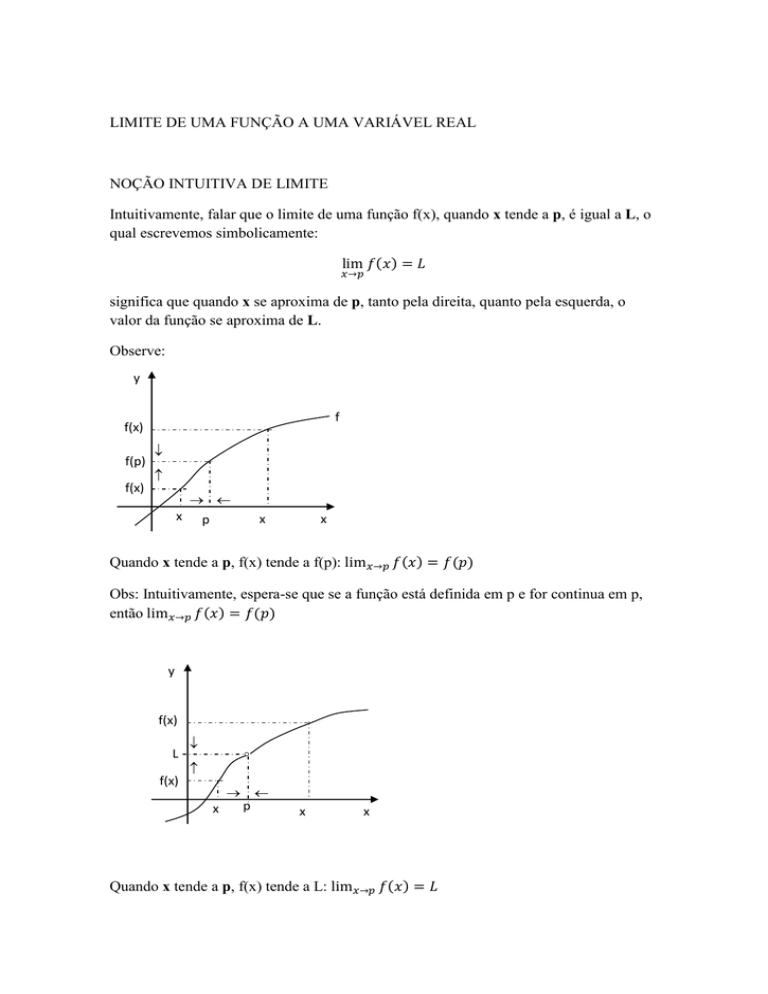
Observe:
y
f
f(x)
f(p)
f(x)


 
x
x
p
x
Quando x tende a p, f(x) tende a f(p):
Obs: Intuitivamente, espera-se que se a função está definida em p e for continua em p,
então
y
f(x)
L
f(x)



 
p
x
x
Quando x tende a p, f(x) tende a L:
x
Por outro lado, se f não é continua em p e
deveria ter em p.
, então L será o valor que f
Veja o exemplo abaixo:
Seja a função f(x) = 2x +1. Vamos atribuir valores para x proximos de 1, pela sua
direita ( Valores maiores que 1 ) e pela sua esquerda ( Valores menores que 1 ), e em
seguida, calcular y.
x
y = 2x + 1
x
y = 2x + 1
1,5
4
0,5
2
1,3
3,6
0,7
2,4
1,1
3,2
0,9
2,8
1,05
3,1
0,95
2,9
1,02
3,04
0,98
2,96
1,01
3,02
0,99
2,98
y
y= 2x + 1
3
0
x
1
À medida que x se aproxima de 1, y se aproxima de 3, ou seja, quando x tende a 1
( x  1 ), y tende a 3 ( y  3 ), então temos a notação:
DEFINIÇÃO FORMAL DE LIMITE:
Seja um intervalo aberto I, contendo p, e seja f(x), uma função definida em I, exceto
possivelmente no próprio p. Dizemos que o limite de f(x) quando x se aproxima de p é
igual a L, cuja notação é
, se para todo  > 0 dado, existir um  > 0 tal
que, para todo x  I, temos:

Tal número L, que quando existe é único, será indicado por
Analise os gráficos abaixo:
a)
y
f
L+
L

L-
p- p
P+
x
f não está definida em p, mas existe L que satisfaz a propriedade:
para todo  > 0 dado, existe um  > 0 tal que, para todo x  I,

b)
y
f(p)
f
L+
L

L-
p- p
P+
x
f está definida em p, mas não é continua em p. No entanto, existe L que satisfaz a
propriedade acima
c)
y
f
L+
L
L-
p- p
x
P+
f é continua em p, desta maneira f(p) = L satisfaz a propriedade acima
a)
y
f

p
x
não existe L que satisfaz a propriedade:
Vejamos, abaixo, um exemplo da definição acima:
“Usando a definição acima, prove que
”
De acordo com a definição acima, precisamos provar que:
para todo  > 0 dado, existe um  > 0 tal que,
sempre que
Assim:
Como
então
, de modo que existe o
Exemplos:
1 )Seja a função
, calcule o
como x² + x – 2 = ( x – 1 ).( x + 2 ) 
f(x)
( x  1).( x  2)
; x 1
x 1
Podemos notar que para x  1, f(x)  3, embora para x = 1, f(x) = 2  3 . Ocorre no
entanto que procuramos o comportamento da função para ( x  1 ), logo temos
Comprovando:
Se g : R  R e g(x) = x + 2 ,
g(x) =
( x + 2 ) = 1 + 2 = 3 , embora g(x) 
f(x) em x = 1. No entanto, ambas têm o mesmo limite.
y
f(x)
3
2
0
x
1
2 ) Calcule o
Nota-se a impossibilidade de calcularmos
Trocamos então
x2  4
para x = 2 ( Indeterminação ).
x2
x2  4
por x + 2 , possibilitando assim o cálculo quando x tende a 2.
x2
3 ) Calcule o
PROPRIEDADES DOS LIMITES
Proposição. Se
então:
I)
Exemplo :
II)
Exemplo :
exitem, e c é um numero rela qualquer,

=

III )
Exemplo :
[ f(x) . g(x) ] =
f(x) .
( -x² . log x ) =
g(x)
-x² .
log x = -10² . log 10 = -100 . 1 = - 100
IV)
Exemplo :
V)
, n  N*
=
Exemplo :
, n  *  f ( x)  0 .( Se f(x)  0, n é ímpar )
VI )
Exemplo :
lim
x2
x3  x2 1

lim
x2
x3  x2 1
 2 3  2 2  1  8  4  1  11
VII )
Exemplo :
VIII )
Exemplo :
8)
Exemplo :
Exercícios :
1 ) Calcular :
a)
b)
lim
(2 x 2  3x  4) 
x2
lim
x 1
k ) lim
t o
x 2  5x  4

x 1
l ) lim
t 0
25  3t  5

t
(4  t ) 2  16

t
c ) lim
x 1
x 3  3x  2
x2 1 
x0
e ) lim
x 1
f)
x 1
g)
h)
lim
(cos x  sen x)
x0
i ) lim
x2
x0
x4 1
lim
o)
x5 1 
x 1
4
x 1 
( x 2  3x  4)
x3  8
x2  4 
1 x  1 x

x
n ) lim
x 1
x  1
lim
x  1
x4 1
x3 1 
3
lim
lim
m)
x3 3

x
d ) lim
x 2  3x  2
x2 1 
lim
p)
h 1


q ) lim
x 1
r ) lim
x0
j ) lim
h 1
5
h 1
h 1 
x 3  3x 2  3x  1

x 1
b 2  at  b
;b  0 
t
h 1
h 1 
BIBLIOGRAFIA:
FLEMMING, D.M. ; GONÇALVES, M.B. Cálculo A. São Paulo: Pearson Education,
2001
GUIDORIZZI, H.L. Um curso de cálculo vol 1. São Paulo: LTC, 2001
SIMMONS, G. F. Cálculo com Geometria Analítica vol1. São Paulo: Pearson
Education, 1988
STEWART, J. Cálculo vol 1. São Paulo: Cengage Learning, 2009
THOMAS, G.B. Cálculo vol1, São Paulo: Addison Weslwy, 2009