Segmentos proporcionais - Colégio Alexander Fleming
Propaganda
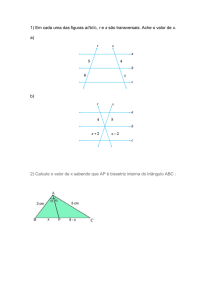
Segmentos proporcionais Profor Marco Cezar Teorema de Tales Se duas retas são transversais de um conjunto de retas paralelas, então a razão entre dois segmentos quaisquer de uma delas é igual à os segmentos razão entre correspondentes da outra. a c a+c = = b d b+d Teorema da bissetriz interna Em qualquer triângulo, uma bissetriz interna (bissetriz de um ângulo interno) divide o lado oposto em segmentos proporcionais aos lados adjacentes. a b c d Teorema da bissetriz externa Em qualquer triângulo a bissetriz de um ângulo externo intercepta o prolongamento do lado oposto e o divide em dois segmentos subtrativos proporcionais aos lados adjacentes. a b m n Semelhança de triângulos Dois triângulos são semelhantes se, e somente se, possuem os três ângulos ordenadamente congruentes e os lados homólogos proporcionais. ∆ ADE ~∆ A’B’C’ Os triângulos ABC e A’B’C’ são semelhantes 1º ângulos correspondentes sejam congruentes: ^ = A’; ^ B ^ = B’ ^ eC ^ = C’ ^ A 2º lados homólogos sejam proporcionais: AB BC AC k = = = A’B’ B’C’ A’C’ Teorema fundamental Se uma reta é paralela a um dos lados de um triângulo e intercepta os outros dois lados em pontos distintos, então o triângulo que ela determina é semelhante ao primeiro. DE // BC ∆ ADE ~∆ ABC
