IPH 01107 3a LISTA DE EXERCÍCIOS (atualizada

IPH 01107
3a LISTA DE EXERCÍCIOS
(atualizada 2017/1)
Sempre que necessário e não for especificado, utilize:
ρH2O = 1000 kg/m3
ρar = 1,2 kg/m3
6
ReynoldsCRÍTICO = 3.10
µágua = 10-3 kg/(m.s)
µar = 1,8.10-5 kg/(m.s)
g = 9,8 m/s2
1a PARTE = CAMADA LIMITE
1.1) Considere um escoamento com U = 0,305 m/s ao longo de uma placa plana
de 0,305 m de comprimento. Quando o fluido for: (a) ar e (b) água, calcule a
espessura da camada limite no final da placa para os dois casos.
R: δL(ar) = 19,5 mm ; δL(água) = 5,0 mm.
1.2) Uma barcaça com dimensões 30,5 m X 12,2 m move-se à velocidade de
o
1,03 m/s em água doce com temperatura de 14 C, como mostra a figura. Estimar
a resistência devido ao efeito viscoso usando a teoria de placa plana
(desconsiderar o arrasto na frente da barcaça).
Dados: ρ = 999 kg/m3 ; ν14oC = 1,1724.10-6 m2/s
R: D = 472 N
1.3) Uma placa fina e lisa é presa na parte lateral de um caminhão como mostra a
figura. Estime o arrasto sobre a placa quando o caminhão é conduzido a 88 km/h.
R: 6,2 N
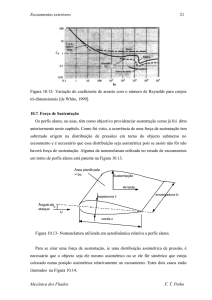
1.4) O dispositivo da figura foi projetado para medir tensão de cisalhamento na
parede quando ar escoa sobre a parede lisa com velocidade livre U. A proposta é
que τw possa ser obtida medindo-se o momento M na base do suporte do
pequeno elemento de superfície quadrada. Faça um gráfico M x U para 5 < U < 50
m/s, com l = 2, 3, 4 e 5 m.

 L
l  
R: C.L. laminar: l = 2 m e U < 7,2 m/s com M =  0,664 ρ ar U 2 b  1 / 2 − 1 / 2  d 

ℜ l  
ℜL

onde d = CG da haste até centro de giro, l = distância até o início da placa e L até
o fim e b = largura da placa. Para os outros casos

 L
l  
M =  0,037 ρ ar U 2 b  1 / 5 − 1 / 5  d 

ℜ l  
ℜL

1.5) As camadas limites da atmosfera são bem espessas mas seguem fórmulas
semelhantes às da teoria de placas planas. Considere o vento soprando a 10 m/s
a uma altura de 80 m acima de uma praia plana. Estime a tensão de cisalhamento
do vento (em Pa) na praia se o ar está nas condições de atmosfera padrão. Qual
será a velocidade do vento a 17 cm e a 170 cm ?
OBS: Utilize a distribuição logarítmica de velocidades para fundo liso com K=0,41
e B=5,0.
R: τw = 0,078 Pa; u = 6,38 m/s e 7,84 m/s.
1.6) Uma camada limite atmosférica é formada quando o vento sopra sobre a
superfície terrestre. O perfil de velocidades nesta camada pode ser dado por uma
lei exponencial u = a.yn, onde as constantes a e n dependem da rugosidade do
terreno. Para áreas urbanas, n=0,4; para áreas com matas ou suburbanas, n=0,28
e para campo aberto, n=0,16. Pede-se:
(a) Se a velocidade é de 6,1 m/s na base de uma vela de barco (y=1,22 m), qual
será a velocidade no topo do mastro (y=9,15 m) ?
(b) Se a velocidade média no 10o andar de um prédio em uma zona urbana é de
4,44 m/s, qual será a velocidade média no 6o andar (cada andar tem 3 m de
altura) ?
R: 8,42 m/s ; 3,62 m/s
1.7) Um prédio de 15 andares (cada andar com 3,66 m de altura) é construído em
um parque industrial suburbano.
(a) Faça um gráfico da pressão dinâmica (ρ.u2/2) como função da elevação se o
vento sopra como um furacão de 33,33 m/s no topo do edifício (utilize dados do
exercício anterior);
(b) Se no 15o andar existe uma janela de 3 m X 3 m, calcule a força do vento
sobre a mesma.
R: p[Pa] = 72,27.y[m]0,56 ; 6129 N
2a PARTE = ARRASTO SOBRE CORPOS SUBMERSOS
2.1) Um pilar de seção transversal quadrada com 0,20 m de lado encontra-se
mergulhado em água do mar que escoa com velocidade de 1,5 m/s. Estime o
máximo momento de flexão exercido pelo escoamento em relação à base do pilar.
Dados: ρmar = 1024 kg/m3 ; νmar = 1,023.10-6 m2/s ; CD: verificar situações.
R: 6518 J
2.2) Um carro de alta velocidade (“dragster”) com massa de 2000 kg, CD = 0,3 e
A = 1 m2 usa um paraquedas de 2 m de diâmetro para desacelerar de uma
velocidade inicial de 100 m/s. Assumindo os CD constantes, e desprezando a
resistência de rolamento e o uso do freio, calcule a distância percorrida e a
velocidade do carro após 1, 10, 100 e 1000 segundos, a partir da desaceleração.
Dado: CDparaqueda (tab. 2.c) = 1,2
R.: 94; 649; 2080 e 3865 m ; 88,9; 44,4; 7,4 e 0,8 m/s
2.3) Duas bolas lisas (D = 7,35 cm) são conectadas a um cabo de 6 mm de
diâmetro e 56 cm de comprimento que gira em torno de seu centro a 250 rpm.
Que potência (em Watt) é necessária para manter esta rotação ? Incluir arrasto
sobre o cabo (assumindo U = constante = Umédio sobre o cabo) e assumir o ar
padrão ao nível do mar. Dado: νar = 1,51.10-5 m2/s; Pot = M . ω
R.: 9,8 W
2.4) Uma bola de ping-pong tem massa de 2,6 g e diâmetro de 3,8 cm. Ela pode
ser suportada por um jato de ar que sai de um aspirador de pó como mostra a
figura. Para ar padrão qual a velocidade necessária ?
R.: 9,6 m/s
2.5) Uma esfera pesada conectada a uma corda deve pender com um ângulo θ
quando imersa em um fluxo de ar com velocidade U. Pede-se:
(a) Determine uma expressão para θ = f(propriedades do escoamento e da
esfera).
(b) Determine θ para Desfera = 3 cm, desfera = 7,86, Uo = 40 m/s. Despreze o arrasto
sobre a corda.
8 Reg ρe
o
R.: tan θ =
; 72
2
3 C DU0
ρf
2.6) Um vento de 26,84 m/s sopra sobre uma torre como esquematizada na
figura. Estime o momento M necessário na base para evitar que a torre caia.
Dados: CD(esfera) = 0,3 e CD(coluna) = 0,7.
R.: 495 kN.m
2.7) Uma bola de golfe (DG = 4,3 cm W G = 0,441 N) pode se deslocar à velocidade
de UG= 61 m/s ao deixar o taco. Uma bola de tênis (DT = 7,62 cm; W T = 0,0245 N)
pode se deslocar à velocidade de UT = 18,3 m/s ao deixar a raquete. Pede-se:
(a) determine o arrasto sobre uma bola de golfe padrão (CD = 0,25); uma
bola de golfe lisa (CD= 0,51) e uma bola de tênis (CD = 0,5).
(b) determine a desaceleração para cada bola nas condições acima.
R.: 0,828 N; 1,689 N; e 0,468 N. -18,42 m/s2; -37,57 m/s2; -187,4 m/s2.
2.8) Se, para um dado veículo, necessitamos de 30 HP para vencer o arrasto
aerodinâmico quando o mesmo é dirigido a 88 km/h, estime a potência necessária
a 104 km/h.
R.: 49,5 HP
2.9) Um bagageiro retangular de 48,8 cm de altura, 1,525 m de comprimento e
1,281 m de largura é preso à capota de um carro. Estime a potência adicional
necessária para dirigir o carro com o bagageiro à velocidade de 96 km/h através
do ar parado. (Utilize CD cubo = 1,07, por limitação das tabelas fornecidas.)
R.: 10 HP
2.10) Uma esfera de aço (d = 7,9) com 50 mm de diâmetro é largada de um avião.
o
Assumindo condições atmosféricas padrão (t = 20 C; patm = 101 kPa), qual será a
velocidade "terminal" da esfera ?
R.: 220 m/s
3a PARTE = ESCOAMENTO EM CONDUTOS SOB PRESSÃO
3.1) Um óleo com ρ = 900 kg/m3 e ν = 0,0002 m2/s escoa através de um conduto
inclinado, com diâmetro de 50 mm, como mostra a figura. Assumindo o
escoamento como em regime laminar pede-se:
a) verificar o sentido do escoamento;
b) calcular a perda de carga entre as seções 1 e 2;
c) calcular velocidade média e Re; e
d) verificar se o escoamento é, realmente, laminar.
R.: 1 para 2; hf = 4,91 m; 1,88 m/s; 470; laminar
2
10 m
p2=250 kPa
?
40o
1
p1=350 kPa
3.2) Ar escoa através de um conduto com 14 cm de diâmetro em condições de
pleno desenvolvimento e a velocidade na linha central é de 5 m/s. Estimar:
a) u*, τw;
b) perda de carga entre duas seções distantes de 100 m; e
c) velocidade média.
Obs.: Partir da suposição de que o escoamento seja turbulento e usar a lei
-5
2
3
logarítmica de velocidades e usar νar = 1,46.10 m /s e ρar = 1,205 kg/m
R.: = 0,227 m/s; 0,062 Pa; 15 m; 4,17 m/s.