π π π - Páginas Pessoais

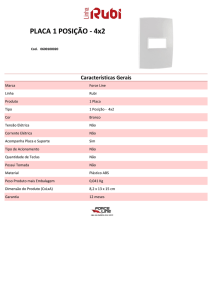
Universidade Federal do Paraná
Setor de Tecnologia
Aluno: _______________________________________________________________________________________
Matrícula: ________________________________________________ Data: ____________________________
TH 705 - MECÂNICA DOS FLUIDOS AMBIENTAL II
TRABALHO DE CASA #3
ORIENTAÇÕES: ESTA FOLHA DEVERÁ SER DEVOLVIDA COMO FOLHA DE ROSTO DO TRABALHO. AS QUESTÕES
DEVERÃO SER DESENVOLVIDAS EM FOLHAS DE PAPEL SULFITE. A DATA DE ENTREGA É 11/09/2015.
1. Para escoamento em camada limite turbulenta sobre placa plana lisa de largura
infinita, a componente longitudinal da velocidade, 𝑢, na região muito próxima a
placa, conhecida como sub-camada laminar, pode ser correlacionada com a tensão
de cisalhamento na placa, 𝜏𝑤 , com a distância normal a partir da placa, y, e com as
propriedades do fluido, 𝜌 e 𝜇. Utilize o teorema  de Buckingham para demonstrar
que a correlação pode ser escrita como,
𝑢+ = 𝑦 + ,
onde 𝑢+ = 𝑢⁄𝑢∗ e 𝑦 + = 𝑦 𝑢∗⁄𝜈 , sendo 𝑢∗ = (𝜏𝑤 ⁄𝜌)1⁄2 chamada de velocidade
de atrito (𝐿𝑡 −1 ).
2. Uma bola de tênis quando golpeada na sua parte superior poderá girar rapidamente
de modo que apareça uma força de sustentação para baixo. Esta força FL é função
da frequência de rotação da bola, , da velocidade de golpe na bola, V, do diâmetro
da bola, D, e das propriedades do fluido,  e .
(a) Aplique o teorema  de Buckingham para encontrar a relação 𝜋1 = 𝑓(𝜋2 , 𝜋3 ).
Use V, D como variáveis repetentes, de modo que FL apareça em 𝜋1, 
apareça em 𝜋2 e  apareça em 𝜋3 .
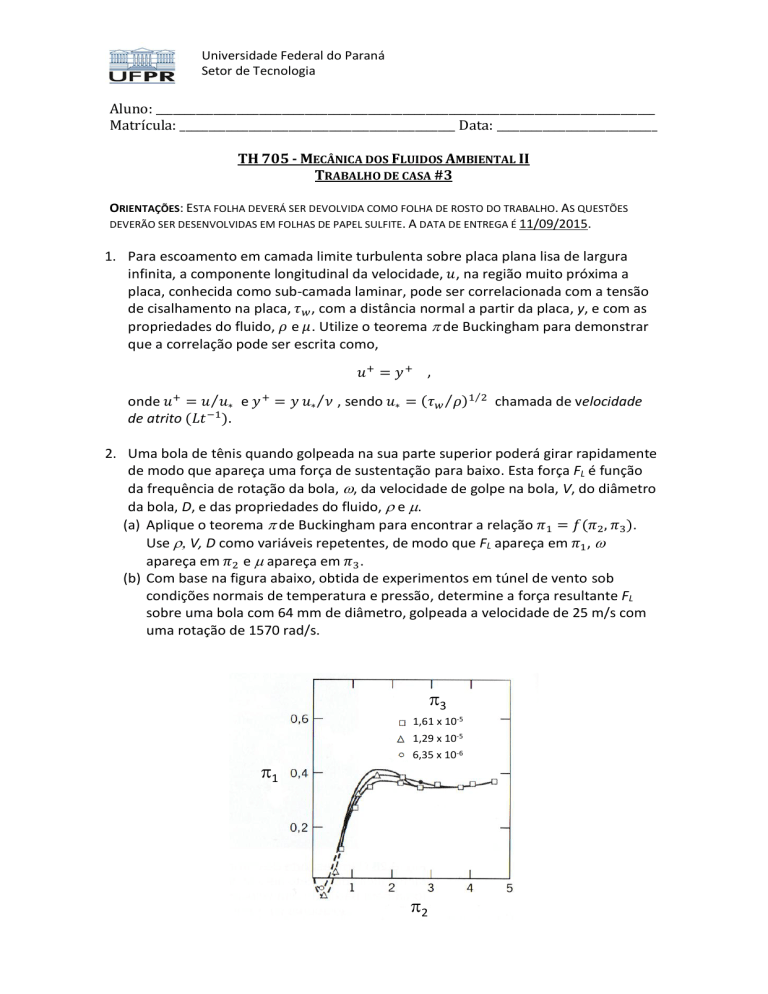
(b) Com base na figura abaixo, obtida de experimentos em túnel de vento sob
condições normais de temperatura e pressão, determine a força resultante FL
sobre uma bola com 64 mm de diâmetro, golpeada a velocidade de 25 m/s com
uma rotação de 1570 rad/s.
3
1,61 x 10-5
1,29 x 10-5
1
6,35 x 10-6
2
3. As equações governantes de um escoamento convectivo próximo a uma placa
vertical aquecida, de espessura infinita, para fluido Newtoniano e incompressível,
escrevem-se,
u v

0
x y
u
,
  2u  2u 
u
u
v
 g T  T1     2  2 
x
y
y 
 x
  2T  2T 
 T
T 
  k  2  2 
v
y 
y 
 x
 x
c p  u
,
.
Escreva as equações acima na forma adimensional. Identifique os parâmetros
adimensionais presentes no problema. Utilize as variáveis adimensionais,
u* 
uL

,
v* 
vL

,
x* 
x
,
L
y* 
y
,
L
T* 
T  T1
,
T0  T1
onde L é o comprimento da placa, To é a temperatura da placa, T1 é a temperatura
longe da placa e  é uma constante.
4. Uma pessoa observa um aparelho de ar condicionado que pinga água sobre o
parapeito de uma janela. Quando não há vento as gotas caem verticalmente na
posição x=0. Em dia de vento observou-se que as gotas tocam o parapeito em x=L.
Estime a velocidade do vento. Considere primeiramente que as gotas sejam
suficientemente pequenas que a lei de Stokes para a força de arrasto possa ser
utilizada. Verifique se esta hipótese pode ser usada e, caso não seja válida, obtenha
uma nova solução aplicando uma lei de arrasto adequada. Considere que o vento
sopra na horizontal com velocidade constante. Depois de obter uma solução literal,
utilize os seguintes dados para obter uma estimativa numérica da velocidade do
vento: H=2m, L=1m, d=1mm (diâmetro das gotas consideradas esféricas).
5. Considere escoamento de fluido Newtoniano e incompressível em uma camada
limite laminar sobre placa plana lisa de espessura infinita. Escreva as equações de
conservação de massa e de quantidade de movimento e mostre as simplificações
possíveis para se obter as chamadas equações da camada limite. Reproduza a
solução de Blasius para a distribuição de velocidade, a espessura da camada limite,
o coeficiente de atrito e de arrasto.
6. Considere uma placa plana lisa de espessura infinita posicionada na horizontal
submersa em um escoamento na atmosfera sob velocidade do vento uniforme de 1
e 10 m/s. (a) Estime a espessura da camada limite a uma distância de 1 e 5 m do
bordo de ataque para os dois casos. Quais das duas velocidades do vento fornece a
maior espessura da camada limite? (b) Estime a tensão de cisalhamento na placa
para os dois casos.
7. Ar em CNTP escoa sobre uma placa plana lisa com velocidade de aproximação igual
a 3,1 m/s. Estime a distância em relação ao bordo de ataque da placa em que
ocorre a transição do regime laminar para o turbulento e estime a espessura da
camada limite neste local.