Movimento Harmônico Simples – MHS

Movimento Harmônico Simples – M.H.S.
1. Introdução
É o movimento periódico no qual a aceleração é proporcional a
posição. Por exemplo: sistema massa-mola e pêndulo simples.
2. Cinemática do M.H.S.
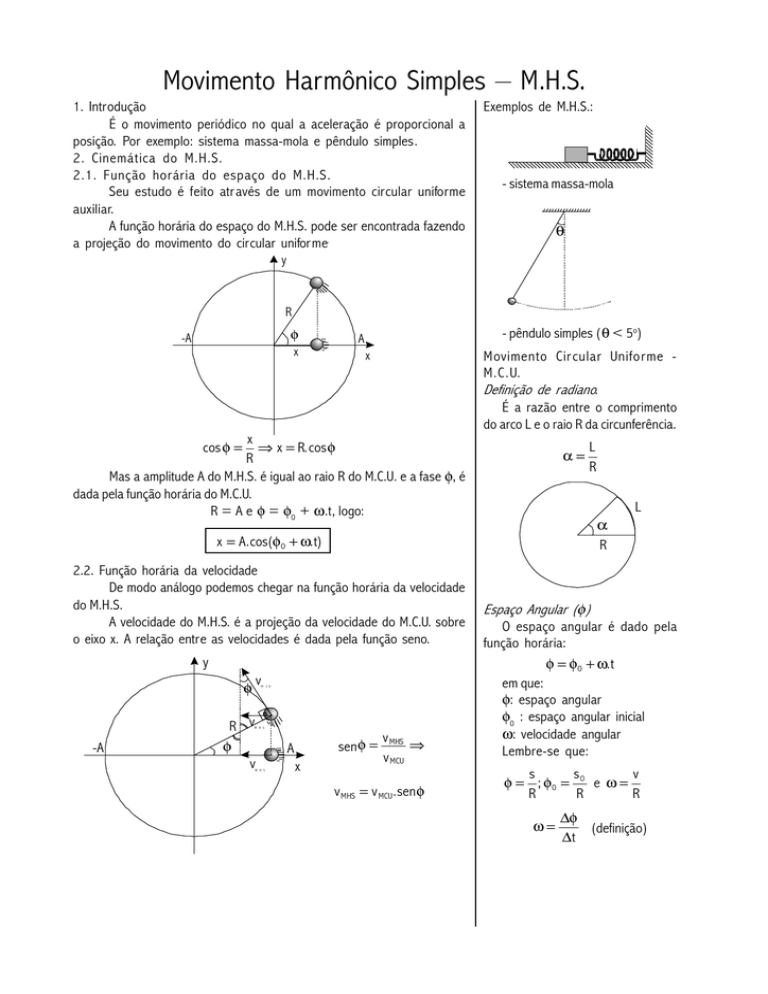
2.1. Função horária do espaço do M.H.S.
Seu estudo é feito através de um movimento circular uniforme
auxiliar.
A função horária do espaço do M.H.S. pode ser encontrada fazendo
a projeção do movimento do circular uniforme.
Exemplos de M.H.S.:
- sistema massa-mola
θ
y
R
-A
φ
x
A
- pêndulo simples (θ < 5o)
x
x
cos φ = ⇒ x = R. cos φ
R
Mas a amplitude A do M.H.S. é igual ao raio R do M.C.U. e a fase φ, é
dada pela função horária do M.C.U.
R = A e φ = φ0 + ω.t, logo:
Movimento Circular Uniforme M.C.U.
Definição de radiano.
É a razão entre o comprimento
do arco L e o raio R da circunferência.
α=
α
R
x = A. cos(φ0 + ω. t)
2.2. Função horária da velocidade
De modo análogo podemos chegar na função horária da velocidade
do M.H.S.
A velocidade do M.H.S. é a projeção da velocidade do M.C.U. sobre
o eixo x. A relação entre as velocidades é dada pela função seno.
y
v
φ
M CU
R v
φ
v
M H S
-A
M H S
A
x
sen φ =
v MHS
⇒
v MCU
v MHS = v MCU . sen φ
L
R
L
Espaço Angular (φ)
O espaço angular é dado pela
função horária:
φ = φ0 + ω. t
em que:
φ: espaço angular
φ0 : espaço angular inicial
ω: velocidade angular
Lembre-se que:
s
s
v
φ = ; φ0 = 0 e ω =
R
R
R
ω=
∆φ
(definição)
∆t
A aceleração centrípeta do M.C.U.
pode ser dada por duas relações:
a CP = ω .R ou a CP =
2
R
φ
a
v
R
2
- página 2 -
A velocidade linear do M.C.U. se relaciona com a velocidade
angular através da relação v=ω.R. Assim, a relação passa a ser:
v MHS = ω.R. senφ
Mais uma vez, lembrando que a amplitude do MHS é igual ao
raio do M.C.U., temos:
R = A e φ = φ0 + ω. t
v MHS = ω.A. sen(φ0 + ω.t)
ω
Note que não tem sentido mais a denominação velocidade
angular para um M.H.S., portanto ω será denominado de pulsação.
O sentido do M.C.U. auxiliar é anti-horário. Fazendo a correção
necessária devido a orientação do eixo x, temos:
v MHS = −ω. A. sen(φ0 + ω. t)
CP
Fase (φ
φ 0)
φ ) e fase inicial (φ
A fase inicial tem por referência a
posição inicial de um M.C.U. auxiliar
(imaginário). Por exemplo:
φ = 0 rad
2.3. Função horária da aceleração do M.H.S.
A aceleração do M.H.S. será a componente no eixo x da
aceleração centrípeta do M.C.U.. A relação entre as acelerações será
dada pela função co-seno.
y
0
a
R φ
a
φ
a
cos φ =
M C U
-A
M H S
M H S
-A
0
A
Neste caso imagina-se um M.C.U., cuja
posição angular inicial é φ0 = 0 radianos.
Como a posição do objeto que realiza o
M.H.S. é a projeção sobre o eixo x, então
tem-se que o móvel encontra-se na
posição x = A, movendo-se no sentido
contrário da orientação do eixo x.
φ = π/2 rad
0
-A
0
A
A
x
a MHS
⇒
a MCU
a MHS = aMCU . cos φ
Como a aceleração centrípeta é: a CP = ω2 .R
temos: a MHS = ω2 .R. cos φ
Corrigindo o sinal da aceleração devido a orientação do eixo x
e substituindo R = A e φ = φ0 + ω.t , temos a função:
a MHS = −ω . A .cos(φ0 + ω.t)
2
2.4. Equação fundamental do M.H.S.
Como a definição do M.H.S. é de um movimento no qual a
aceleração é proporcional a posição, temos:
a = k.x
comparando a função horária do espaço:
x = A. cos(φ0 + ω. t)
com a função horária da aceleração:
a MHS = −ω . A .cos(φ0 + ω.t)
chegamos a função fundamental do M.H.S.:
2
a MHS = −ω .x
2
em que: k = - ω2
- página 3 -
2.5. Diagramas horários do M.H.S.
Os diagramas das funções horárias do M.H.S. são gráficos de
funções trigonométricas. Funções como:
y = a sen (bx + c) + d
y = a cos (bx + c) + d
Vale lembrar que:
I - O termo a da função define a amplitude do gráfico:
2
y = cos x
y = 2 cos x
2
Neste caso imagina-se um M.C.U., cuja
posição angular inicial é φ0 = π/2
radianos. Como a posição do objeto que
realiza o M.H.S. é a projeção sobre o
eixo x, então tem-se que o móvel
encontra-se na posição x = 0,
movendo-se no sentido contrário da
orientação do eixo x.
φ0 = π rad
1
1
0
π
2
-1
3π
π
2
x
2π
0
π
2
-1
3π
π
2
x
2π
-A
-2
-2
0
A
II - O termo b da função define a período do gráfico, através da
relação T = 2π/b:
2
-1
-2
2
π
2
π
3π
2
x
2π
0
π
-1
3π
π
2
-1
2π
2
x
-2
III - O termo c da função define a fase inicial do gráfico:
y = cos x
2
1
0
Neste caso imagina-se um M.C.U., cuja
posição angular inicial é φ0 = π radianos.
Como a posição do objeto que realiza o
M.H.S. é a projeção sobre o eixo x, então
tem-se que o móvel encontra-se na
posição x = -A, movendo-se a favor do
sentido da orientação do eixo x.
φ0 = 3π/ 2 rad
1
1
0
y = cos 2x
π
y = cos (x + )
2
1
π
2
π
3π
2
2π
x
0
-π
2 -1
-2
π
2
π
3π
2
2π
x
-A
y = cos x
2
1
0
-1
-2
A
-2
IV - O termo d da função define a translação do gráfico no
eixo y (não será utilizada no estudo do M.H.S.):
2
0
2
y = cos x
y = cos x + 1
1
π
2
π
3π
2
2π
x
0
-1
-2
π
2
π
3π
2
2π
x
Neste caso imagina-se um M.C.U., cuja
posição angular inicial é φ0 = 3π/2
radianos. Como a posição do objeto que
realiza o M.H.S. é a projeção sobre o eixo
x, então tem-se que o móvel encontra-se
na posição x = 0, movendo-se a favor do
sentido da orientação do eixo x.
- página 4 -
2.6. Exercícios
1. (Unitau-95) Uma par tícula oscila ao longo do eixo x com movimento harmônico simples, dado por
x=3,0.cos(0,5πt + 3π/2), onde x é dado em cm e t em segundos. Nessas condições, pode-se afirmar que a amplitude,
a freqüência e a fase inicial valem, respectivamente:
a) 3,0cm, 4Hz, 3π/2rad
d) 3,0cm, 0,5Hz, 3π/2rad
b) 1,5cm, 4Hz, 3π/2rad
e) 3,0cm, 0,25Hz, 3π/2rad
c) 1,5cm, 4Hz, 270°
2. (UEL-95) Um movimento harmônico simples é descrito pela função x=0,050 cos(2πt+π), em unidades do
Sistema Internacional. Nesse movimento, a amplitude e o período, em unidades do Sistema Internacional,
valem, respectivamente,
a) 0,050 e 1,0
d) 2π e π
b) 0,050 e 0,50
e) 2,0 e 1,0
c) π e 2π
3. (Mackenzie 96) Uma partícula descreve um movimento harmônico simples segundo a equação:
x=0,3.cos(π/3+2.t), no S.I..
O módulo da máxima velocidade atingida por esta partícula é:
a) 0,3 m/s
d) 0,2 m/s
b) 0,1 m/s
e) π/3 m/s
c) 0,6 m/s
4. (UFRS 98) Uma massa M executa um movimento harmônico simples entre as posições x=-A e x=A, conforme
representa a figura. Qual das alternativas refere-se corretamente aos módulos e aos sentidos das grandezas
velocidade e aceleração da massa M na posição x=-A?
a) A velocidade é nula; a aceleração é nula.
b) A velocidade é máxima e aponta para a direita; a aceleração é nula.
c) A velocidade é nula; a aceleração é máxima e aponta para a direita.
d) A velocidade é nula; a aceleração é máxima e aponta para a esquerda.
e) A velocidade é máxima e aponta para a esquerda; a aceleração é máxima e aponta para a direita.
5. (Mackenzie 98) Um corpo efetua um movimento harmônico simples. Com relação a esse movimento, podemos
afirmar que:
a) a trajetória descrita pelo corpo é uma senóide.
b) o módulo da velocidade do corpo varia senoidalmente com o tempo.
c) o sentido da velocidade do corpo varia 4 vezes em cada período.
d) a aceleração do corpo tem módulo invariável.
e) o módulo da aceleração do corpo varia linearmente com o tempo.
6. (Mackenzie 98)Uma partícula realiza um M.H.S. (movimento harmônico simples), segundo a equação
x=0,2cos(π/2+πt/2), no S.I.. A partir da posição de elongação máxima, o menor tempo que esta par tícula
gastará para passar pela posição de equilíbrio é:
a) 0,5 s
d) 4 s
b) 1 s
e) 8 s
c) 2 s
7. (Fuvest-95) Uma caneta move-se ao longo do eixo y com um
movimento harmônico simples. Ela registra sobre uma fita de papel
que se move com velocidade de 10cm/s da direita para esquerda, o
gráfico representado na figura ao lado.
a) Determine a função y(x) que representa a curva mostrada no
gráfico.
b) Supondo que o instante t=0 corresponda à passagem da caneta
- página 5 -
pelo ponto x=0 e y=0, determine a função y(t) que representa seu
movimento.
c) Qual a freqüência, em hertz, do movimento da caneta?
8. (Fuvest-93) Enquanto uma folha de papel é puxada com velocidade
constante sobre uma mesa, uma caneta executa um movimento de
vai-e-vem, perpendicularmente à direção de deslocamento do papel,
deixando registrado na folha um traço em forma de senóide.
A figura ao lado representa um trecho AB do traço, bem como as
posições de alguns de seus pontos e os respectivos instantes.
Pede-se:
a) a velocidade de deslocamento da folha.
b) a razão das freqüências do movimento de vai-e-vem da caneta
entre os instantes 0 a 6s e 6 a 12s.
9. (Unicamp-91) Enquanto o ponto P se move sobre uma
circunferência, em movimento circular uniforme com velocidade
angular ω=2πrad/s, o ponto M (projeção de P sobre o eixo x) executa
um movimento harmônico simples entre os pontos A e A'.
a) Qual é a freqüência do MHS executado por M?
b) Determine o tempo necessário para o ponto M deslocar-se do
ponto B ao ponto C.
Nota: B e C são os pontos médios de AD e DA´ , respectivamente.
10. (Vunesp-91) A par tir do gráfico que ao lado onde estão
representadas as posições ocupadas por um móvel em função do
tempo, quando oscila sujeito a uma força do tipo -k.x (k constante),
determine:
a) a freqüência da amplitude do movimento.
b) os instantes, durante os três primeiros segundos, em que a
velocidade se anulou.
Respostas
6. B
8.
1. E
7.
a) 2,0 cm/s
2. A
a) y = 2,0 sen (π/2 . x)
b) 2
3. C
b) y = 2,0 sen (5,0 π t)
9.
4. C
c)
2,5
Hz
a) 1,0 Hz
5. B
3. Dinâmica do M.H.S.
O movimento harmônico simples é o movimento no qual a
aceleração é proporcional a posição. Por exemplo: sistema massamola e pêndulo simples. Isto é expresso através da equação
fundamental do M.H.S.:
a = k.x ou
a MHS = −ω .x , onde k = - ω
3.1. Sistema Massa-Mola
Um sistema conservativo formado por uma mola de constante
elástica k e um corpo de massa m. O corpo de massa m é posto a
oscilar entre as posições -A e A, quando sujeito a uma força elástica.
2
b) 1/6 s
10.
a) A = 0,10 m
f = 0,5 Hz
b) 0,5s; 1,5s e 2,5s
Aceleração do M.H.S.
Projeção da aceleração do M.C.U.
É a projeção da aceleração do
M.C.U. auxiliar sobre o eixo x.
y
2
a
R φ
a
φ
a
M CU
-A
M HS
M H S
A
x
comparando a função horária do
espaço: x = A. cos(φ0 + ω. t)
com a função horária da aceleração:
a MHS = −ω . A .cos(φ0 + ω.t)
chegamos a função fundamental do
M.H.S.:
2
2
a MHS = −ω .x , onde k = - ω2
Período do Sistema Massa-Mola.
O período do Sistema MassaMola não depende da inclinação θ do
plano inclinado.
- página 6 -
∆x
F
e lá s t
r
r r
r
FR = m.a e FElast = −k. x , portanto m.a = k.x (em módulo). Logo,
k
a = .x . Mas, da equção fundamental do M.H.S. temos que: a MHS = ω2 x
m
(em módulo).
Deste modo a pulsação do movimento harmônico é ω =
e o período do movimento harmônico é:
T = 2.π.
θ
Forças atuantes num pêndulo simples.
θ
φ
T
P
φ
-A
L
φ
Fr
a
Fr
x 0
a~x
k
m
m
k
3.2. Pêndulo Simples
Um objeto é preso a um fio ideal e posto a oscilar de modo
que θ o ângulo formado pelo fio ideal e um reta vertical não ultrapassa
o valor de 5 o.
Observa-se que a força resultante é dada pela componente do
peso na direção do movimento. Dessa forma, a intensidade da força
resultante é FR= P.sen φ.
Utilizando a aproximação, perfeitamente válida para ângulos
pequenos, medidos em radianos, sen φ ≈ φ, temos: FR ≈ P . φ.
Da definição de ângulo, em radianos, temos φ = x/L, a força
resultante pode ser escrita como:
x
L
Substituindo a segunda Lei de Newton, FR = m.a, deduz-se que
a aceleração do movimento é:
FR = P.
A
Tabela de ângulos e senos.
sen (α
α
α
α)
(graus) (radianos)
1
0,0175
0,0175
2
0,0349
0,0349
3
0,0524
0,0523
4
0,0698
0,0698
5
0,0873
0,0872
6
0,1047
0,1045
7
0,1222
0,1219
8
0,1396
0,1392
9
0,1571
0,1564
10
0,1745
0,1736
g
a = .x
L
Porém, por definição, o movimento harmônico simples é aquele
que tem sua aceleração proporcional a posição, ou seja: a MHS = ω2 x .
Deste modo a pulsação do movimento harmônico é:
g
L
E o período do pêndulo simples é:
ω=
T = 2.π.
L
g
- página 7 -
3.3 Exercícios
1. (Unicamp 92) Um corpo de massa m está preso em uma mola de
constante elástica k e em repouso no ponto O. O corpo é então puxado
até a posição A e depois solto. O atrito é desprezível. Sendo m=10kg,
k=40N/m, π=3,14, pede-se:
a) o período de oscilação do corpo;
b) o número de vezes que um observador, estacionário no ponto B, vê
o corpo passas por ele, durante um intervalo de 15,7 segundos.
2. (Uelondrina 96) Um corpo de massa m é preso à extremidade de
uma mola helicoidal que possui a outra extremidade fixa. O corpo é
afastado até o ponto A e, após ser abandonado, oscila entre os pontos
A e B.
Pode-se afirmar corretamente que a:
a) aceleração é nula no ponto 0.
d) força é nula nos pontos A e B.
b) a aceleração é nula nos pontos A e B.
e) força é máxima no ponto 0.
c) velocidade é nula no ponto 0.
3. (Mackenzie 97) Um corpo, preso a uma mola conforme figura ao
lado, executa na Terra um M. H. S. de freqüência 30Hz. Levando-se
esse sistema à Lua, onde a aceleração da gravidade é 1/6 da aceleração
da gravidade da Terra, a freqüência do M. H. S. descrito lá é:
a) 5 Hz
d) 60 Hz
b) 10 Hz
e) 180 Hz
c) 30 Hz
4. (Ufes 99) Dois blocos, 1 e 2, de massas m1 e m2, respectivamente,
comprimem uma mola, de constante elástica k, de uma distância x0 em
relação à sua posição de equilíbrio. O bloco 1 está preso à mola,
enquanto o bloco 2 é mantido em contato com o bloco 1, porém sem
estar preso a ele, por um agente externo, conforme mostra a figura. O
conjunto, inicialmente em repouso, em um dado momento, é deixado
livre por esse agente externo. Despreze todas as formas de dissipação de energia.
a) Que velocidade terá o bloco 2 quando perder contato com o bloco 1?
b) Depois que o bloco 2 perde o contato com o sistema massa-mola, esse sistema realiza um movimento
harmônico simples (MHS). Determine a freqüência angular e a amplitude desse MHS.
5. (Vunesp 91) Período de um pêndulo é o intervalo de tempo gasto numa oscilação completa. Um pêndulo
executa 10 oscilações completas em 9,0 segundos. Seu período é:
a) 0,9 segundos
d) 10,0 segundos
b) 1,1 segundos
e) 90,0 segundos
c) 9,0 segundos
6. (Fuvest-gv 92) Um trapezista abre as mãos, e larga a barra de um trapézio, ao passar pelo ponto mais baixo
da oscilação. Desprezando-se o atrito, podemos afirmar que o trapézio:
a) pára de oscilar.
d) não sofre alteração na sua freqüência
b) aumenta a amplitude de oscilação.
e) aumenta sua energia mecânica.
c) tem seu período de oscilação aumentado.
7. (Vunesp 96) Um estudante pretendia apresentar um relógio de
pêndulo numa feira de ciências com um mostrador de 5cm de altura,
como mostra a figura.Sabendo-se que, para pequenas oscilações, o
período de um pêndulo simples, é dado pela expressão
T = 2.π. (L / g) , pede-se:
a) Se o pêndulo for pendurado no posto O e tiver um período de 0,8
segundos, qual deveria ser a altura mínima do relógio? Para facilitar
- página 8 -
seus cálculos, admita g=(π2)m/s2.
b) Se o período do pêndulo fosse de 5 segundos, haveria algum inconveniente? Justifique.
8. (Ita 98) No início do século, Alber t Einstein propôs que forças
inerciais, como aquelas que aparecem em referenciais acelerados,
sejam equivalentes às forças gravitacionais. Considere um pêndulo
de comprimento L suspenso no teto de um vagão de trem em
movimento retilíneo com aceleração constante de módulo a, como
mostra a figura. Em relação a um observador no trem, o período de
pequenas oscilações do pêndulo ao redor da sua posição de equilíbrio
θ0 é:
a) 2.π. (L / g)
b) 2.π. [L /(g + a)]
c) 2.π. [L / (g2 − a 2 )]
d) 2.π. [L / (g + a )]
2
2
e) 2.π. (L / a.g )
9. (Ita 97) Um aluno do ITA levou um relógio, a pêndulo simples, de Santos, no litoral paulista, para São José dos
Campos, a 600m acima do nível do mar. O relógio marcava a hora correta em Santos, mas demonstra uma
pequena diferença em São José. Considerando a Terra como uma esfera com seu raio correspondendo ao nível
do mar, pode-se ESTIMAR que, em São José dos Campos, o relógio:
a) atrasa 8 min por dia.
b) atrasa 8 s por dia.
c) adianta 8 min por dia.
d) adianta 8 s por dia.
e) foi danificado, pois deveria fornecer o mesmo horário que em Santos.
10. (Ita 98) Um relógio de pêndulo simples é montado no pátio de um laboratório em Novosibirsk na Sibéria,
utilizando um fio de suspensão de coeficiente de dilatação 1x10-4 °C-1. O pêndulo é calibrado para marcar a hora
certa em um bonito dia de verão de 20°C. Em um dos menos agradáveis dias do inverno, com a temperatura a
-40°C, o relógio:
a) adianta 52 s por dia.
d) atrasa 26 s por dia.
b) adianta 26 s por dia.
e) atrasa 52 s por dia.
c) atrasa 3 s por dia.
11. (Mackenzie 98) Um pêndulo simples tem inicialmente um período T. Ao quadruplicarmos seu comprimento,
sua nova freqüência será:
a) 4T
b) 2T
c) 1/T
d) 1/2T
e) 1/4T
12. (Ita 96) Uma técnica muito empregada para medir o valor da aceleração da gravidade local é aquela que
utiliza um pêndulo simples. Para se obter a maior precisão no valor de g deve-se:
a) usar uma massa maior.
d) aumentar a amplitude das oscilações.
b) usar um comprimento menor para o fio.
e) fazer várias medidas com massas diferentes.
c) medir um número maior de períodos.
Respostas
7.
1.
a) 21 cm
a) 3,14 s
b) O inconveniente é que o relógio teria mais de 6 metros
b) 10
de altura. Impróprio para salas convencionais.
2. A
8. D
3. C
9. B
4.
10. B
a) V = x0 √[k/(m1+m2)]
11. D
b) ω = √(k/m1) e A = x0
12. C
5. A
6. D