(Microsoft PowerPoint - 04-Oscila\347\365es-Pendulo

29/08/2012
15.6
PÊNDULOS
Prof. Carlos Vieira,
com modificações
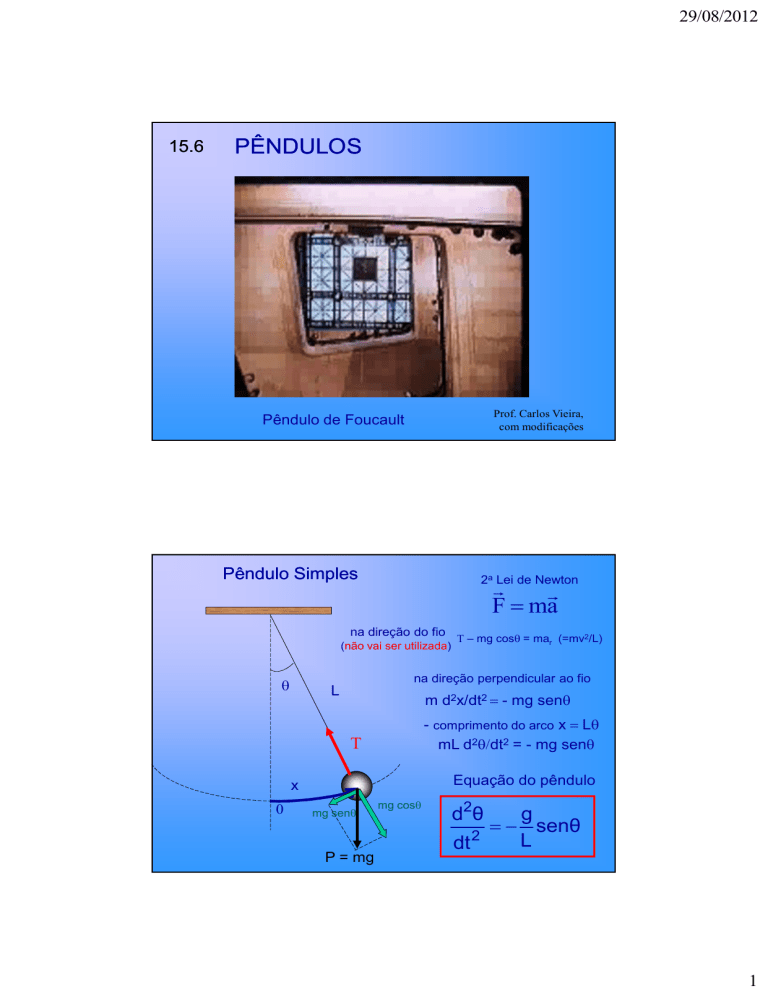
Pêndulo de Foucault
Pêndulo Simples
2a Lei de Newton
r
r
F = ma
na direção do fio
(não vai ser utilizada)
na direção perpendicular ao fio
θ
L
m d2x/dt2 = - mg senθ
- comprimento do arco x = Lθ
mL d2θ/dt2 = - mg senθ
Τ
Equação do pêndulo
x
0
Τ – mg cosθ = mar (=mv2/L)
mg senθ
P = mg
mg cosθ
d2 θ
g
=
−
senθ
L
dt 2
1
29/08/2012
Equação do pêndulo
d 2θ
dt 2
=−
Equação do
oscilador harmônico
g
senθ
L
d2x
2
+
ω
x =0
2
dt
Na aproximação de
pequenas oscilações,
quando senθ ≈ θ a
equação se escreve
d 2θ g
+ θ=0
2
L
dt
g
L
ω=
Período do
pêndulo
Τ = 2π
L
g
Comparação entre θ (em radiano) e senθ .
Observar que se pode considerar sen θ ≈ θ quando θ
for pequeno, isto é, θ até ≈20o ou θ ≈ 0,34 rad.
θ (graus)
0
30
60
90
1,5
θ
sen θ
1,0
0,5
0,0
0,0
0,5
θ (rad)
1,0
1,5
2
29/08/2012
O pêndulo, em pequenas oscilações, é um oscilador
harmônico cujo período T depende de g (aceleração
da gravidade) e do comprimento L do pêndulo.
L
g
Τ = 2π
As expressões do movimento são:
Posição angular
θ = θ0 cos(ωt + φ )
dθ
= −ω θ0 sen( ωt + φ )
dt
Velocidade angular
d 2θ
= −ω 2θ0 cos(ωt + φ )
2
dt
Aceleração angular
PÊNDULO FÍSICO
I - o momento de inércia em relação a O.
h – a distância entre o ponto de suspensão
e o centro de massa do corpo.
O
h
θ
Torque do peso em relação ao ponto O
I
h senθ
d 2θ
dt 2
d2 θ
dt
Mg
2
= − Mgh senθ
=−
Mgh
senθ
I
No caso de pequenas oscilações, isto é,
θ pequeno, sen θ ≈ θ.
d2θ
dt
2
= − ω2 θ
onde
ω=
Mgh
I
3
29/08/2012
15.7
Movimento Harmônico
Simples e
Movimento Circular Uniforme
Constante de fase
Amplitude
MHS
x (t ) = xm cos( ω t + φ )
Deslocamento
Frequência angular
Vamos ver que
o movimento oscilatório
harmônico simples
(MHS) é a projeção de
um movimento circular
uniforme (MCU) em um
eixo.
ESTUDO DO MOVIMENTO CIRCULAR
UNIFORME ( MCU )
4
29/08/2012
• Quando a esfera passa pela posição definida pelo ângulo
de fase φ, inicia-se a medida do tempo.
• À medida que o tempo evolui o ângulo de fase θ aumenta
com uma taxa ω.
t=0
r
φ
θ = ωt+φ
X
No MCU o corpo gira com uma velocidade angular ω
constante e realiza uma volta completa no tempo T.
T é o período do
movimento
T = 2π / ω
5
29/08/2012
CARACTERÍSTICAS DO MOVIMENTO CIRCULAR
Posição: definida pelo vetor r (que gira com velocidade angular
θ (rad) = arco / raio
s=θr
constante).
Velocidade: v é tangente à
circunferência e tem módulo
constante.
r r
v⊥r
v=ωr
A aceleração
dirigida para o
centro (centrípeta).
s
θ
r
a
v
x
a = v2 / r = ω2 r
6
29/08/2012
PROJEÇÃO DO MOVIMENTO CIRCULAR NO EIXO X
v
r
θ
O
x = r cos θ
X
A projeção está representada pelo ponto que se desloca ao
longo do eixo x. Na posição definida pela fase θ:
x = r cos θ.
A faixa azul representa a projeção da posição da
partícula no eixo x .
x(t) = xm cos (ω
ωt+ φο)
θ = ωt+ φο
xm
7
29/08/2012
Projeção do vetor velocidade do MCU.
v
θ
θ
O
vx = - v sen θ
-xm
xm
X
• vx é nula em x = ± xm e
• tem valor máximo vx max = ωxm em x=0.
-Vmax= -ωxm
Vx =0
Vx =0
-xm
xm
Vmax =+ ωxm
8
29/08/2012
Projeção do vetor aceleração do MCU.
a = ω2A
θ = ωt+φο
-A
O
ax = -a cos θ
A
X
ax = - ω2 A cos(ωt+φ )
A seta representa a componente x da aceleração.
ax = - ω2x = - ω2 A cos(ωt+φ).
A componente x da força é portanto
Fx = max = - m ω2 x,
isto é, Fx = - k x , sendo k = m ω2.
9
29/08/2012
As projeções da posição, velocidade e aceleração
são dadas pelas expressões:
Posição
x = xm cos ( ωt + φ)
Velocidade
vx = - ω xm sen ( ωt + φ)
Aceleração
ax = - ω2 xm cos( ωt + φ)
Como no Movimento Harmônico Simples !
− ω é a frequência angular (ω
ω2 = k/m),
− xm é a amplitude
− φ é a fase inicial ou constante de fase.
GENERALIZANDO
Quando uma força do tipo
F=-kx ,
sendo k constante, age sobre um corpo de
massa m, o movimento resultante é um
Movimento Harmônico Simples,
com frequência angular
ω=
k
m
10
29/08/2012
Projeção do
MCU
F = Kx
Circular.exe
Posição
de
equilíbrio
11