1. (Uerj 2015) Um esquiador, com 70kg de massa

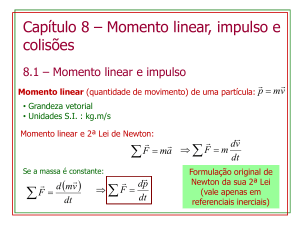
LISTA EXTRA – 3ª SÉRIE – IMPULSO, QUANT. DE MOVIMENTO E COLISÕES
1. (Uerj 2015) Um esquiador, com 70kg de massa, colide elasticamente contra uma
árvore a uma velocidade de 72km / h.
Calcule, em unidades do SI, o momento linear e a energia cinética do esquiador no
instante da colisão.
2. (Unesp 2015) O gol da conquista do tetracampeonato pela Alemanha na Copa do
Mundo de 2014 foi feito pelo jogador Götze. Nessa jogada, ele recebeu um cruzamento,
matou a bola no peito, amortecendo-a, e chutou de esquerda para fazer o gol. Considere
que, imediatamente antes de tocar o jogador, a bola tinha velocidade de módulo
V1  8 m / s
em uma direção perpendicular ao seu peito e que, imediatamente depois de
tocar o jogador, sua velocidade manteve-se perpendicular ao peito do jogador, porém
com módulo V2  0,6 m / s e em sentido contrário.
Admita que, nessa jogada, a bola ficou em contato com o peito do jogador por 0,2 s e
que, nesse intervalo de tempo, a intensidade da força resultante (FR ), que atuou sobre
ela, variou em função do tempo, conforme o gráfico.
Página 1 de 16
LISTA EXTRA – 3ª SÉRIE – IMPULSO, QUANT. DE MOVIMENTO E COLISÕES
Considerando a massa da bola igual a 0,4 kg, é correto afirmar que, nessa jogada, o
módulo da força resultante máxima que atuou sobre a bola, indicada no gráfico por
Fmáx , é igual, em newtons, a
a) 68,8.
b) 34,4.
c) 59,2.
d) 26,4.
e) 88,8.
3. (Uerj 2015) Admita uma colisão frontal totalmente inelástica entre um objeto que se
move com velocidade inicial v 0 e outro objeto inicialmente em repouso, ambos com
mesma massa.
Nessa situação, a velocidade com a qual os dois objetos se movem após a colisão
equivale a:
a)
v0
2
b)
v0
4
c) 2v0
d) 4v0
4. (Fuvest 2015) Um trabalhador de massa m está em pé, em repouso, sobre uma
plataforma de massa M. O conjunto se move, sem atrito, sobre trilhos horizontais e
retilíneos, com velocidade de módulo constante v. Num certo instante, o trabalhador
começa a caminhar sobre a plataforma e permanece com velocidade de módulo v, em
relação a ela, e com sentido oposto ao do movimento dela em relação aos trilhos. Nessa
situação, o módulo da velocidade da plataforma em relação aos trilhos é
a)  2 m  M v / m  M
b)  2 m  M v / M
c)  2 m  M v / m
d) M  m v / M
Página 2 de 16
LISTA EXTRA – 3ª SÉRIE – IMPULSO, QUANT. DE MOVIMENTO E COLISÕES
e) m  M v / M  m
5. (Enem 2014)
Para entender os movimentos dos corpos, Galileu discutiu o
movimento de uma esfera de metal em dois planos inclinados sem atritos e com a
possibilidade de se alterarem os ângulos de inclinação, conforme mostra a figura. Na
descrição do experimento, quando a esfera de metal é abandonada para descer um plano
inclinado de um determinado nível, ela sempre atinge, no plano ascendente, no máximo,
um nível igual àquele em que foi abandonada.
Se o ângulo de inclinação do plano de subida for reduzido a zero, a esfera
a) manterá sua velocidade constante, pois o impulso resultante sobre ela será nulo.
b) manterá sua velocidade constante, pois o impulso da descida continuará a empurrá-la.
c) diminuirá gradativamente a sua velocidade, pois não haverá mais impulso para
empurrá-la.
d) diminuirá gradativamente a sua velocidade, pois o impulso resultante será contrário
ao seu movimento.
e) aumentará gradativamente a sua velocidade, pois não haverá nenhum impulso
contrário ao seu movimento.
6. (Ufrgs 2014)
Um objeto de massa igual a 2 kg move-se em linha reta com
velocidade constante de 4 m / s. A partir de um certo instante, uma força de módulo
igual a 2N é exercida por 6 s sobre o objeto, na mesma direção de seu movimento. Em
seguida, o objeto colide frontalmente com um obstáculo e tem seu movimento invertido,
afastando-se com velocidade de 3 m / s.
O módulo do impulso exercido pelo obstáculo e a variação da energia cinética do
objeto, durante a colisão, foram, respectivamente,
Página 3 de 16
LISTA EXTRA – 3ª SÉRIE – IMPULSO, QUANT. DE MOVIMENTO E COLISÕES
a) 26 Ns e -91 J.
b) 14 Ns e -91 J.
c) 26 Ns e -7 J.
d) 14 Ns e -7 J.
e) 7 Ns e -7 J.
7. (G1 - cftmg 2014) Um objeto, deslocando-se com uma quantidade de movimento de
20 kg  m / s,
colide com um obstáculo durante 0,010 s e para. O valor médio da força
impulsiva que atua nesse objeto é, em newtons,
a) 1,0  101.
b) 2,0  101.
c) 1,0  103.
d) 2,0  103.
8. (Espcex (Aman) 2014) Um bloco de massa M=180 g está sobre urna superfície
horizontal sem atrito, e prende-se a extremidade de uma mola ideal de massa
desprezível e constante elástica igual a 2  103 N / m. A outra extremidade da mola está
presa a um suporte fixo, conforme mostra o desenho. Inicialmente o bloco se encontra
em repouso e a mola no seu comprimento natural, Isto é, sem deformação.
Um projétil de massa m=20 g é disparado horizontalmente contra o bloco, que é de fácil
penetração. Ele atinge o bloco no centro de sua face, com velocidade de v=200 m/s.
Devido ao choque, o projétil aloja-se no interior do bloco. Desprezando a resistência do
ar, a compressão máxima da mola é de:
a) 10,0 cm
b) 12,0 cm
c) 15,0 cm
Página 4 de 16
LISTA EXTRA – 3ª SÉRIE – IMPULSO, QUANT. DE MOVIMENTO E COLISÕES
d) 20,0 cm
e) 30,0 cm
9. (Ufsm 2014) A hipótese mais aceita nos meios científicos atribui a grande extinção
da fauna terrestre, ocorrida há aproximadamente 65 milhões de anos, à colisão de um
corpo celeste de grandes dimensões, possivelmente um cometa, com a superfície da
Terra. Esse bólido foi absorvido pela Terra e o que se seguiu foi um súbito desequilíbrio
ambiental, que incluiu obstrução da passagem da luz solar, maremotos e violentas
erupções vulcânicas.
A respeito das propriedades desse tipo de colisão, complete as lacunas na afirmação a
seguir.
Trata-se de um exemplo de choque perfeitamente __________, em que o momento
linear do sistema cometa-Terra __________ conservado. Nesse evento, ocorre
__________ da energia mecânica.
Assinale a sequência correta.
a) inelástico – é – conservação
b) elástico – não é – conservação
c) elástico – não é – dissipação
d) inelástico – não é – conservação
e) inelástico – é – dissipação
10. (Enem 2014) O pêndulo de Newton pode ser constituído por cinco pêndulos
idênticos suspensos em um mesmo suporte. Em um dado instante, as esferas de três
pêndulos são deslocadas para a esquerda e liberadas, deslocando-se para a direita e
colidindo elasticamente com as outras duas esferas, que inicialmente estavam paradas.
Página 5 de 16
LISTA EXTRA – 3ª SÉRIE – IMPULSO, QUANT. DE MOVIMENTO E COLISÕES
O movimento dos pêndulos após a primeira colisão está representado em:
a)
b)
c)
d)
e)
11. (Ufpe 2013) Uma partícula de massa 0,2 kg move-se ao longo do eixo x. No
instante t=0, a sua velocidade tem módulo 10 m/s ao longo do sentido positivo do eixo.
A figura a seguir ilustra o impulso da força resultante na direção x agindo sobre a
partícula. Qual o módulo da quantidade de movimento da partícula (em kg.m/s) no
instante t=15s?
Página 6 de 16
LISTA EXTRA – 3ª SÉRIE – IMPULSO, QUANT. DE MOVIMENTO E COLISÕES
12. (Upe 2013) “Curiosity pousa com sucesso em Marte”. Essa foi a manchete em
vários meios de comunicação na madrugada do dia 6 de agosto de 2012. O robô da Nasa
chamado Curiosity foi destinado a estudar propriedades do planeta Marte. Após uma
viagem de aproximadamente 9 meses, o Curiosity chegou a Marte. Ao entrar na
atmosfera do planeta, o robô continuava ligado a pequenos foguetes que foram usados
para desacelerá-lo. Segundos antes da chegada ao solo, os foguetes foram
desconectados e se afastaram para bem longe. A figura ilustra o sistema Curiosity +
foguetes.
A massa dos foguetes varia continuamente, enquanto eles queimam combustível e
produzem a exaustão dos gases. A propulsão dos foguetes que fizeram desacelerar o
Curiosity é um exemplo notável da
a) Lei da Inércia.
b) Lei de Kepler.
c) Conservação da Energia.
d) Conservação da Quantidade de Movimento.
e) Lei da Gravitação Universal.
Página 7 de 16
LISTA EXTRA – 3ª SÉRIE – IMPULSO, QUANT. DE MOVIMENTO E COLISÕES
13. (Ibmecrj 2013) Dois blocos maciços estão separados um do outro por uma mola
comprimida e mantidos presos comprimindo essa mola. Em certo instante, os dois
blocos são soltos da mola e passam a se movimentar em direções opostas. Sabendo-se
que a massa do bloco 1 é o triplo da massa do bloco 2, isto é m1 = 3m2, qual a relação
entre as velocidades v1 e v2 dos blocos 1 e 2, respectivamente, logo após perderem
contato com a mola?
a) v1 = - v2/4
b) v1 = -v2/3
c) v1 = v2
d) v1 = 3v2
e) v1 = 4v2
14. (Pucrj 2013) Uma massinha de 0,3 kg é lançada horizontalmente com velocidade de
5,0 m/s contra um bloco de 2,7 kg que se encontra em repouso sobre uma superfície
sem atrito. Após a colisão, a massinha se adere ao bloco.
Determine a velocidade final do conjunto massinha-bloco em m/s imediatamente após a
colisão.
a) 2,8
b) 2,5
c) 0,6
d) 0,5
e) 0,2
15. (Pucrj 2013) Na figura abaixo, o bloco 1, de massa m1 = 1,0 kg, havendo partido do
repouso, alcançou uma velocidade de 10 m/s após descer uma distância d no plano
inclinado de 30°. Ele então colide com o bloco 2, inicialmente em repouso, de massa m2
= 3,0 kg. O bloco 2 adquire uma velocidade de 4,0 m/s após a colisão e segue a
Página 8 de 16
LISTA EXTRA – 3ª SÉRIE – IMPULSO, QUANT. DE MOVIMENTO E COLISÕES
trajetória semicircular mostrada, cujo raio é de 0,6 m. Em todo o percurso, não há atrito
entre a superfície e os blocos. Considere g = 10 m/s2.
a) Ao longo da trajetória no plano inclinado, faça o diagrama de corpo livre do bloco 1 e
encontre o módulo da força normal sobre ele.
b) Determine a distância d percorrida pelo bloco 1 ao longo da rampa.
c) Determine a velocidade do bloco 1 após colidir com o bloco 2.
d) Ache o módulo da força normal sobre o bloco 2 no ponto mais alto da trajetória
semicircular.
16. (Uerj 2012) Observe a tabela abaixo, que apresenta as massas de alguns corpos em
movimento uniforme.
Corpos
leopardo
Massa Velocidade
(kg)
(km/h)
120
60
automóvel 1100
70
caminhão
20
3600
Admita que um cofre de massa igual a 300 kg cai, a partir do repouso e em queda livre
de uma altura de 5 m. Considere Q1 , Q2 , Q3 e Q4 , respectivamente, as quantidades de
movimento do leopardo, do automóvel, do caminhão e do cofre ao atingir o solo. As
magnitudes dessas grandezas obedecem relação indicada em:
a) Q1  Q4  Q2  Q3
b) Q4  Q1  Q2  Q3
c) Q1  Q4  Q3  Q2
d) Q4  Q1  Q3  Q2
Página 9 de 16
LISTA EXTRA – 3ª SÉRIE – IMPULSO, QUANT. DE MOVIMENTO E COLISÕES
Gabarito:
Resposta da questão 1:
Dados: m  70 kg; v  72 km/h  20 m/s.

p  m v  70  20  p  1.400 kg  m/s.


2
m v 2 70  20 

EC 

 EC  14.000 J.


2
2
Resposta da questão 2:
[B]
Orientando a trajetória no sentido da velocidade de chegada, V1  8 m/s e V2   0,6 m/s.
Durante a colisão, o impulso da força resultante é numericamente igual à área entre a
linha do gráfico e o eixo dos tempos. Assim, aplicando o teorema do impulso:
v
v
IFv  ΔQ
Fmáx Δt

2
v
2 m Δv
2  0,4  0,6  8
v
 m Δv  Fmáx 


Δt
0,2
Fmáx  34,4 N.
Resposta da questão 3:
[A]
Pela conservação da quantidade de movimento:
m v0  2 m v

v
v 0
2
Resposta da questão 4:
[A]
Página 10 de 16
LISTA EXTRA – 3ª SÉRIE – IMPULSO, QUANT. DE MOVIMENTO E COLISÕES
A figura ilustra a situação, mostrando as velocidades do trabalhador e da plataforma, em
relação ao referencial fixo no solo nas situações (I) e (II).
Pela conservação da Quantidade de Movimento:
 m  M v  M v '  m  v '  v   m v  M v  M v '  m v '  m v
2 m v  M v   M  m  v '   2 m  M v   M  m  v ' 
Q(I)  Q(II) 
v' 
2 m
M
 M v
 m

.
Resposta da questão 5:
[A]
Se o ângulo de inclinação do plano de subida for reduzido à zero, a esfera passa a se
deslocar num plano horizontal. Sendo desprezíveis as forças dissipativas, a resultante
das forças sobre ela é nula, portanto o impulso da resultante também é nulo, ocorrendo
conservação da quantidade de movimento. Então, por inércia, a velocidade se mantém
constante.
Página 11 de 16
LISTA EXTRA – 3ª SÉRIE – IMPULSO, QUANT. DE MOVIMENTO E COLISÕES
Resposta da questão 6:
[A]
Dados: v0 = 4 m/s; F = 2 N; m = 2 kg; v' = -3 m/s.
Aplicando o teorema do impulso ao processo de aceleração:
m Δv  F Δt  Δv 
F Δt
2 6
 v4 
 v  10 m/s.
m
2
Aplicando o teorema do impulso à colisão:
I  m Δv '
 I  m v ' v  I  2 3  10  I  26 N  s.
Calculando a variação da energia cinética na colisão:
ΔEC 

m v'2 m v 2
m 2 2


v'  v
2
2
2




2 3
3  102  9  100 
2
ΔEC  91 J.
Resposta da questão 7:
[D]
Supondo que a mencionada força seja a resultante, aplicando o teorema do impulso,
vem:
I Fv  ΔQ  F Δt  ΔQ  F 
ΔQ
20
=

Δt 0,01
F  2  103 N.
Resposta da questão 8:
[D]
Dados: M  180g  18  10–2 kg; m  20g  2  10–2 kg; k  2  10–3 N / m; v  200m / s.
Página 12 de 16
LISTA EXTRA – 3ª SÉRIE – IMPULSO, QUANT. DE MOVIMENTO E COLISÕES
Pela conservação da quantidade de movimento calculamos a velocidade do sistema (vs)
depois da colisão:
M  m  v s  m v
Qdepois
 Qantes

sist
sist
 200 v s  20  200  v s  20 m/s.
Depois da colisão, o sistema é conservativo. Pela conservação da energia mecânica
calculamos a máxima deformação (x) sofrida pela mola.
inicial
final
EMec
 EMec
x  20 

M  m v 2s
2
18  2   102
2  103
 20 

k x2
2
20  102
2  103
 x  vs
 20  104
Mm
k

 x  20  10 2 m 
x  20 cm.
Resposta da questão 9:
[E]
Trata-se de um exemplo de choque perfeitamente inelástico, pois o bólido ficou
incrustado na Terra. Sendo um sistema mecanicamente isolado, o momento linear
(quantidade de movimento) é conservado. Nesse evento, ocorre dissipação da energia
mecânica.
Resposta da questão 10:
[C]
Como se trata de sistema mecanicamente isolado, ocorre conservação da quantidade de
movimento.
Qfinal  Qincial

Qfinal  3 mv.
Portanto, após as colisões, devemos ter três esferas bolas com velocidade v como
mostra a alternativa [C].
Podemos também pensar da seguinte maneira: as esferas têm massas iguais e os
Página 13 de 16
LISTA EXTRA – 3ª SÉRIE – IMPULSO, QUANT. DE MOVIMENTO E COLISÕES
choques são frontais e praticamente elásticos. Assim, a cada choque, uma esfera para,
passando sua velocidade para a seguinte. Enumerando as esferas da esquerda para a
direita de 1 a 5, temos:
– A esfera 3 choca-se com a 4, que se choca com a 5. As esferas 3 e 4 param e a 5 sai
com velocidade v;
– A esfera 2 choca-se com a 3, que se choca com a 4. As esferas 2 e 3 param e a 4 sai
com velocidade v;
– A esfera 1 choca-se com a 2, que se choca com a 3. As esferas 1 e 2 param e a 3 sai
com velocidade v.
Resposta da questão 11:
Do gráfico, concluímos que o impulso exercido pela força resultante de 0 a 15 s é -20
kgm/s.
Do Teorema Impulso:
IRv  Qf  Qi  IRv  Qf  m v0 
 20  Qf  0,2  10  Qf  20  2  18 
Qf  18 kg  m/s.
Resposta da questão 12:
[D]
Para pequenos intervalos de tempo, o sistema formado pelo robô e pelos gases pode ser
considerado isolado de forças externas e, portanto, há conservação da quantidade de
movimento.
Resposta da questão 13:
[B]
Como o sistema é isolado de forças o momento linear total se conserva.
Página 14 de 16
LISTA EXTRA – 3ª SÉRIE – IMPULSO, QUANT. DE MOVIMENTO E COLISÕES
r
r
r
r
Q  Q0  m1v1  m2 v 2  0
r
r
r
r
r
r
v2
3m2 v1  m2 v 2  0  3v1  v 2  v1  
3
Resposta da questão 14:
[D]
O sistema é isolado. Há conservação da quantidade de movimento total do sistema.
r
r
Q  Q0  M  m.V  mV0  3V  0,3x5  V  0,5 m/s
Resposta da questão 15:
Em toda a questão o atrito será desprezado
a) Observando a figura abaixo podemos concluir que N  Pcos30  10
3
 5 3N.
2
b) Pela conservação da energia.
mgdsen30 
1
mV 2  10xdx0,5  0,5x102  d  10 m
2
c) Pela conservação da quantidade de movimento na colisão, vem:
m1V1  m2 V2  m1  V0 1  m2  V0 2
1xV1  3x4  1x10  3x0  V1  10  12  2,0m / s
d) As figuras abaixo mostram as posições inicial e final do bloco 2 e as forças que agem
sobre ele no topo da lombada.
Página 15 de 16
LISTA EXTRA – 3ª SÉRIE – IMPULSO, QUANT. DE MOVIMENTO E COLISÕES
Podemos determinar V pela Conservação da energia.
1
1
mV 2  mgH  mV02  V 2  2gH  V02
2
2
1 2
1
V  10x0,6  x42  V 2  4
2
2
A força centrípeta no topo da trajetória vale:
P N  m
V2
4
 30  N  3x
 30  N  20  N  10N
R
0,6
Resposta da questão 16:
[C]
Calculemos a velocidade do cofre ao atingir o solo, considerando g  10 m/s2 .
Aplicando Torricelli:
v2  v02  2gh  v  2  10  5  v  10 m / s  36 km / h.
Inserindo esses dados na tabela e calculando as quantidades de movimento.
Corpos
Massa Velocidade Quantidade de movimento
(kg)
(km/h)
(kg.km/h)
120
60
Q1 = 7.200
automóvel 1100
70
Q2 = 77.000
caminhão
3600
20
Q3 = 72.000
cofre
300
36
Q4 = 10.800
leopardo
Analisando os valores obtidos, constatamos que: Q1  Q4  Q3  Q2.
Página 16 de 16