Solução

www.fisicaexe.com.br
Uma rã de massa m está parada no extremo de uma tábua de massa M e comprimento
L. A tábua está flutuando na superfície de um lago. A rã salta, formando um ângulo α com a
horizontal na direção da tábua. Qual deve ser a velocidade inicial da rã para que depois do
salto ela esteja no outro extremo da tábua?
Dados do problema
•
•
•
•
massa da rã:
massa da tábua:
comprimento da tábua:
ângulo entre o salto da rã e a tábua:
m;
M;
L;
α.
Esquema do problema
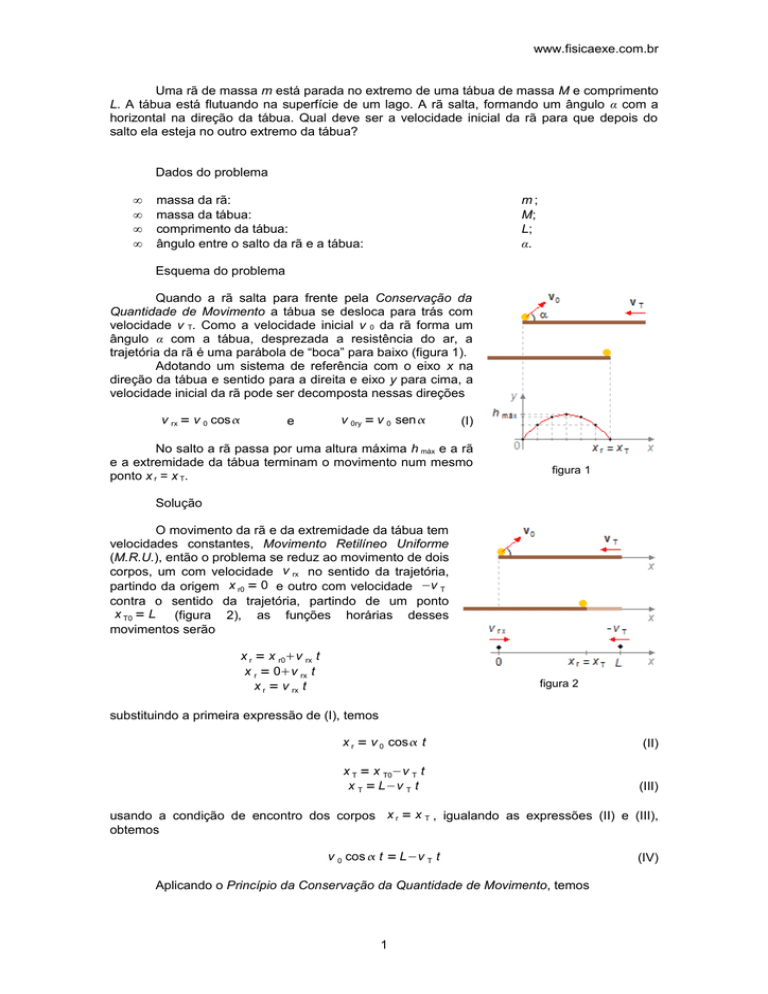
Quando a rã salta para frente pela Conservação da
Quantidade de Movimento a tábua se desloca para trás com
velocidade v T. Como a velocidade inicial v 0 da rã forma um
ângulo α com a tábua, desprezada a resistência do ar, a
trajetória da rã é uma parábola de “boca” para baixo (figura 1).
Adotando um sistema de referência com o eixo x na
direção da tábua e sentido para a direita e eixo y para cima, a
velocidade inicial da rã pode ser decomposta nessas direções
v rx = v 0 cos 
e
v 0ry = v 0 sen 
(I)
No salto a rã passa por uma altura máxima h máx e a rã
e a extremidade da tábua terminam o movimento num mesmo
ponto x r = x T.
figura 1
Solução
O movimento da rã e da extremidade da tábua tem
velocidades constantes, Movimento Retilíneo Uniforme
(M.R.U.), então o problema se reduz ao movimento de dois
corpos, um com velocidade v rx no sentido da trajetória,
partindo da origem x r0 = 0 e outro com velocidade −v T
contra o sentido da trajetória, partindo de um ponto
x T0 = L (figura 2), as funções horárias desses
movimentos serão
x r = x r0v rx t
x r = 0v rx t
x r = v rx t
figura 2
substituindo a primeira expressão de (I), temos
x r = v 0 cos t
(II)
x T = x T0−v T t
x T = L−v T t
(III)
usando a condição de encontro dos corpos x r = x T , igualando as expressões (II) e (III),
obtemos
v 0 cos  t = L−v T t
Aplicando o Princípio da Conservação da Quantidade de Movimento, temos
1
(IV)
www.fisicaexe.com.br
Qi =Qf
Q ri Q Ti = Q rfQ Tf
m v rxiM v Ti = m v rxf M v Tf
inicialmente a tábua está em repouso (v Ti = 0) e a componente da velocidade da rã na direção
da tábua é dada pela primeira das expressões em (I) v rxi = v rx, no final do salto a rã para na
extremidade da tábua (v rxf = 0) e a tábua está se movendo com velocidade v Tf = v T
m v 0 cos M .0 = m .0M v T
m v 0 cos  = M v T
M
vT=
v cos
m 0
(V)
O intervalo de tempo que a rã leva para dar o salto é o mesmo intervalo que a
extremidade da tábua leva para chegar onde a rã termina o salto, este também é o mesmo
intervalo de tempo que a rã leva para subir, atingir a altura máxima e descer (figura 1).
Adotando g para a aceleração da gravidade e usando a segunda expressão de (I) para
a componente da velocidade na direção y, o movimento da rã nesta direção está sob a ação da
aceleração da gravidade, esta em Movimento Retilíneo Uniformemente Variado (M.R.U.V.), a
função da velocidade nesta direção será
v ry = v 0ry−g t
v ry = v 0 sen − g t
quando a rã atinge a altura máxima a componente da velocidade na direção y se anula (v ry = 0)
por um instante, inverte o sinal, e começa a cair, assim o tempo para atingir a altura máxima
será
0 = v 0 sen −g t h
v 0 sen 
th =
g
o intervalo de tempo para a rã subir e descer será o dobro deste valor
t=2
v 0 sen 
g
(VI)
substituindo as expressões (V) e (VI) em (IV), obtemos
v 0 sen 
v 0 sen
M
= L− v 0 cos  2
g
m
g
2
2
2 v 0 cos  sen 
2
v
cos
sen

M
0
= L−
g
m
g
v 0 cos  2
lembrando que sen 2  = 2 cos  sen  e multiplicando toda a expressão por g, temos
2
2
v 0 sen 2 
m v 0 sen 2
= L−
g
M
g
2
2
v 0 sen 2 
v
sen
2
m 0
g = g L−
g
g
M
g
m 2
2
v 0 sen 2  = g L− v 0 sen 2 
M
m 2
2
v 0 sen 2  v 0 sen 2  = g L
M
m
2
v 0 sen 2  1
= gL
M


2
. g 
www.fisicaexe.com.br


M m
=gL
M
g LM
2
v0=
sen 2  M m 
v 20 sen 2 
v 0=

gLM
sen 2   M m 
3