7º Aula: Análise de Sinais no Domínio da Freqüência

Avaliação da Qualidade da Energia Elétrica
S.M.Deckmann e J.A.Pomilio
3. Análise de Sinais no Domínio da Frequência
Para existir um mapeamento entre fenômenos analisados nos domínios do tempo e da
frequência, o comportamento da grandeza no domínio do tempo deve ser periódico, ou seja, repetir-se
em intervalos iguais a T, sendo T o período de tempo que contém um ciclo do sinal de frequência f.
1
Com isso se estabelece a regra básica de mapeamento entre os dois domínios:
f  . Um ponto
T
importante é identificar em quais condições se torna mais conveniente analisar um sinal no domínio
da frequência.
3.1 Representação no Domínio do Tempo
No domínio do tempo precisa-se definir explicitamente a função e os parâmetros que a
caracterizam, por exemplo:
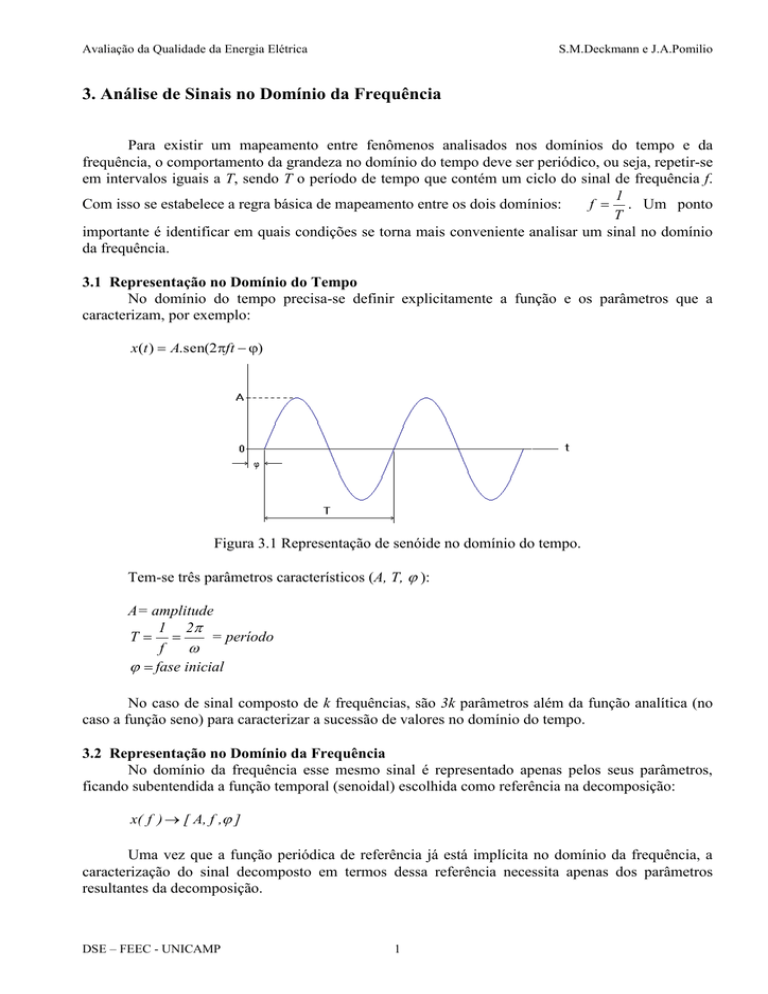
x(t )  A.sen(2ft  )
Figura 3.1 Representação de senóide no domínio do tempo.
Tem-se três parâmetros característicos (A, T,  ):
A= amplitude
1 2
T 
= período
f

  fase inicial
No caso de sinal composto de k frequências, são 3k parâmetros além da função analítica (no
caso a função seno) para caracterizar a sucessão de valores no domínio do tempo.
3.2 Representação no Domínio da Frequência
No domínio da frequência esse mesmo sinal é representado apenas pelos seus parâmetros,
ficando subentendida a função temporal (senoidal) escolhida como referência na decomposição:
x( f )  [ A, f , ]
Uma vez que a função periódica de referência já está implícita no domínio da frequência, a
caracterização do sinal decomposto em termos dessa referência necessita apenas dos parâmetros
resultantes da decomposição.
DSE – FEEC - UNICAMP
1
Avaliação da Qualidade da Energia Elétrica
S.M.Deckmann e J.A.Pomilio
Amplitude
A
Fase
f
0
0
f

Figura 3.2 Representação de senóide no domínio da frequência.
Nem todas as funções definidas no domínio do tempo apresentam período. Por exemplo, a
função:
f ( t )  cos 1t  cos 2t
será periódica apenas se a relação entre as frequências angulares for um número racional:
1 m
 , para n e m inteiros.
2 n
Desta forma, a função abaixo não é periódica, embora esteja descrita no domínio do tempo e
seja composta por dois sinais periódicos.
f ( t )  cos 10t  cos( 10   )t
Figura 3.3 Forma de onda não periódica.
3.3 Representação de Sinais Periódicos
Um sinal periódico qualquer pode ser expresso como série de senos e cossenos. Por exemplo,
a função:
1
1
1
f 1 ( t )  sen  1 t  sen 2 1 t  sen 3 1 t  sen 4 1 t  ...
2
3
4

produz uma onda dente de serra, com valor de pico .
2
4
1
1

Por outro lado a função f 2 ( t )  cos  1 t  cos 3 1 t  cos 5 1 t  ... produz uma onda

3
5

quadrada de amplitude unitária.
DSE – FEEC - UNICAMP
2
Avaliação da Qualidade da Energia Elétrica
S.M.Deckmann e J.A.Pomilio
a)
b)
Figura 3.4 a) Soma dos primeiros cinco termos da série da onda dente de serra.
b) Soma dos primeiros cinco termos da série de uma onda quadrada.
A
4
f3( t ) 

função
correspondente
a
uma
1
1


 sen  1 t  9 sen 3 1 t  25 sen 5 1 t  ...
onda
triangular
é
dada
por
Figura 3.5 Primeiros 3 termos da série da onda triangular.
Os três exemplos mostram algumas propriedades gerais importantes da denominada Série de
Fourier ou, como é também chamada, série harmônica (pois as componentes possuem frequências
múltiplas inteiras da fundamental):

1 - As séries são formadas por múltiplos inteiros da frequência fundamental ( f 1  1 ) . As
2
frequências múltiplas são chamadas harmônicas (fh = h.f1, h = 2,3,4...).
2 - Se a função é par [f(t) = f(-t)], a série contém apenas termos em cosseno; se a função for ímpar
[f(t) = -f(-t)], contém apenas termos em seno.
3 - Se a função apresentar simetria de meia onda [ f (t )   f (t  T2 )] a série não contém
harmônicas pares.
4 – Se, no tempo, a função tiver descontinuidades, aparece o efeito Gibbs nos pontos de derivada
infinita, devido à impossibilidade de reproduzir esse efeito pela soma de termos finitos em
frequência.
DSE – FEEC - UNICAMP
3
Avaliação da Qualidade da Energia Elétrica
S.M.Deckmann e J.A.Pomilio
3.4 Como aplicar a Análise de Fourier
As propriedades anteriores ajudam a simplificar a análise qualitativa, porém é necessário um
procedimento para decompor a função em sua série harmônica. A série de Fourier é uma
decomposição do sinal periódico em uma somatório de funções cosseno e seno:


2
f (t )  A0   Ah cos(h1t )   Bh sen(h 1t ) ,
sendo  1 
T
h 1
h 1
A análise pela série de Fourier, no domínio da frequência, para sinais periódicos, resume-se a
determinar os valores dos coeficientes A e B da série, uma vez que se conhece o período T da função
de referência. Sabendo que as funções cosseno e seno são ortogonais, a decomposição de Fourier
pode ser vista como uma operação de projeção em base de sinais ortogonais:
fe
f1
fe
c12.f2
f2
Figura 3.6 Decomposição ortogonal do sinal f1.
C12 é a medida da projeção ortogonal da função f1 sobre a função f2. Para determinar C12
sobre um intervalo de tempo [ta,tb] pode-se utilizar a técnica de erro quadrático médio mínimo para
a função de erro fe , dada por
fe (t)= f1 (t)- C12. f2 (t), ou seja,  f1 (t)= fe (t)+ C12. f2 (t)
eab 
O erro quadrático médio no intervalo será, portanto:
1
tb  t a

tb
ta
f e2 (t ).dt
 eab
O mínimo dessa função será encontrado impondo:  c  0
12
Por essa técnica chega-se à relação seguinte (ver demonstração): 1
C12 

b
a
f1 (t ). f 2 (t ) dt

b
a
f 22 (t ).dt
Se f1 e f2 forem ortogonais, então C12 é nulo no intervalo dado. No caso da série de Fourier
1
Demonstração:
eab 
1
tb  t a
  f (t )  C
tb
ta
1
eab
  1


C12
C12  tb  ta

tb
ta
 f 2 (t ) .dt
2
12
f
2
1


(t )  2C12 f1 (t ) f 2 (t )  C 212 . f 22 (t ) .dt   0

 2C12  f 22 (t ).dt  2  f1 (t ). f 2 (t ).dt  0
 C12


b
a
f1 (t ). f 2 (t )dt

b
a
f 22 (t ).dt
DSE – FEEC - UNICAMP
4
Avaliação da Qualidade da Energia Elétrica
S.M.Deckmann e J.A.Pomilio
obtém-se, por analogia, que:
Seja f2(t)=1,

A0 
  f ( t ).1. d t  1  f ( t ) . dt  valor médio no período

2  
1
.
d

t




Seja f2(t)=cos(h1t),

Ah
 f ( t ) .cos( h t ).dt  1  f ( t ). cos( h t ).dt
  
 
  cos ( h t ).dt
1

1

2
1

Seja f2(t)=sen(h1t),

Bh
 f (  t ).sen( h t ).d t  1  f ( t ) .sen( h t ).dt
  
 
  sen ( h t ) .dt
1

1

2
1

Cada coeficiente pode ser interpretado como sendo o dobro do valor médio da função,
ponderado pela respectiva base harmônica. Notar que os coeficientes (das funções seno ou cosseno)
serão números reais, podendo ser positivos ou negativos. Uma vez obtidos os coeficientes, pode-se
dispor o espectro na forma seguinte:
A
1
1/3
1/5
2f1
f1
4f1
5f1
3f1
f
-1/4
-1/2
Figura 3.7 Espectro de amplitude da onda dente de serra.
Como se pode notar, coeficientes negativos correspondem à fase de 180.
3.5 Representação da Série de Fourier na Forma Exponencial
Existem vantagens para a manipulação algébrica em usar a representação da série de Fourier
pela correspondente série exponencial complexa, ao invés de usar funções seno e cosseno:
f (t ) 

 a .e
h  
onde:
jh1t
h
h  0,  1,  2,...
ah = coeficiente complexo
DSE – FEEC - UNICAMP
5
Avaliação da Qualidade da Energia Elétrica
S.M.Deckmann e J.A.Pomilio
Notar que para h = 0 resulta o termo médio (CC) e para h = 1 resulta a onda fundamental.
Isso pode ser verificado impondo-se as condições de simetria par e ímpar:
se a h = a -h resulta termo cosseno
se a.h = -a -h resulta termo seno
Para verificar, basta considerar que:
e jt  e  jt
 sen t
2j
e jt  e  jt
 cos t
2
 e jt  e  jt  2 j sen t
resultando a forma de Euler: e j..t = cos t + j.sent
Uma vez que h pode assumir valores positivos e negativos, diz-se que essa série é bilateral.
3.5.1 Série Exponencial Complexa Unilateral
Pode-se rearranjar a soma bilateral na forma de série exponencial unilateral:


f (t )  a 0   a h e
h 1
j h 1 t
 a h e
 j h 1 t

h=1, 2, 3...
Para sinais reais, a condição de simetria complexa tem que ser satisfeita, ou seja, a  h  a h 2,
devido ao teorema de Parseval (a energia deve se manter tanto no domínio do tempo como no da
frequência). Portanto:


f (t )  a0   ah .e jh1t  ah .e  jh1t
h 1

(I)
Assumindo ainda que cada coeficiente complexo é formado pelas partes real e imaginária na forma:
1
h > 0,
ah   Ah  j Bh 
2
1
 Ah  jBh 
2
resulta que a equação (I) pode ser escrita como:
de modo que:
a h  ah 

f (t )  a0    Ah cos(h1t )  Bh sen(h1t )
h 1
que é a própria série de Fourier de cossenos e senos formulada inicialmente.
Portanto, as três formas de representação da série de Fourier:
série de senos e cossenos;
série exponencial complexa bilateral;
série exponencial complexa unilateral,
são equivalentes e intercambiáveis.
Com os coeficientes de uma série pode-se determinar os coeficientes da outra.
2
O símbolo * indica o valor complexo conjugado (possui a mesma parte real e a parte imaginária tem o sinal trocado).
DSE – FEEC - UNICAMP
6
Avaliação da Qualidade da Energia Elétrica
S.M.Deckmann e J.A.Pomilio
3.6. Da Série de Fourier à Transformada de Fourier
Existe uma relação direta entre a forma exponencial complexa e a forma em termos de senos e
cossenos da série de Fourier. Devido à relação entre os coeficientes das duas formas, para h > 0:
1
1
ah   Ah  jBh 
a h   Ah  jBh 
2
2
pode-se obter os coeficientes complexos ah a partir dos coeficientes reais Ah e Bh:
Ah 
1 
f (t ) cos(h1t ). dt
 
Bh 
1 
f (t ).sen(h1t ).dt
 
resultando:
ah 
1 
f (t )cos(h1t )  j.sen(h1t ). dt
2 
ah 
1 
f (t ) . e  j h 1 t . dt
2 
h = 0, 1, 2....
 jh t
1
Notar que e
é um operador de rotação cuja amplitude é 1. Portanto, cada coeficiente ah
corresponde ao valor médio da função f(t), ponderada pelo operador que gira com velocidade h1, a
qual define a periodicidade harmônica.
3.6.1 Análise de um Sinal com Especial Interesse: O Trem de Pulsos
f(x)
2/k
1
-
x=0

2
x=1t
T1
Figura 3.8 Trem de pulsos unitários.
Esse sinal é importante para se chegar à Transformada de Fourier. Por conveniência, tome-se
2
2
o sinal com período T1 
, o pulso com amplitude 1 e duração t=
. Notar que k inteiro pode
k
1
ser interpretado como uma frequência múltipla de 1, uma vez que t é uma fração de T1.
Sabe-se que os coeficientes da série complexa de Fourier são dados por:

1
ah 
2
k
 e

 jhx
. dx
para
h=0, 1, 2...
k
resultando para:
e para
x = 1t
1
2
   1
 k  k   k
h=0
a0 
h0
1
ah 
e  jhx
 jh2
DSE – FEEC - UNICAMP



k


j mh 
1   jh k
1
 
e k  
sen h 
e
 =

 jh2 
 k
k
 h
7
Avaliação da Qualidade da Energia Elétrica
S.M.Deckmann e J.A.Pomilio
Logo, o trem de pulsos pode ser escrito como sendo a série:

sen(h )

1
k .e j m x 
f ( x)   .
ah . e j h x


h   k
h 
h
k

h=0, 1, 2....

sen(h )
1
k
onde os coeficientes valem: ah  .

k
h
k

sen(h )
k é chamada função sinc(.) e, para argumento contínuo, apresenta a
A função

h
k
seguinte forma:
Figura 3.9 Função sinc(.).
Essa função define a envoltória para os valores dos coeficientes ah do trem de pulsos. No
caso do trem de pulsos, verifica-se que os coeficientes são definidos para as abcissas da função sinc
apenas para valores específicos ou discretos, dados por:
h
 2 3
 0, ,
,
,.... pois h=0, 1, 2, 3....
k
k
k
k
Pode-se visualizar o que ocorre com os coeficientes ah se os representarmos para dois casos,
por exemplo, k=3 e k=5:
Figura 3.10 Coeficientes ah do trem de pulsos para k=3.
DSE – FEEC - UNICAMP
8
Avaliação da Qualidade da Energia Elétrica
S.M.Deckmann e J.A.Pomilio
Figura 3.11 Coeficientes am do trem de pulsos para k=5.
Quanto menor a duração do pulso (maior k), mais os coeficientes se aproximam e diminuem
de amplitude. Se, ao invés de reduzir a duração, aumentar o período entre pulsos (T1 ), tem-se, no
limite, um trem de pulsos com período infinito, ou seja, apenas um pulso na origem. Com isso, a
frequência fundamental (  1  2 ) tende a zero, e os componentes se aproximam tanto que formam
T1
um espectro contínuo com amplitudes infinitesimais:
ah 
1
2


T /2
f ( x).e  jhx .dx 

1 1
f (t ).e  jh1t .dt

T1 T1 / 2
Como ah tende a zero, enquanto T1 tende a infinito, o produto ah.T1 tende a uma constante:

ahT1   f (t ).e  j  t . dt  ( )
(T  )
1

A função contínua () é chamada transformada ou integral de Fourier.
A função inversa é obtida da série:
f (t ) 
( ) j h1 t 

1
.e
  ( ) 1 . e j mh1 t 
2
2
h   T1
h  




a
h
T
1



( ).e j h t . d

1
notar os limites usados para essas associações de operações contínuas e discretas:
T1  
1  d
h.1  



Resumindo: A Transformada de Fourier (TF) mapeia sinais aperiódicos para o domínio da
frequência, resultando um espectro contínuo através da Integral de Fourier:


1
(  )   f ( t ). e  j  t . dt
f (t ) 
().e j t . d

2  

DSE – FEEC - UNICAMP
9
Avaliação da Qualidade da Energia Elétrica
S.M.Deckmann e J.A.Pomilio
3.6.2 Exemplos de aplicação:
a) Obter a TF da seguinte onda retangular com período T1 
2
1
:
A
-

t
T1
Figura 3.12 Trem de pulsos
Os coeficientes da TF são:

1
2
a0 
A . dt 
A

T1 
T1
(média do período)
e o termo genérico, de ordem h, vale:

1
A
A.2
 jh  t
ah   A . e 1 . dt 
. e  j h1  e j h1 
. sen(h1 ) (h  0)
T1 
 jh1T1
h1T1


portanto, multiplicando numerador e denominador por :
 2 
sen h  
2A sen(h1 ) 2A
 T1 
ah 
.

.
2
T1
h1
T1
h 
T1
Esse coeficiente se anula cada vez que o argumento se torna múltiplo de , ou seja, quando
2
(inteiro).
h.
T1
n
Para n=1 temos h  T1 representa o inverso do ciclo de trabalho.
2
Figura 3.13 Coeficientes da Transformada de Fourier da onda retangular.
Portanto, para a onda periódica resulta um espectro discreto, cuja resolução é dada por
2
   1 
.
T1
Notar que a duração do pulso (2) define a largura da faixa de frequências (primeiro
cruzamento da função sinc por zero).
DSE – FEEC - UNICAMP
10
Avaliação da Qualidade da Energia Elétrica
S.M.Deckmann e J.A.Pomilio
b) Transformada de Fourier do pulso isolado:
A
A

-
t
Figura 3.14
Pulso isolado e respectivo espectro contínuo.
Neste caso, como T1   , o pulso é expresso por:
f (t ) 

 a T .e
h
jh1t
h 1
 T1 / 2

    f (t ).e  jh1t .dt .e jh1t
h

T1 / 2

(  )  ahT1 
portanto a TF é dada por:
T1 / 2
 f (t ).e
 jh1t
.dt
T1 / 2
a0T1 
e
T1 / 2

T1 / 2

 f (t ).dt   f (t ).dt  2 . A
Notar que para o pulso isolado o espectro é uma função contínua de .
A duração do pulso (2) continua definindo a largura da faixa de frequência do lóbulo
principal.
No caso do pulso ser estreito, o espectro se alarga na proporção inversa da duração do pulso
(2), enquanto que a amplitude diminui.
A
- 
t
Figura 3.15
Pulso isolado estreito e seu espectro contínuo.
No caso de pulso largo, acontece o oposto, o espectro se estreita e aumenta amplitude em
torno da origem:
DSE – FEEC - UNICAMP
11
Avaliação da Qualidade da Energia Elétrica
S.M.Deckmann e J.A.Pomilio
A

-
Figura 3.16
t
Pulso isolado largo e seu espectro contínuo.
Continuando essa expansão da duração do pulso, pode-se, no limite, considerar o degrau
como um pulso de duração infinita, daí o seu espectro de concentrar em um impulso na origem.
0
Figura 3.17

Espectro do degrau.
A questão pendente, que será respondida na sequência é: quanto vale a amplitude da “vareta”
do espectro do degrau?
3.7 Da Transformada de Fourier à Transformada de Laplace
Para existir a TF é preciso que no intervalo -  t   a integral seja finita, ou seja:



f ( t ). e  j t dt  

Como e-j..t tem magnitude 1, uma condição suficiente é que:


f ( t ) . dt  
Porém, essa condição não é satisfeita por várias funções de interesse prático, como as funções
seno, cosseno, degrau, as quais, portanto, não possuem Transformada de Fourier. No entanto,
limitando as funções periódicas entre -T e +T e depois fazendo T  pode-se obter a transformada.
Para o degrau u(t), pode-se utilizar outro processo, que é supor decaimento exponencial (e-.t ) do
degrau, e fazer o valor da atenuação tender a zero ( 0) após calcular a transformada.
1
e-t
t
0
Figura 3.18 Função atenuação do degrau.
A Transformada de Fourier G() da função atenuação do degrau é:

G(  )   e  t . e  j t . dt 
0

1
e  t .e  j t
 (   j )


0

1
  j
( >0)
Para obter o espectro do degrau não basta zerar , pois em =0 ocorre uma singularidade.
DSE – FEEC - UNICAMP
12
Avaliação da Qualidade da Energia Elétrica
S.M.Deckmann e J.A.Pomilio
Levantando a singularidade, vê-se que para =0, resulta: G( 0 ) 
G(  ) 
1

; e, para >>0, resulta:
1
. Ou seja, o espectro é contínuo e decrescente. A fase inicial é zero e atrasa até -90.
j
G(  )
1/
Degrau unitário

1
G(  )
0

t
-90
Figura 3.19 Transformada de Fourier do degrau unitário.
3.7.1 A Transformada de Laplace
Incorporando-se a técnica de atenuação à Transformada de Fourier, resulta a Transformada
de Laplace.


0
0
G a (  )   f ( t ). e  t .e  j  t . dt   f ( t ).e (   j  ).t . dt
Designando s    j resulta:

L( s )   f ( t ). e  s t . dt
0
A integral agora tem que começar em t=0 uma vez que para t<0 a atenuação vira ampliação, e
portanto a integral se torna divergente.
3.7.2 Comparação da Transformada de Laplace e de Fourier
Uma vez que:
(  )  


 j t
f ( t ). e
. dt

L( s )   f ( t ). e  s t . dt
0
percebe-se que, enquanto Fourier expande f(t) em um conjunto infinito de exponenciais tipo ej..t, que
dão origem a senos e cossenos sobre todo o intervalo - < t < , Laplace expande f(t) em um
conjunto infinito de exponenciais complexas tipo es.t, que dão origem não apenas a senos e cossenos,
como também a exponenciais crescentes e decrescentes, e combinações deles, resultando modos
oscilatórios decrescentes (amortecidos) e crescentes (instáveis).
Essa é uma importante generalização, mas que só se aplica para t  0. Essa transformação
atende a grande parte dos sinais físicos e por isso encontrou grande aplicação na área de controle
DSE – FEEC - UNICAMP
13
Avaliação da Qualidade da Energia Elétrica
S.M.Deckmann e J.A.Pomilio
moderno. Neste caso, convertendo cada sinal para o domínio da frequência pela transformada de
Laplace, descobre-se que a função de transferência descreve a relação entrada-saída dos dispositivos
que intervêm no processo.
Sistemas complicados podem ser analisados através das relações matemáticas no domínio da
frequência, gerando funções complexas H(s) que podem ser decompostas em pólos e zeros que são as
raízes dos polinômios do denominador e numerador de H(s). Os pólos e zeros podem ser usados para
caracterizar o comportamento dinâmico do sistema sob diferentes condições de excitação e controle.
Porém esse é assunto para outro curso.
DSE – FEEC - UNICAMP
14
Avaliação da Qualidade da Energia Elétrica
S.M.Deckmann e J.A.Pomilio
Apêndice: Exemplos de uso do MathCad para análise de Fourier
Ondas periódicas e aperiódicas
t  0  .001  3
s1( t)  2 cos( 15 t)  5 sin ( 20 t)
10
5
s1( t)
0
5
10
0
0.5
1
1.5
2
2.5
3
t
O máximo divisor comum entre as frequências de cada onda períodica é 5, logo o período é:
 5   1
To  
 
2



 
s1( 0)  2
s1( To )  2
To  1.257
Seja outra forma de onda:
s2( t)  2 cos( 15 t)  1 cos 10  t
4
2
s2( t)
0
2
4
0
0.5
1
1.5
t
2
2.5
3
Embora cada sinal, individualmente, seja periódico, como as frequencia não estão em uma
relação RACIONAL, ou seja, NÃO SÃO MÚLTIPLAS inteiras de um fator comum, a onda
resultante não é periódica
DSE – FEEC - UNICAMP
15
Avaliação da Qualidade da Energia Elétrica
S.M.Deckmann e J.A.Pomilio
Coeficientes da série de Fourier para a onda s1(t)
w1  2 

To
To
2
1 
Ao 

s1( t) d t
To  To

2
Ao  0
n  1  10
To
2
2 
An 

s1( t) cos[ n ( w1 ) t] d t
To  To

2
To
2
2 
Bn 

s1( t) sin ( n w1 t) d t
To  To

2
An 
0
Bn 
0
0
-1.502·10 -15
2
0
0
0
5
-1.034·10
0
0
0
0
-15
0
-1.612·10
-15
0
4.736·10 -15
0
0
DSE – FEEC - UNICAMP
16
Avaliação da Qualidade da Energia Elétrica
Outra forma de onda
S.M.Deckmann e J.A.Pomilio
s1( t)  sign( cos( 15 t) ) 
1
2
2
s1( t)
0
0
0.5
1
1.5
2
2.5
3
t
w1  15
To  2 

w1
To  0.419
To
2
1 
Ao 

s1( t) d t
To  To

Ao  0.5
2
n  1  10
To
2
2 
An 

s1( t) cos[ n ( w1 ) t] d t
To  To

2
An 
1.273
Bn 
0
0
-0.424
0
0
0
0.255
0
0
0
-0.182
0
0
0
0.141
0
0
0
DSE – FEEC - UNICAMP
To
2
2 
Bn 

s1( t) sin ( n w1 t) d t
To  To

2
17
Avaliação da Qualidade da Energia Elétrica
S.M.Deckmann e J.A.Pomilio
Reconstrução do sinal:
x( t)  Ao  A1 cos( w1 t)
2
x( t)
0
2
0
0.5
1
1.5
2
2.5
3
t
x( t)  Ao  A1 cos( w1 t)  A3 cos( 3 w1 t)
2
x( t)
0
2
0
0.5
1
1.5
2
2.5
3
t
x( t)  Ao  A1 cos( w1 t)  A3 cos( 3 w1 t)  A5 cos( 5 w1 t)
2
x( t)
0
2
0
0.5
1
1.5
2
2.5
3
t
x( t)  Ao  A1 cos( w1 t)  A3 cos( 3 w1 t)  A5 cos( 5 w1 t)  A7 cos( 7 w1 t)
2
1
x( t)
0
1
0
0.5
1
1.5
t
DSE – FEEC - UNICAMP
18
2
2.5
3
Avaliação da Qualidade da Energia Elétrica
S.M.Deckmann e J.A.Pomilio
E  2
Outra forma de onda
s1( t)  E  cos( w1 t)

2
s1( t)
1
0
0
0.5
1
1.5
2
2.5
3
t
To 
 2
w1
To  0.419
To
2
1 
Ao 

s1( t) d t
To  To

2
Termo geral, para n par:
n
Ao  1.273
An 
n  1  10
4  (  1)
2
1  n2 
To
2
2 
An 

s1( t)  cos[ n ( w1 ) t] d t
To  To

2
To
2
2 
Bn 

s1( t)  sin ( n w1 t) d t
To  To

2
DSE – FEEC - UNICAMP
An 
Bn 
0
0
0.849
0
0
0
-0.17
0
0
0
0.073
0
0
0
-0.04
0
0
0
0.026
0
19
E
Avaliação da Qualidade da Energia Elétrica
S.M.Deckmann e J.A.Pomilio
Reconstrução do sinal
x( t)  Ao  A1 cos( w1 t)
1.276
1.274
x( t)
1.272
1.27
0
0.5
1
1.5
2
2.5
3
t
x( t)  Ao  A1 cos( w1 t)  A2 cos( 2 w1 t)
3
2
x( t)
1
0
0
0.5
1
1.5
2
2.5
3
t
x( t)  Ao  A1 cos( w1 t)  A2 cos( 2 w1 t)  A4 cos( 4 w1 t)
2
x( t)
1
0
0
0.5
1
1.5
2
2.5
3
t
x( t)  Ao  A1 cos( w1 t)  A2 cos( 2 w1 t)  A4 cos( 4 w1 t)  A6 cos( 6 w1 t)
3
2
x( t)
1
0
0
0.5
1
1.5
t
DSE – FEEC - UNICAMP
20
2
2.5
3
Avaliação da Qualidade da Energia Elétrica
S.M.Deckmann e J.A.Pomilio
Análise de Trem de Pulsos
Pulso de largura variável
t  0  0.0001  1
w1  2  5
s1( t) 
sign cos 2  5 t  0.9   1
2
To  2 

w1
1
s1( t) 0.5
0
0
0.2
0.4
0.6
0.8
1
t
To  0.2
n  1  30
To
2
1 
Ao 

s1( t) d t
To  To

Ao  0.144
2
An 
0.277
0.251
0.209
0.156
0.099
0.045
-1.419·10 -3
To
2
2 
An 

s1( t) cos[ n ( w1 ) t] d t
To  To

2
To
2
2 
Bn 

s1( t) sin ( n w1 t) d t
To  To

2
Bn 
0
0
-0.036
0
-0.056
0
-0.063
0
-0.057
0
-0.04
0
-0.02
0
1.419·10 -3
0
0.02
0.032
DSE – FEEC - UNICAMP
21
Avaliação da Qualidade da Energia Elétrica
S.M.Deckmann e J.A.Pomilio
Reconstrução do sinal
x( t)  Ao  A1 cos( w1 t)
0.5
x( t)
0
0.5
0
5
x( t)  Ao 

0.2
0.4
0.6
0.8
1
t
 Ancos( n w1 t)  Bnsin ( n w1 t) 
n1
2
1
x( t)
0
1
0
0.2
0.4
0.6
0.8
1
0.8
1
t
30
x( t)  Ao 

 Ancos( n w1 t)  Bnsin ( n w1 t) 
n1
1.5
1
x( t)
0.5
0
0.5
0
0.2
0.4
0.6
t
DSE – FEEC - UNICAMP
22
Avaliação da Qualidade da Energia Elétrica
S.M.Deckmann e J.A.Pomilio
Análise dos coeficientes
n  0  40
To
2
1 
 inw1 t
an 

s1( t) e
dt

To  To

an 
0.144
2
0.139
0.125
0.104
0.077
0.049
0.15
0.022
-7.097·10 -4
-0.018
-0.028
0.1
-0.032
an
-0.028
-0.02
-9.981·10 -3
0.05
7.097·10 -4
9.842·10 -3
0
0.016
0.019
0.05
0.017
0
4
8 12 16 20 24 28 32 36 40
0.013
6.26·10 -3
n
-7.096·10 -4
-6.91·10 -3
-0.011
-0.013
-0.012
-9.115·10 -3
-4.468·10 -3
7.095·10 -4
5.393·10 -3
8.722·10 -3
DSE – FEEC - UNICAMP
23
Avaliação da Qualidade da Energia Elétrica
S.M.Deckmann e J.A.Pomilio
Em direção ao impulso isolado e seu espectro contínuo e constante:
t  0  0.0001  0.2
w1  2  5
s1( t) 
sign cos 2  5 t  0.995   1
2
To  2 

w1
1
s1( t) 0.5
0
0
0.05
0.1
0.15
0.2
t
To
2
1 
 inw1 t
an 

s1( t) e
dt
To  To

To  0.2
2
an 
0.032
0.032
0.032
0.031
0.031
0.031
0.05
0.03
0.029
0.029
an
0
0.028
0.027
0.026
0.05
0.025
0.024
0.022
0
4
8
12 16 20 24 28 32 36 40
n
DSE – FEEC - UNICAMP
24
0.021
Avaliação da Qualidade da Energia Elétrica
DSE – FEEC - UNICAMP
S.M.Deckmann e J.A.Pomilio
25