Poliedro

Poliedro
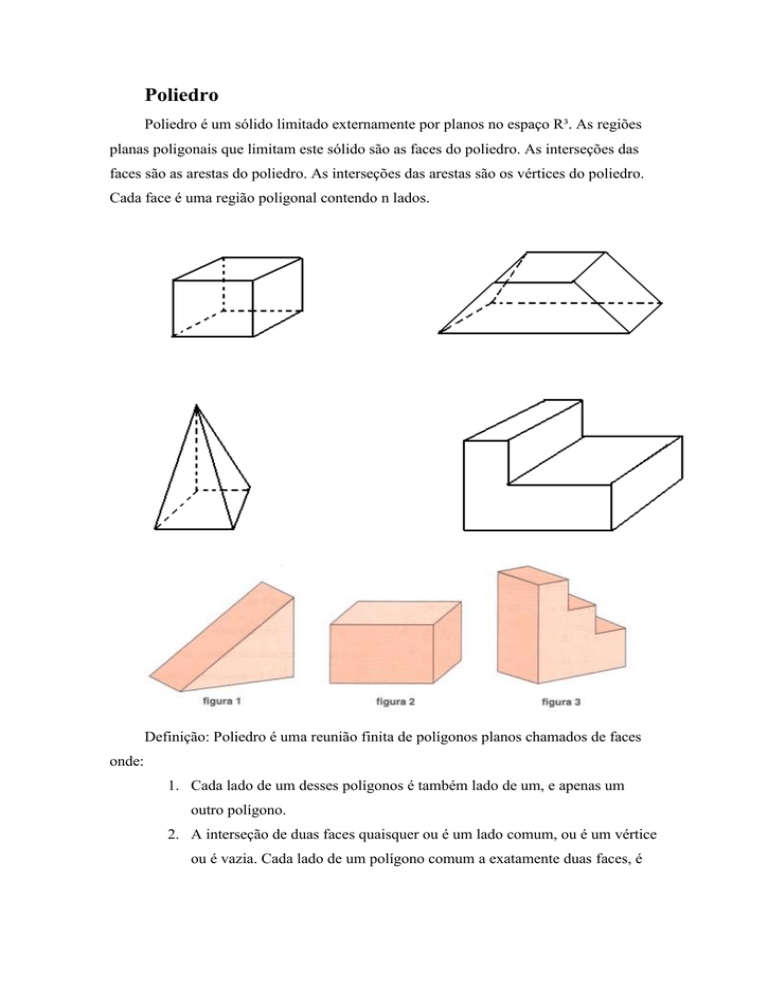
Poliedro é um sólido limitado externamente por planos no espaço R³. As regiões
planas poligonais que limitam este sólido são as faces do poliedro. As interseções das
faces são as arestas do poliedro. As interseções das arestas são os vértices do poliedro.
Cada face é uma região poligonal contendo n lados.
Definição: Poliedro é uma reunião finita de polígonos planos chamados de faces
onde:
1. Cada lado de um desses polígonos é também lado de um, e apenas um
outro polígono.
2. A interseção de duas faces quaisquer ou é um lado comum, ou é um vértice
ou é vazia. Cada lado de um polígono comum a exatamente duas faces, é
chamado uma aresta do poliedro e cada vértice de uma face é um vértice
do poliedro.
Exemplo de não poliedro.
Poliedros convexos:
Todo poliedro limita uma região do espaço chamada de interior desse poliedro.
Dizemos que um poliedro é convexo se o seu interior é convexo.
Definição de convexo: “um conjunto C, do plano ou do espaço, diz-se convexo,
quando qualquer segmento de reta que liga dois pontos de C esta inteiramente contido
em C”
Definição: Um poliedro é convexo se qualquer reta o corta em no Maximo, dois
pontos.
Observação: A reunião das faces de um poliedro convexo é denominada
superfície poliédrica fechada
Poliedros convexos são aqueles cujos ângulos formados por planos adjacentes têm
medidas menores do que 180 graus.
Abaixo, veja mais exemplos de poliedros convexos e suas planificações:
Abaixo, veja mais exemplos de poliedros não convexos.
Duas Desigualdades Importantes (para poliedros convexos);
V(numero de vértices)
F(faces)
A(arestas)
1. 2A  3F
2. 2A  3V
Relação de Euler
Para todos poliedros convexos vale a seguinte relação;
V(numero de vértices)
V+F=A+2
F(faces)
ou
A(arestas)
V-A+F=2
Essa relação foi descoberta e demonstrada pelo matemático suíço Leonhard
Euler (1707-1708).
Observação: Todo poliedro convexo é euleriano, mas nem todo poliedro
euleriano é convexo.
Poliedro A
Poliedro D
V
A
F
Poliedro E
VA+F
V
A
F
6
9
VA+F
tetraedro
4
6
4
2
prisma de base triangular
5
2
cubo
8
12
6
2
prisma de base pentagonal 10 15 12
2
octaedro
6
12
8
2
prisma de base n-gonal
2n 3n n+2
2
dodecaedro
20 30
12
2
pirâmide de base quadrada
5
8
5
2
icosaedro
12 30
20
2
pirâmide de base
12
7
2
12 18
8
2
hexagonal
7
poliedro A
poliedro D
16 32
16
0
pirâmide de base n-gonal
n+1 2n n+1
2
poliedro E
28 60 30
-2
Exemplos.
A bola de futebol que apareceu pela primeira vez na copa de 70 foi inspirada em um
conhecido poliedro convexo formado por 12 faces pentagonais e 20 faces hexagonais, todas
regulares. Pergunta-se quantos vértices possui tal poliedro.
Temos 12 faces pentagonais e 20 faces hexagonais no total de 32 faces F=32.
Encontrar o numero de arestas do poliedro A (arestas):
2A=5F 5 +6F 6 =5*12+6*20=180
A=90
Como o poliedro e convexo vale a relação de Euler V-A+F=2, de onde concluímos que
V=60.
Poliedros de Platão
Um poliedro é chamado poliedro de Platão quando satisfaz três condições:
1. Condição: Todas as faces têm o mesmo número (n) de arestas. n.F=2A
2. Condição: Todos os vértices são pontos em que concorre o mesmo número (m) de
arestas. m.V=2A
3. Condição: O poliedro é euleriano, isto é, V - A + F = 2.
Observação: Existem cinco, e somente cinco, tipos de poliedros de Platão.
m
n
A
V
F
Nome
3
3
6
4
4
tetraedro
3
4
12
8
6
hexaedro
4
3
12
6
8
octaedro
3
5
30
20
12
dodecaedro
5
3
30
12
20
icosaedro
Poliedros regulares
Um poliedro convexo é regular quando:

Suas faces são polígonos regulares e congruentes.

Em todos os seus vértices concorre o mesmo número de arestas.
Num poliedro regular, percebe-se imediatamente que:

Todas as faces têm o mesmo número de arestas (pois as faces são congruentes);

Todos os vértices são pontos em que concorre o mesmo número de arestas;

O poliedro é euleriano (pois é convexo).
Assim, todo poliedro regular é poliedro de Platão. Por isso, existem cinco tipos de
poliedros regulares:
Tetraedro
hexaedro
octaedro
dodecaedro
icosaedro
Teorema. Existem apenas cinco poliedros regulares convexos.
Para demonstrar, seja n o numero de lados de cada face e seja p o numero de arestas que
concorrem em cada vértice. Temos 2A=nF=pV ou A=
nF
nF
e V=
.
2
p
Substituindo na relação de Euler obtemos
F=
4p
.
2 p  2n  pn
nF nF
+F=2
2
p
2p+2n-np<0
Como p  3, chegamos a n < 6. As possibilidades são então as seguintes:
. n = 3  F=
n = 4  F=
4p
6 p
n = 5  F=
4p
10  3 p
2p
4 p
Prismas
Definição e Elementos
Prisma é um poliedro convexo tal que duas faces são polígonos congruentes situados
em planos paralelos e as demais faces são paralelogramos.
Nomenclatura e Classificação
Os prismas recebem nomes de acordo com os polígonos das bases.
Assim:
• um prisma é triangular quando suas bases são triângulos;
• um prisma é quadrangular quando suas bases são quadriláteros;
• um prisma é pentagonal quando suas bases são pentagonais;
• um prisma é hexagonal quando suas bases são hexagonais.
...
Quando as arestas laterais de um prisma forem perpendiculares aos planos das bases, o
prisma é chamado de reto; caso contrário, de oblíquo.
.
Exemplos
Cubo
Definição e Elementos
Cubo é um prisma em que todas as faces são quadradas. O cubo é um prisma
quadrangular regular cuja altura é igual à medida da aresta da base.
O cubo da figura tem arestas de medida l, então,
• as diagonais de suas faces medem l
, pois são diagonais de quadrados de lados
com medidas iguais a l.
• as diagonais do cubo medem l
, pois:
Assim:
Paralelepípedos
Definição
Chamamos de paralelepípedo o prisma cujas bases são paralelogramos; dessa
forma, todas as faces de um paralelepípedo são paralelogramos.
Exemplos
Paralelepípedo Reto Retângulo
Diagonais de um
paralelepípedo retângulo
No paralelepípedo da figura com dimensões a, b e c, sejam d1 e d, as diagonais da
face ABCD e do paralelepípedo, respectivamente.
No triângulo ABC, temos:
AC2 = AB2 + BC2
ou então,
No triângulo ACG, temos:
AG2 = AC2 + CG2
ou então,
Como
, temos:
d2 = a2 + c2 + b2 ou
Exercícios resolvidos:
(VUNESP – 07) Calcular o volume de um paralelepípedo retângulo, sabendo
que suas dimensões são proporcionais a 9, 12 e 20, e que a diagonal mede 100 m.
Resolução
d2 = a2 + b2 + c2
1002 = (20k)2 + (12k)2 + (9k)2
1002 = 625k2
Assim, 25k = 100
k=4
Então, a = 20 · 4 = 80 m
b = 12 · 4 = 48 m
c = 9 · 4 = 36 m
V = a · b · c = 80 · 48 · 36
(Fuvest-SP) Dois blocos de alumínio, em forma de cubo, com arestas medindo
10 cm e 6 cm, são levados juntos à fusão e em seguida o alumínio líquido é
moldado como um paralelepípedo reto de arestas 8 cm, 8 cm e x cm. O valor de
x é:
a) 16 m
d) 19 m
b) 17 m
e) 20 m
c) 18 m
Resposta: D
Pelo enunciado, o volume do paralelepípedo é igual à soma dos volumes dos
cubos.
Assim,
8 · 8 · x = 63 + 103
64 x = 216 + 1 000
64 x = 1 216
x = 19
(Mackenzie-SP) Um prisma regular triangular tem todas as arestas
congruentes e 48 m2 de área lateral. Seu volume vale
a) 16 m3
d)
b) 32 m3
e)
c) 64 m3
Resolução
(Mackenzie-SP 2000) Se a soma dos ângulos internos de todas as faces de um
prisma é 6 480°, então o número de lados da base do prisma é
a) 8
d) 12
b) 9
e) 15
c) 10
Resolução
Sendo n o número de lados da base do prisma, então este possui n faces laterais
quadrangulares e duas faces que são polígonos de n lados. Portanto, a soma dos
ângulos internos de todas as sua faces é
n · 360° + 2 · (n – 2) · 180°
Conseqüentemente,
n · 360° + 2 · (n – 2) · 180° = 6 480°
Resposta: C
O conceito de pirâmide
n = 10
Pirâmides
Consideremos um polígono contido em um plano (por exemplo, o plano
horizontal) e um ponto V localizado fora desse plano. Uma Pirâmide é a reunião de
todos os segmentos que têm uma extremidade em V e a outra num ponto qualquer do
polígono. O ponto V recebe o nome de vértice da pirâmide.
Exemplo: As pirâmides do Egito, eram utilizadas para sepultar faraós, bem como
as pirâmides no México e nos Andes, que serviam a finalidades de adoração aos seus
deuses. As formas piramidais eram usadas por tribos indígenas e mais recentemente por
escoteiros para construir barracas.
Elementos de uma pirâmide
Em uma pirâmide, podemos identificar vários elementos:
Base: A base da pirâmide é a região plana poligonal sobre a qual se apoia a
pirâmide.
Vértice o vértice da pirâmide: é o ponto isolado P mais distante da base da
pirâmide.
Eixo: Quando a base possui um ponto central, isto é, quando a região poligonal é
simétrica ou regular, o eixo da pirâmide é a reta que passa pelo vértice e pelo centro da
base.
Altura: Distância do vértice da pirâmide ao plano da base.
Faces laterais: São regiões planas triangulares que passam pelo vértice da pirâmide
e por dois vértices consecutivos da base.
Arestas Laterais: São segmentos que têm um extremo no vértice da pirâmide e
outro extremo num vértice do polígono situado no plano da base.
Apótema: É a altura de cada face lateral.
Superfície Lateral: É a superfície poliédrica formada por todas as faces laterais.
Aresta da base: É qualquer um dos lados do polígono da base.
Classificação das pirâmides pelo número de lados da base
triangular
quadrangular
base:triângulo
base:quadrado
Pirâmide Regular reta
pentagonal
base:pentágon
o
hexagonal
base:hexágono
Pirâmide regular reta é aquela que tem uma base poligonal regular e a projeção
ortogonal do vértice V sobre o plano da base coincide com o centro da base.
R raio do circulo circunscrito
r
raio do círculo inscrito
l
aresta da base
a
p
h
a
l
apótema de uma face lateral
altura da pirâmide
aresta lateral
As faces laterais são triângulos isósceles congruentes
Às vezes podemos construir fórmulas para obter as áreas das superfícies que
envolvem um determinado sólido. Tal processo é conhecido como a planificação desse
sólido. Isto pode ser realizado se tomarmos o sólido de forma que a sua superfície
externa seja feita de papelão ou algum outro material.
No caso da pirâmide, a idéia é tomar uma tesoura e cortar (o papelão d)a pirâmide
exatamente sobre as arestas, depois reunimos as regiões obtidas num plano que pode ser
o plano de uma mesa.
As regiões planas obtidas são congruentes às faces laterais e também à base da
pirâmide.
Analise do livro
O livro e muito bom por sinal apresenta muitas ilustrações exemplos e exercícios
trazendo sempre exemplos para explicar e tentar ajudar o aluno no decorrer do conteúdo.
Porem o livro começa tacando os poliedros e exemplos do mesmo mais não define
nada formalmente deixando o conteúdo em aberto assim também acontece com conexos
e relação de Euler. O livro também não trás os sólidos de Platão entrando direto nos
poliedros regulares não mostrando ao aluno que existem os sólidos de Platão e todos
são poliedros regulares.
Em pirâmide e prismas o livro também não define e nem constrói a relações
corretamente deixando sempre o conteúdo em aberto mas tenta por exemplos defini
pirâmides e prismas sem nem uma construção ou definição apropriada para a serie.
Em poliedros o livro comete alguns erros de não trazer as notações antes de
utilizaras podendo deixar o aluno confuso ou sem saber que A,F,V são as arestas faces e
vértices do poliedro.
No geral o livro e muito bom trazendo muitos exemplos exercícios e planificações
do conteúdo a bordado e apropriado como material de auxilio pedagógico.