alguns exercícios resolvidos

FÍSICA – Trabalho & Energia – 2º EM
Avaliação Mensal
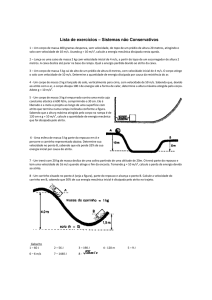
1. O gráfico velocidade contra tempo, mostrado adiante, representa o movimento
retilíneo de um carro de massa m = 600kg numa estrada molhada. No instante t = 6s
o motorista vê um engarrafamento à sua frente e pisa no freio. O carro, então, com
as rodas travadas, desliza na pista até parar completamente. Despreze a resistência
do ar.
a) Qual é o coeficiente de atrito entre os pneus do carro e a pista?
b) Qual o trabalho, em módulo, realizado pela força de atrito entre os instantes t = 6s
e t = 8s?
Resolução:
Dados:
m = 600 kg;
g = 10 m/s² (adotado como valor padrão);
valores obtidos do gráfico;
Item (a)
As únicas forças que agem sobre o veículo no instante da frenagem são peso, reação normal e
atrito.
Supondo a superfície horizontal, podemos dizer então que a força de atrito é a única força na direção
do deslocamento. Dessa forma podemos afirmar que:
FR = m·a
Mas como
FR = -FAT
e
-Fat = µ·FN
Temos
-FAT = m·a
µ·FN = -m·a
µ·( m·g) = -m·a
µ = -a / g
Do gráfico podemos calcular a aceleração:
a = (0 – 10) / (8 – 6)
a = -5 m/s²
Logo, substituindo o valor encontrado:
µ = -a / g
µ = -(-5) / 10
µ = 0,5
Item (b)
Sabemos que trabalho está relacionado ao gasto de energia ao se aplicar uma força produzindo um
deslocamento. Porém, como a única força que atua na direção do deslocamento é a força de atrito,
devemos ter um trabalho resistente (portanto, negativo). Assim:
T = F·∆S·cos θ
T = FAT·∆S·cos 180°
Do gráfico podemos usar a área triângulo formado como numericamente igual ao deslocamento.
Assim
∆S = (b·h)/2
∆S = (2·10)/2
∆S = 10 m
Logo,
T = FAT·∆S·cos 180°
T = (m·a)·∆S·cos 180°
T = (-5·600)·(10)·(-1)
T = 3,00x104 J
2. Na brincadeira conhecida como cabo-de-guerra, dois grupos de palhaços utilizam uma corda ideal que apresenta um nó
no seu ponto mediano. O gráfico abaixo mostra a variação da intensidade da resultante F das forças aplicadas sobre o nó,
em função da sua posição x.
Considere que a força resultante e o deslocamento sejam paralelos.
Determine o trabalho realizado por F no deslocamento entre 2,0 e 9,0m.
Resolução:
Dados:
Todas as informações podem ser extraídas diretamente do gráfico. Assim:
N
T = A1 + A 2
(B + b) ⋅ h b ⋅ h
+
2
2
( 6 + 4) ⋅ 40 1 ⋅ ( −20)
T=
+
2
2
400 ( −20 )
T=
+
2
2
N
T=
A1
A2
T = 190 J
3. A relação entre calor e outras formas de energia foi objeto de intensos estudos durante a Revolução Industrial, e uma
experiência realizada por James P. Joule foi imortalizada. Com ela, ficou demonstrado que o trabalho mecânico e o calor
são duas formas diferentes de energia e que o trabalho mecânico poderia ser convertido em energia térmica. A figura
apresenta uma versão atualizada da máquina de Joule. Um corpo de massa 2 kg é suspenso por um fio cuidadosamente
enrolado em um carretel, ligado ao eixo de um gerador.
O gerador converte a energia mecânica do corpo em elétrica e alimenta um resistor
imerso em um recipiente com água. Suponha que, até que o corpo chegue ao solo,
depois de abandonado a partir do repouso, sejam transferidos para a água 24 J de
energia térmica. Sabendo que esse valor corresponde a 80% da energia mecânica, de
2
qual altura em relação ao solo o corpo foi abandonado? Adote g = 10 m/s .
Resolução:
Dados:
m = 2 kg;
∆E80% = EMEC-80% =24 J;
g = 10 m/s²;
h=?
Sabendo que 24 J equivale a 80% do total da energia mecânica, aplicando “regra de três” verificamos que essa
energia vale 30 J
(J)
(%)
24 ------ 80
EMEC ---100
EMEC = 30 J
Mas como EMEC = EPOT + ECIN e que toda energia cinética será transferida em energia potencial, temos que:
EMEC = EPOT
30 = 2·10·h
h = 1,5 m
4. Sob a ação de uma força constante, um corpo de massa m = 4,0kg adquire, a partir do repouso, a velocidade de 10 m/s.
a) Qual é o trabalho realizado por essa força?
b) Se o corpo se deslocou 25 m, qual o valor da força aplicada?
Resolução:
Dados:
m = 4,0 kg;
v0 = 0 (repouso);
v = 10 m/s;
∆S = 25 m.
Item (a)
Sabemos que
T = ∆ECIN
T = ECINFINAL − ECININICIAL
T=
m ⋅ v² m ⋅ v0 ²
−
2
2
4 ⋅ 10²
T=
2
T = 200 J
T = 2,0x10² J
Item (b)
T = F·∆S
200 = F·25
F = 8,0 N
5. Avalia-se que um atleta de 60kg, numa prova de 10000m rasos, desenvolve uma potência média de 300W.
a) Qual o consumo médio de calorias desse atleta, sabendo que o tempo dessa prova é de cerca de 0,50h?
Dado: 1 cal = 4,2 J.
b) Admita que a velocidade do atleta é constante. Qual a intensidade média da força exercida sobre o atleta durante a
corrida?
Resolução:
Dados:
m = 60 kg;
∆S = 10000 m;
P = 300 W;
∆t = 0,50 h ⇒ ∆t = 1800 s;
1 cal = 4,2 J
Item (a)
Sabemos que
Item (b)
Sabemos que
∆E
∆t
∆E
300 =
1800
∆E = 540000 J
(J)
(cal)
4,2
−
1
540000 −
T
P=
4
T = 1,3x10 J
T = ∆E
T = F·∆S
54x104 = F·104
F = 54 N