Cap1. Funções Reais de Variável Real - Parte 1

Cap1. Funções Reais de variável Real
MatemáticaI – Gestão
ESTG/IPB
Departamento de Matemática
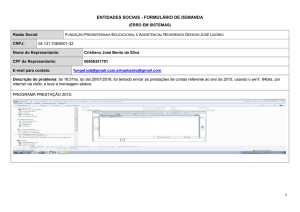
11. Conjuntos de Números
  1, 2,3
Números Naturais
   , 2, 1, 0,1, 2,
Números Inteiros
a

   : a, b  , b  0 
b

    Irracionais
Números Racionais
Números Reais



Irracionais

Alguma notação normalmente usada
  1, 2,
 0  0,1, 2,
   , 2, 1, 0,1, 2,
   1, 2,
a

   : a, b  , b  0 
b

 0   , 2, 1, 0
  x   : x  0
12. Intervalos de Números Reais
Intervalo fechado
2x5
2
ESTG/IPB Departamento de Matemática
ou
x   2,5 
5
Mário Abrantes
http://www.ipb.pt/~mar
28
Matemática I - Gestão
Cap1
ESTG/IPB
Intervalo aberto
2x5
ou
x  2,5
2x5
ou
x  2,5
5
2
Intervalos semiabertos
5
2
2x5
ou
x   2,5
5
2
Exercícios
Representar geometricamente os seguintes intervalos.
(a)
(b)
x  
2  x  e
(c)
x
32
28
13. Funções Reais de Variável Real
Domínio,
Contradomínio, Imagem, Gráfico.
Exemplo (função)
B
A
f
4
1
5
2
6
3
f(1)=4
f(2)=5
f(3)=5
ESTG/IPB Departamento de Matemática
Mário Abrantes
http://www.ipb.pt/~mar
29
Matemática I - Gestão
Cap1
ESTG/IPB
30
Uma função é definida por três entidades: o domínio A, o contradomínio B e uma regra
que associa aos elementos do domínio os elementos do contradomínio. Geralmente as
funções designam-se por letras minúsculas (f no exemplo anterior), e a notação f(1)=4
significa que ao objecto 1 está associada, via função f, a imagem 4.
Designa-se por imagem de f o conjunto de elementos do contradomínio que são
imagens de elementos do domínio – se o domínio é A, a imagem de f representa-se
por f(A); no exemplo anterior temos f ( A)  4,5 . Para indicar que uma função f tem
domínio A e contradomínio B, escreve-se f : A  B .
Chamamos gráfico da função ao conjunto dos pares ordenados  x, f ( x )  , obtidos para
todos os valores x do domínio da função. No caso do exemplo anterior o gráfico da
função é 1, 4  ,  2, 5  ,  3,5  .
Uma relação de um conjunto A para um conjunto B, A  B , define uma função sse a
cada elemento do conjunto de partida, A, corresponde um e um só elemento do
conjunto de chegada, B. A relação g definida no exemplo seguinte não é uma função,
porque existe um elemento no conjunto de partida, 2, ao qual corresponde mais do
que um elemento no conjunto de chegada, 4 e 5.1
Exemplo (a relação g não representa uma função)
B
A
g
1
4
2
5
3
6
Nas funções que vamos utilizar no nosso curso, a regra de associação utilizada é
geralmente expressa por uma fórmula matemática.
1
Em certos contextos considera-se que uma relação como g representa aquilo que se chama uma
função multívoca (cada objecto pode ser associado a mais do que uma imagem). No nosso curso não
usaremos esta definição de função.
ESTG/IPB Departamento de Matemática
Mário Abrantes
http://www.ipb.pt/~mar
Matemática I - Gestão
Cap1
ESTG/IPB
31
Exemplo
A função f :    , f ( x)  2 x , é uma função que a cada objecto x do domínio
associa o seu dobro, 2x , como imagem. Para efeitos de representação gráfica, e
também por simplicidade, costuma escrever-se y  2 x em vez de f ( x)  2 x . A letra
x designa-se por variável independente e y designa-se por variável dependente (o
seu valor depende do valor atribuído a x ). Na representação do gráfico desta
função, os valores da variável x marcam-se no eixo dos xx e os da variável y
marcam-se no eixo dos yy . Dois pontos são suficientes para representar o gráfico,
uma vez que a função corresponde a uma recta.
y
1, 2 
 0, 0 
x  0  y  2 0  0
x
x  1  y  2 1  2
A expressão função real de variável real significa que na expressão f ( x)  x tanto x
como f ( x) tomam valores reais.
14. Funções Elementares
Nesta secção vamos estudar um conjunto de funções designadas de funções
elementares. São deste tipo a maioria das funções que vamos utilizar no nosso curso.
O conjunto das funções elementares contém um núcleo de funções, ditas funções
elementares principais, sendo as restantes funções elementares construídas por meio
de um número finito de operações elementares efectuadas sobre as funções principais.
As operações elementares são: adição, subtracção, multiplicação, divisão e
composição.
Apresentam-se de seguida as funções elementares principais.
Funções Elementares Principais
1) Função Constante
Forma geral:
ESTG/IPB Departamento de Matemática
y  k, k  
Mário Abrantes
http://www.ipb.pt/~mar
Matemática I - Gestão
Cap1
ESTG/IPB
Representação do Gráfico
k
Exemplos:
y  3 , y  3 22
2) Função Potência
y  xk , k  
Forma geral:
3
Exemplos:
y  x 3 , y  x 2 , y  x 2
Representação do Gráfico
(gráficos retirados deste site)
ESTG/IPB Departamento de Matemática
Mário Abrantes
http://www.ipb.pt/~mar
32
Matemática I - Gestão
Cap1
ESTG/IPB
(gráfico retirado deste site)
(gráfico retirado deste site)
3) Função Exponencial
y  a x , a  1, a  0
Forma geral:
Exemplos:
y  e x , y  0.1x , y  2 x
Representação do Gráfico
(gráfico retirado deste site)
ESTG/IPB Departamento de Matemática
Mário Abrantes
http://www.ipb.pt/~mar
33
Matemática I - Gestão
Cap1
ESTG/IPB
34
4) Função Logaritmo
Forma geral:
Exemplos:
y  log a x, a  1, a  0
y  log 3 x , y  log 0.1 x , y  log e x
Representação do Gráfico
(gráfico retirado deste site)
5) Funções Trigonométricas Directas e Inversas
Directas:
y  sen( x), y  cos( x), y  tg ( x), y  cotg ( x), y  sec( x), y  cos ec( x)
Inversas:
y  arcsen( x ), y  arc cos( x ), y  arctg ( x), y  arccotg ( x ),
y  arc sec( x ), y  arc cos ec ( x)
ESTG/IPB Departamento de Matemática
Mário Abrantes
http://www.ipb.pt/~mar
Matemática I - Gestão
Cap1
ESTG/IPB
35
Representação do Gráfico
(gráfico retirado deste site)
sen    
B
C
seno de 
cos    
A
C
coseno de 
C
B

A
tg    
sen   
cos   
cotg    
sec    
cos   
sen   
Mário Abrantes
B
A

tangente de 
A
B
1
C

cos    A
cos ec    
ESTG/IPB Departamento de Matemática

1
C

sen    B
cotangente de 
secante de 
cosecante de 
http://www.ipb.pt/~mar
Matemática I - Gestão
Cap1
ESTG/IPB
36
Decomposição de Funções em Combinações de Funções Elementares Principais
Uma função diz-se elementar sse:
(a) É uma função elementar principal;
(b) É obtida combinando funções elementares principais, por meio de um
número finito de operações de adição, subtracção, divisão, multiplicação e
composição.
A cada função elementar corresponde sempre uma só fórmula
Exemplos
1.
f ( x)  x  2 é uma função elementar (FE), dado que é uma soma das
funções elementares principais (FEP)
f 2 ( x)  2
f1 ( x)  x (função potência) e
(função constante). O seguinte esquema representa a
decomposição de f ( x) numa soma de FEPs.
f ( x)  x  2

f1 ( x)  x
f 2 ( x)  2
f ( x)  f1 ( x)  f 2 ( x)
2. A função módulo, f ( x)  x , é uma FE. Embora na sua definição normal lhe
sejam associadas duas fórmulas
  x, x  0
,
x 
x0
 x,
esta função pode ser definida por meio da fórmula única x  x 2 , que
resulta da composição das FEPs
f1 ( x )  x (função potência) e f1 ( x )  x 2
(função potência),
x  f1  f 2 ( x )  .
ESTG/IPB Departamento de Matemática
Mário Abrantes
http://www.ipb.pt/~mar
Matemática I - Gestão
Cap1
ESTG/IPB
37
Exercícios
Mostrar que as seguintes são FEs.
(a) f ( x ) 
x 1
x 1
 x 1 

 x 1 
(b) f ( x)  sen 
x
(c) f ( x)  e  2
Resolução
f ( x ) é FE porque pode ser decomposta em FEPs como a seguir se mostra.
(a)
f ( x) 

x 1
f1 ( x)  x

x 1
f2 ( x)  1
f1 ( x)  x
f ( x) 
(b)
x 1
x 1

f2 ( x)  1
f1 ( x )  f 2 ( x )
f1 ( x )  f 2 ( x )
f ( x ) é FE porque é a composição da FEP f1 ( x)  sen( x) e da FE f 2 ( x ) 
x 1
:
x 1
f ( x )  f1  f 2  x  
ESTG/IPB Departamento de Matemática
Mário Abrantes
http://www.ipb.pt/~mar
Matemática I - Gestão
(c)
Cap1
ESTG/IPB
38
f ( x ) é FE porque pode ser decomposta em FEs como a seguir se mostra.
Anteriormente já se mostrou que f3 ( x)  x é FE.
x
f ( x)  e  2
e
f2 ( x)  e x


x
f1 ( x)  2
f3 ( x)  x
f ( x)  f 2  f3 ( x)   f1 ( x)
Proposição
Se f ( x ) , g( x ) são duas funções elementares e f  0   g  0  , então a função
 f ( x ), x  0
h( x )  
 g( x ), x  0
é também uma função elementar.
Prova
A função h( x ) pode ser escrita com uma só fórmula (verificar),
 x x
 x x
h( x )  f  
 g
  g 0 .
2 

 2 
 x x
Esta função é elementar porque é obtida combinando as funções f  
 , que é
2


elementar porque é a composição das FEs f  x  e 
ESTG/IPB Departamento de Matemática
Mário Abrantes
x x
2
 x x
 , que é
 2 
; g
http://www.ipb.pt/~mar
Matemática I - Gestão
Cap1
elementar porque é a composição das FEs g  x  e
x x
2
ESTG/IPB
39
;  g  0  , que é elementar por
ser uma constante. 
Exemplo
1, x  0
A função h( x )   x
é elementar.
e
,
x

0

Usando a demonstração da proposição anterior, podemos escrever,
fazendo f  x   1 e g  x   e x ,
 x x
 x x
h( x )  f  
 g
  g 0
2 

 2 
x x
 1 e
2
x x
1  e
2
Um resultado que generaliza o anterior é o seguinte.
Proposição
Se f ( x ) , g( x ) são duas funções elementares e f ( a )  g( a ) , então a função
 f ( x ), x  a
h( x )  
 g( x ), x  a
é também uma função elementar.
Prova
A função h( x ) pode ser escrita com uma só fórmula (verificar),
 x  a   x  a

 x  a   x  a

h( x )  f  
 a  g 
 a   g a ,
2
2




que é uma função é elementar. 
Se substituirmos a por zero nesta expressão, obtemos a expressão da proposição
anterior, mostrando que aquela é um caso particular da acima apresentada.
ESTG/IPB Departamento de Matemática
Mário Abrantes
http://www.ipb.pt/~mar
Matemática I - Gestão
Cap1
ESTG/IPB
Exemplo
x 1
 x,
A função h( x )  
é elementar.
ln  x   1, x  1
Usando a demonstração da proposição anterior, podemos escrever, fazendo
f  x   x e g  x   ln  x   1 ,
 x  1   x  1 
 x  1   x  1 
h( x )  f  
 1  g 
 1  g 1
2
2




x  1   x  1
 x  1   x  1 

 1  ln 
 1  1
2
2



x  1   x  1
 x  1   x  1 
 ln 
 1
2
2


que é uma função elementar.
Outro resultado interessante é o que segue.
Proposição (aqui)
Se f ( x ) , g( x ) são duas funções elementares, então a função
 f ( x ), x  a
h( x )  
 g( x ), x  a
é também uma função elementar.
Prova
A função h( x ) pode definir-se recorrendo à fórmula (verificar)
h( x )  f ( x )
x  a ( x  a )
2 xa
 g( x )
x  a ( x  a )
2( x  a )
.
h( x ) é função elementar por ser obtida combinando funções elementares. 
ESTG/IPB Departamento de Matemática
Mário Abrantes
http://www.ipb.pt/~mar
40
Matemática I - Gestão
Cap1
ESTG/IPB
41
A seguir apresenta-se um tipo de função definida por ramos, que não é elementar.
Proposição
Se f ( x ) , g( x ) são duas funções elementares e se f ( a )  g( a ) , então a
função
 f  x  , x  a
h  x  
 g  x  , x  a
não é uma função elementar.
Prova
Como veremos na secção sobre continuidade de funções, a função h( x ) tem uma
descontinuidade de 1ª espécie no ponto x  a . Nenhuma função elementar principal
tem descontinuidades deste tipo; se adicionarmos, subtrairmos, multiplicarmos,
dividirmos ou compusermos duas funções que não tenham descontinuidades deste
tipo, então a função resultante também não tem. h  x  não pode ser função
elementar. 
Exemplo
2, x  0
A função h  x   
não é elementar.
3
,
x

0

3
2
ESTG/IPB Departamento de Matemática
Mário Abrantes
http://www.ipb.pt/~mar