Apontamentos de Aritmética.

Matemática I - Gestão 2012/13
Aritmética
p1
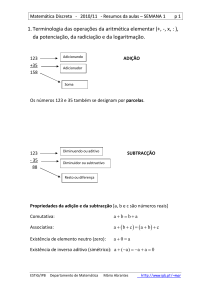
1. Terminologia das operações da aritmética elementar (+, -, x, : ),
da potenciação, da radiciação e da logaritmação.
Adicionando
123
+35
158
ADIÇÃO
Adicionador
o
Soma
Os números 123 e 35 também se designam por parcelas.
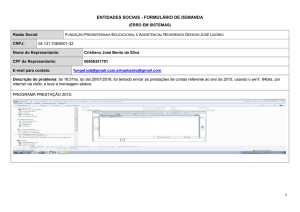
Diminuendo ou aditivo
123
- 35
88
SUBTRACÇÃO
Diminuidor ou subtractivo
Resto ou diferença
Propriedades da adição e da subtracção [a, b e c são números reais]
Comutativa:
abba
Associativa:
a   b  c  a  b  c
Existência de elemento neutro (zero):
a0a
Existência de inverso aditivo (simétrico): a  (a)  a  a  0
ESTiG/IPB
Departamento de Matemática
Mário Abrantes
http://www.ipb.pt/~mar
Matemática I - Gestão 2012/13
Aritmética
Multiplicando
23
x35
115
69_
805
p2
MULTIPLICAÇÃO
Multiplicador
Produto
Os números 23 e 35 também se designam por factores.
Dividendo
127.00 |4___
-12
31,75
07
-4
30
-28
20
-20
0
Divisor
Quociente
DIVISÃO
Resto
Propriedades da Multiplicação [a, b e c são números reais]
Comutativa:
a b  ba
Associativa:
a   b  c  a  b  c
Existência de elemento neutro (unidade):
a 1  a
Existência de inverso multiplicativo:
1
a  1
a
ESTiG/IPB
Departamento de Matemática
Mário Abrantes
http://www.ipb.pt/~mar
Matemática I - Gestão 2012/13
Aritmética
p3
Sinal de radical
3
64  4
Raiz
RADICIAÇÃO
Radicando: número não-negativo se o índice é par ; de
contrário temos que trabalhar com números complexos
Índice do radical: número inteiro positivo
Lê-se “Raiz índice 3 de 64” ou “Raiz cúbica de 64”.
A raiz índice n de um número positivo b é a única solução positiva da
equação x n  b .
Propriedades da Radiciação [a, b são números reais não negativos; n, m
são números inteiros não negativos]
n
ab  n a n b
n
a na

, b0
b nb
n
am 
n m
 
n
m
a
a  nm a
Se o radicando b for negativo o índice n da raiz
ESTiG/IPB
Departamento de Matemática
n
Mário Abrantes
b tem que ser ímpar.
http://www.ipb.pt/~mar
Matemática I - Gestão 2012/13
3
4  64
Aritmética
p4
Expoente
POTENCIAÇÃO
Base
Propriedades da Potenciação
1. a n a m  a n  m
an
2. m  a n m , a  0
a
1
3. a  n  n , a  0 , consequência de 2.
a
0
4. a  1 , consequência de 2.
m
n
m
 n1 
n m
Nota: por definição temos a  a   a  , sendo n e a positivos.
 
log 2 32  5
Logaritmando: número positivo
Base do logaritmo: número
positivo
LOGARITMAÇÃO
Lê-se “Logaritmo de 32 na base 2”.
ESTiG/IPB
Departamento de Matemática
Mário Abrantes
http://www.ipb.pt/~mar
Matemática I - Gestão 2012/13
Aritmética
p5
O logaritmo na base b de um número positivo c é a única solução da
equação b x  c .
Propriedades da Logaritmação
1. log a  b  c   loga b  log a c
b
 log a b  log a c, c  0
c
3. log a bc  c  log a b
2. log a
4. a loga b  b
----------------------------------------------------------------------------------------------
2.Fracções
a
b
Numerador
Denominador
Operações com fracções
a c ad  bc
 
b d
bd
a c ac
 
b d bd
a c a d
  
b d b c
n
an
a
   n
b
b
ESTiG/IPB
Departamento de Matemática
Mário Abrantes
http://www.ipb.pt/~mar
Matemática I - Gestão 2012/13
Aritmética
p6
Conjuntos de Números
Números naturais: N  1,2,3,
Números inteiros:   , 2, 1,0,1,2,
a

Números racionais: Q   : a,b  Z; b  0 
b

Números reais: R  Q  números irracionais
Um número diz-se irracional se não pode ser escrito como uma fracção.
Exemplos de números irracionais:
2, e,  .
ESTiG/IPB
Mário Abrantes
Departamento de Matemática
http://www.ipb.pt/~mar