primeira lei da termodinâmica - intermediário

PRIMEIRA LEI DA TERMODINÂMICA - INTERMEDIÁRIO
Exercícios Resolvidos
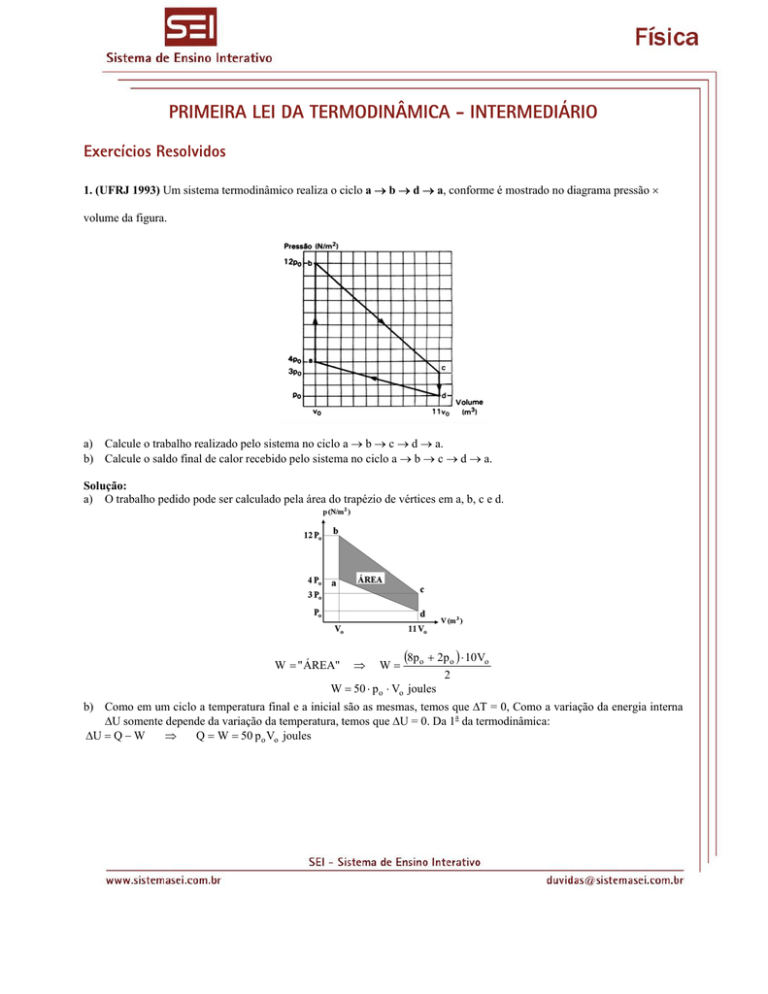
1. (UFRJ 1993) Um sistema termodinâmico realiza o ciclo a → b → d → a, conforme é mostrado no diagrama pressão ×
volume da figura.
a) Calcule o trabalho realizado pelo sistema no ciclo a → b → c → d → a.
b) Calcule o saldo final de calor recebido pelo sistema no ciclo a → b → c → d → a.
Solução:
a) O trabalho pedido pode ser calculado pela área do trapézio de vértices em a, b, c e d.
W = " ÁREA"
⇒
W=
(8p o + 2p o ) ⋅ 10Vo
2
W = 50 ⋅ p o ⋅ Vo joules
b) Como em um ciclo a temperatura final e a inicial são as mesmas, temos que ΔT = 0, Como a variação da energia interna
ΔU somente depende da variação da temperatura, temos que ΔU = 0. Da 1a da termodinâmica:
ΔU = Q − W
⇒
Q = W = 50 p o Vo joules
2. (UFRJ 2009) Um gás ideal se encontra em um estado de equilíbrio termodinâmico A no qual tem volume V0 e pressão p0
conhecidos. O gás é então comprimido lentamente até atingir um estado de equilíbrio termodinâmico B no qual seu volume é
V0 / 3.
Sabendo que o processo que leva o gás do estado A ao estado B é o indicado pelo segmento de reta do diagrama, e que os
estados A e B estão em uma mesma isoterma, calcule o calor total QAB cedido pelo gás nesse processo.
Solução:
Como os estados A e B do gás ideal estão à mesma temperatura, a energia interna de ambos é a mesma. Portanto, pela
Primeira Lei da Termodinâmica (ΔU = Q – W), no processo considerado de A até B, o calor recebido pelo gás é igual ao
trabalho que ele realiza. O trabalho realizado é WAB = (1/2)(pB + pA) (VB − VA), ou seja, WAB = (1/2)(pB + p0) (−2V0 /3). Mas,
pela lei dos gases ideais, pB(V0/3) = p0V0, isto é, pB = 3p0; logo, WAB = (1/2)(3p0 + p0) (−2V0/3), isto é, WAB = − 4p0V0 / 3.
Portanto, o calor recebido pelo gás no processo é − 4p0V0/3 e, conseqüentemente, o calor cedido pelo gás nesse processo é
QAB = 4p0V0/3.
Exercícios Propostos
1. (IME 1999-2000) Um cilindro contém oxigênio à pressão de 2 atmosferas e ocupa um volume de 3 litros à
temperatura de 300 K. O gás, cujo comportamento é considerado ideal, executa um ciclo termodinâmico através dos
seguintes processos:
Processo 1-2: aquecimento a pressão constante até 500 K.
Processo 2-3: resfriamento a volume constante até 250 K.
Processo 3-4: resfriamento a pressão constante até 150 K.
Processo 4-1: aquecimento a volume constante até 300 K.
Ilustre os processos em um diagrama pressão-volume e determine o trabalho executado pelo gás, em Joules, durante o
ciclo descrito acima. Determine, ainda, o calor líquido produzido ao longo deste ciclo.
Dado: 1 atm = 105 Pa.
2. (ITA 2009) Três processos compõem o ciclo termodinâmico ABCA mostrado no diagrama P x V da figura.
O processo AB ocorre a temperatura constante. O processo BC ocorre a volume constante com decréscimo de 40 J de energia
interna e, no processo CA, adiabático, um trabalho de 40 J é efetuado sobre o sistema. Sabendo-se também que em um ciclo
completo o trabalho total realizado pelo sistema é de 30 J, calcule a quantidade de calor trocado durante o processo AB.
3. (IME 1994_1995) Um tanque rígido contém um determinado gás a uma temperatura de 300 K. Durante o seu
transporte o tanque fica exposto a uma incidência de energia solar absorvendo 40 KJ/h. Considerando um período de
três horas de exposição, determine:
a) O trabalho realizado pelo gás. Justifique sua resposta.
b) A temperatura final do gás.
Dado: Capacidade térmica do gás: 2KJ/K.
4. (UFRJ 2003) Um gás ideal realizou um ciclo termodinâmico ABCDA, ilustrado na figura.
a) Calcule o trabalho total realizado pelo gás no ciclo.
b) Aplicando a 1a Lei da Termodinâmica ao gás no ciclo e adotando a convenção de que o calor absorvido é positivo e o calor
cedido é negativo, investigue a soma do calor trocado nas diagonais, isto é, QBC+QDA, e conclua se esta soma é maior, igual ou
menor que zero. Justifique sua resposta.
Respostas
1.
τ = 200J. Q = 200 J (Q > 0. Logo, trata-se de um calor absorvido durante o ciclo)
2.
QAB = 70 J
3.
a) W = 0. O tanque é rígido, logo, seu volume não varia.
b) T = 360K
4.
⎛ p + p0 ⎞
a) o trabalho realizado no trecho ABC é igual à área do trapézio: ⎜ 1
⎟(V1 − V0 ) .
⎝ 2 ⎠
O trabalho realizado no trecho CDA é igual à mesma área, mas com sinal trocado.
Assim Wtotal = 0
b) Pela 1ª Lei da Termodinâmica
ΔU=Q-W e no ciclo fechado Δ U=0, logo
QAB+QBC+QCD+QDA=0
Nos processos: AB QAB=ΔUAD>0 pois TB>TA
CD QCD=ΔUCD>0 pois TD>TC
Logo QBC + QCD < 0
A Equipe SEI recomenda que, após a conclusão dos exercícios propostos, o aluno tente os exercícios de nível avançado
deste assunto. Os outros artigos estão disponíveis no nosso site.