P4 - PROVA DE QUÍMICA GERAL

P4 - PROVA DE QUÍMICA GERAL - 05/12/07
Nome:
GABARITO
Nº de Matrícula:
Turma:
Assinatura:
Questão
Valor
1a
2,5
2a
2,5
3a
2,5
4a
2,5
Total
10,0
Constantes e equações:
R = 0,082 atm L mol-1 K-1 = 8,314 J mol-1 K-1
G = Go + R T ln Q
Go = Ho - T So
[A] = [A]0 – kt
1
1
=
+ kt
[A] [A]0
ln
[A]
= kt
[A]0
!E = !E°
RT
lnQ
nF
Grau
Revisão
1a Questão
Uma pilha eletroquímica é montada com dois eletrodos: o primeiro constituído por
um fio de prata imerso em uma solução aquosa contendo íons Ag+ e o segundo,
constituído por um fio de platina imerso em uma solução aquosa contendo íons
Fe2+ e Fe3+. Pergunta-se:
a) Qual é a reação global da pilha nas condições-padrão?
b) Calcule E° para essa pilha.
c) Calcule
E da pilha quando a concentração de Ag+ for 0,1 mol L-1 e as
concentrações de Fe2+ e Fe3+ forem ambas 1,0 mol L-1, a 25°C.
d) Nas condições do item (c), a direção da reação global continua sendo a mesma
do item (a)? Explique.
Dados: a 25 °C:
Ag+(aq) + eFe3+(aq) + e-
Ag(s)
E° = +0,80V
Fe2+(aq) E° = +0,77V
Resolução:
a) Anodo: Fe2+(aq)
Fe3+(aq) + e- ; 0,77V
Catodo: Ag+(aq) + eAg+(aq) + Fe2+(aq)
b)
Ag(s)
; 0,80V
Ag(s)+ Fe3+(aq) ; 0,03 V
E° = 0,03 V
c) !E = !E°
RT
lnQ
nF
E = 0,03 -
d) Não. Passa a ser eletrólise.
0,0592
1
log
1
1 x 0,1
E = - 0,03V
2a Questão
A água dissocia-se conforme a reação abaixo:
2H2O(l)
H3O+(aq) + OH-(aq)
!Ho = 55,9 kJ ; !So = -80,5 J K-1; Kw = 1,0 x 10-14
a) Identifique os dois pares ácido-base conjugados desta dissociação segundo o
conceito de Bronsted–Lowry.
b) Calcule o valor de !Go, em kJ, para a dissociação da água, a 25 °C, e comente
o resultado obtido.
c) Qual é o valor do !G, em kJ, para a dissociação da água pura, ou seja, quando
ela for uma solução neutra, a 25oC? Justifique.
d) Comente a respeito da espontaneidade das reações de neutralização entre um
ácido forte e uma base forte (representada abaixo) com a variação de
temperatura.
H3O+(aq) + OH-(aq)
2H2O(l)
Resolução:
a)
H2O
OH
e
H3 O +
H2 O
b) Duas maneiras
b.1) G° = H° - T S°
G° = 55,9 – 298 x (-0,0805)
G° = + 79,9 kJ
b.2)
G° = - R T ln kw
Go = - 8,314 x 10-3 . 298 ln (1,0x 10-14)
Go + 79,9 kJ
c) G = 0 no equilíbrio
G = Go + R T ln Q
G = 79,9 + 8,314 x 10-3 . 298 ln (1,00x 10-14)
G=0
d) G° =
79,9 ;
S° =
80,5 ;
H° =
55,9
A reação de neutralização é espontânea em todas as temperaturas.
3a Questão
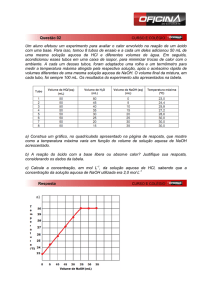
Considere a decomposição da amônia, NH3, em um reator de 10 L e o respectivo
gráfico que mostra a variação da concentração do NH3 (em milimol por litro) em
função do tempo de reação (em segundos), a 300 0C.
2NH3(g)
N2(g) + 3H2(g)
2,2
2,0
1,8
[NH3] em mmol L
-1
1,6
1,4
1,2
1,0
0,8
0,6
0,4
0,2
0,0
0
100
200
300
400
500
600
Tempo (s)
a) Escreva a lei de velocidade da reação indicando o valor numérico da constante
de velocidade.
b) Calcule a pressão total no reator após 1000 s de reação.
Resolução:
a) Quando a variação da concentração de NH3 em função do tempo se comporta
de forma linear com inclinação negativa tem-se que a reação de decomposição
em questão é um processo de ordem zero. Logo, a lei de velocidade assume a
forma:
v = k[NH3]0 = k
O valor de k é obtido da inclinação da curva, ou seja:
k = ![NH3]/!t = (2,1 – 1,2) x 10-3 mol L-1/ (600 – 0) s = 1,5 x 10-6 mol L-1 s-1
Assim: v = 1,5 x 10-6
b) A pressão total do sistema será dada pela lei de Dalton, considerando a
pressão parcial de NH3 após 1000 s de reação e as pressões parciais dos
produtos N2 e de H2:
Ptotal = PNH3 + PN2 + PH2
Onde P = nRT/V = [ ]RT
Após 1000s de reação, a concentração de NH3 restante é calculada pela equação
integrada:
[NH3]1000 = [NH3]0 – kt
O valor de [NH3]0 é obtido pelo coeficiente linear do gráfico, ou seja 2,1 x 10-3
mol/L-1
Logo:
[NH3]1000 = 2,1 x 10-3 mol/L-1 – 1,5 x 10-6 mol L-1 s-1 x 1000 s = 6 x 10-4 mol/L-1
Considerando a estequiometria da reação:
0 s:
1000 s:
mol/L-1
Assim:
NH3
2,1 x 10-3 mol/L-1
6,0 x 10-4 mol/L-1
N2
H2
0 mol/L-1
0 mol/L-1
-4
7,5 x 10 mol/L-1 2,25
x
10-4
Ptotal = ([NH3]1000 + [N2]1000 + [H2]1000) x RT
Ptotal = (6,0 x 10-4 + 7,5 x 10-4 + 2,25 x 10-3) mol/L-1 x 0.082 atm L mol-1 K-1 x 598 K
Ptotal = 0,18 atm.
4a Questão
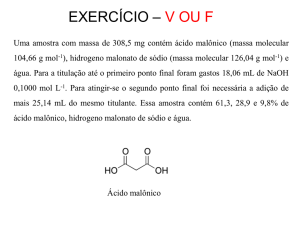
Em um laboratório havia um frasco com ácido sulfúrico. Este frasco estava com o
rótulo deteriorado e, além do nome do produto, lia-se apenas sua densidade:
1,728 g mL-1. Um volume de 10 mL deste ácido foi diluído para 500 mL. Uma
amostra de 25 mL da solução diluída foi reagido completa e estequiometricamente
com 20,03 mL de uma solução de NaOH de concentração 27,28 g L-1 . Pede-se:
H2SO4(aq) + 2NaOH(aq)
Na2SO4(aq) + 2H2O(l)
a) A concentração, em mol L-1, no frasco de ácido sulfúrico.
b) A porcentagem de ácido sulfúrico, em massa, no frasco original.
c) O pH da solução ácida formada após a diluição para 500 mL, antes da
neutralização.
H2SO4(aq)
2H+(aq) + SO42-(aq)
Resolução:
a) 27,28 g
1000 mL NaOH
x
20,23 mL
x
0,5519 g
n NaOH =
0,5519g
= 0,01380 mol NaOH
40g/mol
1H2SO 4
2NaOH
x
0,01380
0,006898
25mL
x
500 mL
x = 0,006898 mol H2SO 4 na amostra de 25mL
x = 0,1380 mol H2SO 4 na solução 500mL e igual quantidade
na amostra de 10mL
0,1380 mol 10 mL
x = 13,80 mol L-1 H2SO 4
x
1000 mL
b)
1,728 g
x
1L
1mL
x = 1728 g de solução H2SO 4
1000 mL
13,80 mol =
m(g)
98
m(g) = 1352 g de H2SO 4
1728 g 100%
x = 78,25%
1352 X
c)
2H+(aq)
H2SO4
0,1380mol
0,5L
0,276
2x
0,1380mol
0,5L
2 x 0,276
pH = -log [H+] = -log (2 x 0,276) = 0,26
+
SO42-(aq)
0,1380mol
0,5L
0,276