função de 2º grau - Professor Joaquim

Prof. Joaquim Rodrigues
FUNÇÃO DE 2º GRAU
A função de 2º grau, ou função quadrática é aquela que possui a forma
f ( x) = a x 2 + bx + c , com a, b e c reais e a ≠ 0. Tem uma grande aplicação prática,
principalmente no cálculo de maximização e minimização.
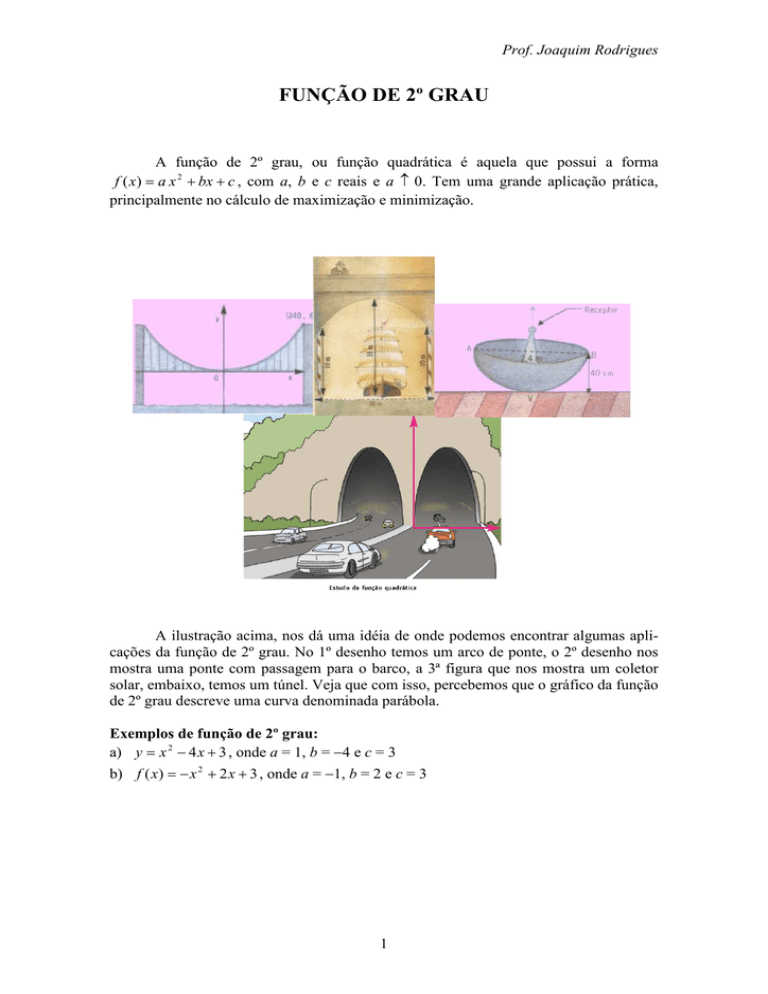
A ilustração acima, nos dá uma idéia de onde podemos encontrar algumas aplicações da função de 2º grau. No 1º desenho temos um arco de ponte, o 2º desenho nos
mostra uma ponte com passagem para o barco, a 3ª figura que nos mostra um coletor
solar, embaixo, temos um túnel. Veja que com isso, percebemos que o gráfico da função
de 2º grau descreve uma curva denominada parábola.
Exemplos de função de 2º grau:
a) y = x 2 − 4 x + 3 , onde a = 1, b = −4 e c = 3
b) f ( x) = − x 2 + 2 x + 3 , onde a = −1, b = 2 e c = 3
1
Prof. Joaquim Rodrigues
CÁLCULO DOS ZEROS DA FUNÇÃO QUADRÁTICA
Denomina-se zero ou raiz da função f ( x) = a x 2 + bx + c , o valor de x que anula a função, isto é f ( x) = 0 .
Exemplos:
Calcule os zeros (ou raízes) da função:
a) y = x 2 − 4 x + 3
Basta igualar a função f(x) a zero, daí temos:
x 2 − 4 x + 3 = 0 (agora temos uma equação de 2º grau, que pode ser resolvida pela
fórmula de Bháskara)
−b± ∆
a x 2 + bx + c = 0 ⇒ x =
, onde ∆ é chamado de discriminante e é calcu2a
lado por ∆ = b 2 − 4ac .
Note que esse discriminante ∆ é quem vai nos dizer a quantidade de raízes que possui a equação de 2º grau.
Se ∆ > 0 (isto é, positivo, significa que teremos duas raízes reais e diferentes na equação)
Se ∆ = 0 (isto é, nulo, significa que teremos duas raízes reais e iguais, ou uma única
raiz)
Se ∆ < 0 (isto é, negativo, significa que não teremos nenhuma raiz real)
Assim, voltando a nossa equação x 2 − 4 x + 3 = 0 , vamos calcular o valor de ∆
∆ = b 2 − 4ac ⇒ ∆ = (−4) 2 − 4 ⋅ 1 ⋅ 3 = 16 − 12 = 4 , como ∆ = 4 (positivo, então teremos duas raízes reais e diferentes)
−b± ∆
− (−4) ± 4 4 ± 2
4−2 2
x=
⇒
x=
=
⇒
x′ =
= =1
e
2a
2 ⋅1
2
2
2
4+2 6
x ′′ =
= = 3 , logo, as raízes são: 1 e 3.
2
2
b) f ( x) = − x 2 + 2 x + 3
Igualando a função a zero, temos − x 2 + 2 x + 3 = 0 (fica mais fácil fazer as contas,
se multiplicarmos a expressão − x 2 + 2 x + 3 = 0 por −1)
O
que
temos
agora
x 2 − 2x − 3 = 0 ,
calculando
∆ = b 2 − 4ac
∆ = (−2) 2 − 4 ⋅ 1 ⋅ (−3)
∆ = 4 + 12 = 16 , mais uma vez, teremos duas raízes reais e diferentes.
− (−2) ± 16 2 ± 4
2−4 −2
−b± ∆
⇒ x=
=
⇒ x′ =
=
= −1 e
x=
2a
2 ⋅1
2
2
2
2+4 6
x ′′ =
= = 3,
2
2
logo, as raízes são −1 e 3.
2
Prof. Joaquim Rodrigues
c) f ( x) = 5 x 2 + 10 x
Igualando a função a zero, temos 5 x 2 + 10 x = 0 , e podemos notar que a equação de
2º grau que se apresentou é incompleta, pois está faltando o termo c, que neste caso,
será zero.
Fica mais fácil, então, no lugar de usar a fórmula de Bháskara, colocar o x em evidência, assim: 5 x 2 + 10 x = 0 ⇒ x (5 x + 10) = 0 ⇒ x′ = 0 e 5 x + 10 = 0 ⇒
− 10
5 x = −10 ⇒ x =
⇒ x ′′ = −2 , logo, as raízes são 0 e −2.
5
d) f ( x) = x 2 − 4
Igualando a função a zero, temos x 2 − 4 = 0 , e também podemos notar que essa
equação, também é incompleta, pois está faltando o termo b, que neste caso, é zero.
Também fica mais fácil resolver sem usar a fórmula de Bháskara, assim:
x 2 − 4 = 0 ⇒ x 2 = 4 ⇒ x = ± 4 ⇒ x = ±2 , logo, as raízes são −2 e 2.
GRÁFICO
Como vimos, na definição introdutória, o gráfico da função de 2º grau é uma curva denominada parábola, que terá concavidade voltada “para cima” se a > 0 ou voltada “para baixo” se a < 0.
Concavidade voltada para cima (a > 0)
Corta o eixo x em
dois pontos, logo,
temos duas raízes
reais e diferentes,
isto é, ∆ > 0
Corta o eixo x em
um único ponto,
logo, temos uma
única raiz real,
isto é, ∆ = 0
3
Não corta o eixo x,
logo, não temos
raízes reais, isto é,
∆<0
Prof. Joaquim Rodrigues
Concavidade voltada para baixo (a < 0)
Corta o eixo x em
dois pontos, logo,
temos duas raízes
reais e diferentes,
isto é, ∆ > 0
Corta o eixo x em
um único ponto,
logo, temos uma
única raiz real,
isto é, ∆ = 0
Não corta o eixo x,
logo, não temos
raízes reais, isto é,
∆<0
COORDENADAS DO VÉRTICE
Podemos observar que, se a concavidade da parábola, estiver voltada “ para cima” (ou seja a > 0), a parábola apresenta um ponto que é o “mais baixo” (ponto de mínimo da função), mas, se a concavidade estiver voltada “para baixo” (a < 0), então a
parábola apresenta um ponto que é o “mais alto” (ponto de máximo da função). Esse
ponto (mínimo ou máximo) é chamado de vértice V ( xV , yV ) da parábola e suas coorb
∆
denadas são xv = −
e yv = −
, sendo que a reta que contém o vértice da parábola
2a
4a
e é paralela ao eixo y é denominada de eixo de simetria.
a<0
a>0
Eixo de simetria
Eixo de simetria
V (vértice)
V (vértice)
4
Prof. Joaquim Rodrigues
Com esses dados, podemos calcular maximização ou minimização em várias situações:
Exemplo:
O lucro mensal de uma empresa é dado por L( x) = − x 2 + 10 x − 16 , em que x é a quantidade vendida.
a) Para que valores de x, o lucro é nulo, ou seja, não houve lucro?
b) Qual será o valor de x para obtermos o maior lucro possível?
c) Qual é esse maior lucro?
Resolução
a) se queremos saber, para que valor de x o lucro é nulo, basta igualar a função a zero
− x 2 + 10 x − 16 = 0 (−1) ⇒ x 2 − 10 x + 16 = 0 (usando a fórmula de Bháskara, temos) x ′ = 2 e x ′′ = 8 , ou seja, quando para x = 2 ou x = 8
b
(−10) 10
⇒ xv = −
=
= 5 , significa que
b) basta calcular o xv, então temos: xv = −
2a
2 ⋅1
2
quando vender 5 unidades, a empresa terá conseguido seu lucro máximo.
c) agora é só calcular o yv, que nesse caso, fica mais fácil se substituirmos o xv na fun⇒
L(5) = −5 2 + 10 ⋅ 5 − 16
⇒
ção assim, L( x) = − x 2 + 10 x − 16
L(5) = −25 + 50 − 16 = 9 , ou seja, quando a empresa tiver conseguido vender 5 unidades, então terá o seu maior lucro que será de 9 unidades monetárias.
EXERCÍCIOS
Questão 01
Dadas as funções de IR em IR, marque com um X aquelas que são funções de 2º grau:
a) ( ) f ( x) = 3 x 2 − 6 x + 1
b) ( ) y = − x 2 + 4 x
c) (
d) (
e) (
f) (
g) (
) f ( x) = 2 x − 8
) f ( x) = 3 x + 7
5 4
) f ( x) = 2 −
x
x
2
x
5
) y=
−
8 6
3
) f ( x) = 16 − 3
x
Questão 02
Dada a função f ( x) = x 2 − 5 x + 6 , calcule:
a) f(−1)
b) f(0)
c) f(1)
d) f(2)
Questão 03
Calcule os zeros (raízes) de cada função:
a) y = x 2 − 5 x − 24
b) y = 4 x 2 − x + 2
c) f ( x) = x 2 − 6 x + 9
d) f ( x) = x 2 − 9
5
e) f(3)
Prof. Joaquim Rodrigues
Questão 04
Dizer se as funções quadráticas abaixo têm concavidade voltada para cima ou para baixo:
a) y = 2 x 2 − 3 x + 4
b) f ( x) = − x 2 + 6 x − 9
c) f ( x) = x 2
d) f ( x) = −2 x 2 + 16
Questão 05
O valor mínimo de y em y = x 2 − 5 x + 6 é:
a) −0, 25
b) −0, 5
c) 0
d) 2, 5
e) 3, 0
Questão 06
A temperatura, em graus centígrados, no interior de uma câmara, é dada pela função
f ( t ) = t 2 − 7t + A , onde t é medido em minutos e A é constante.
Se, no instante t = 0, a temperatura é de 10º C, o tempo gasto pra
que a temperatura seja mínima, em minutos, é:
a) 3, 5
b) 4, 0
c) 4, 5
d) 6, 5
e) 7, 5
Questão 07
Para um indivíduo sadio em repouso, o número N de batimentos cardíacos por minuto
varia em função da temperatura ambiente t (em graus Celsius), segundo a função
N (t ) = 0 , 1t 2 − 4t + 90 . Nessas condições, em qual temperatura o número de batimentos cardíacos por minuto é
mínimo?
a) 31º C
b) 12, 4º C
c) 20º C
d) 25º C
6
Prof. Joaquim Rodrigues
Questão 08
O físico francês Poiseuille, foi o primeiro a descobrir que o sangue flui mais perto do
centro de uma artéria do que nas extremidades.
Testes experimentais mostraram que a velocidade do sangue
num ponto a r cm do eixo central de um vaso sanguíneo é dada
pela função V ( r ) = C ( R 2 − r 2 ) em
cm/s em que C é uma constante e R é
o raio do vaso.
Supondo, para um determinado vaso,
que seja C = 1, 8 ⋅ 10 4 e R = 10 − 2 cm,
calcule:
a) a velocidade do sangue no eixo central do vaso sanguíneo;
b) a velocidade do sangue no ponto médio entre as parede do vaso e o eixo central.
Questão 09
Suponha que um grilo, ao saltar do solo, tenha sua posição no espaço descrita em função do tempo (em segundos) pela expressão h (t ) = 3t − 3t 2 , onde h é a altura máxima
atingida em metros.
a) Em que instante t o grilo retorna ao solo?
b) Qual é a altura máxima, em metros, atingida pelo grilo?
Questão 10
Uma espécie animal, cuja família no início era composta de 200 elementos, foi testada
num laboratório sob a ação de uma certa droga. Constatou-se que a lei de sobrevivência
nesta família obedecia à relação n (t ) = at 2 + b em que n(t) é igual ao número de elementos vivos no tempo t (dado em horas); a e b são parâmetros que dependem da droga
ministrada. Sabe-se que a família desapareceu (morreu seu último elemento) quando
t = 10h (após o início da experiência). Calcular quantos elementos tinha essa família 8
horas após o início da experiência.
Questão 11
Num certo dia, numa praia, a temperatura atingiu o seu valor máximo às 14 horas. Suponhamos que, nesse dia, a temperatura f(t) em graus era uma função do tempo t, medido em horas, dada por f (t ) = −t 2 + b t − 160 , quando 8 ≤ t ≤ 20 . Obtenha:
a) o valor de b;
b) a temperatura máxima atingida nesse dia;
Questão 12
De uma folha de papel retangular de 30 cm por 20 cm são retirados, de seus quatro cantos, quadrados de lado x. Determine a expressão que indica a área da parte que sobrou
em função de x.
7
Prof. Joaquim Rodrigues
Questão 13
Os diretores de um centro esportivo desejam cercar uma quadra de basquete retangular e
o espaço em volta dela com tela de alambrado. Tendo recebido 200 m de tela, os diretores desejam saber quais devem ser as dimensões do terreno a cercar com tela para que a
área seja a maior possível.
Questão 14
Deseja-se construir uma casa térrea de forma retangular. O retângulo onde a casa será
construída tem 80 m de perímetro.
Calcule as dimensões desse retângulo sabendo que a área de sua região deve ser a maior
possível.
Questão 15
Um fazendeiro precisa construir um galinheiro de forma retangular utilizando-se de uma
tela de 16 metros de comprimento. Sabendo que o fazendeiro vai usar um muro como
fundo do galinheiro, determine as dimensões do mesmo para que a sua área seja máxima.
x
x
y
Questão 16
O espaço percorrido S por um corpo em queda livre, durante um certo tempo t, é dado
pela função S (t ) = 4 , 9 t 2 .
Considerando que um corpo está em queda livre:
a) Qual é o espaço, em metros, que ele percorre após 3s?
b) Em quanto tempo ele percorre 122, 5m?
Questão 17
Uma bola é lançada ao ar. Suponha que a altura h, em metros, t segundos após o lançamento, seja h = −t 2 + 4 t + 6 .
Determine:
a) o instante em que a bola atinge a sua altura
máxima;
b) a altura máxima atingida pela bola;
c) quantos segundos depois de lançada, ela toca
o solo?
8
Prof. Joaquim Rodrigues
Questão 18
A trajetória de uma bola, num chute a gol, descreve aproximadamente uma parábola.
Supondo que a sua altura h, em metros, t segundos após o chute, seja dada pela fórmula
h = −t 2 + 6 t , determinar:
a) em que instante a bola atinge a altura máxima?
b) qual é a altura máxima atingida pela bola?
Questão 19
Nos acidentes de trânsito, uma das preocupações dos especialistas em tráfego é descobrir qual a velocidade do veículo antes da colisão.
v2
Uma das fórmulas utilizadas é d = 0,1v +
na qual v é a velocidade, em quilômetros
250
por hora, desenvolvida pelo veículo antes do choque e d, a distância, em metros, que o
mesmo percorre desde que o motorista pressente o acidente até o mesmo parar.
Essa é uma função do 2º grau que relaciona uma
distância, muitas vezes determinada pelas marcas de
pneus na pista, após utilização brusca dos freios, e a
velocidade que o carro trafegava.
Quantos metros percorre um carro a 80 km/h, desde
o momento em que vê o obstáculo, até o carro parar?
Questão 20
O impacto de colisão I (energia cinética) de um automóvel com massa m e velocidade v
é dado pela fórmula I = k m v 2 . Se a velocidade triplica, o que acontece ao impacto de
colisão de um carro de 1.000 kg?
Questão 21
Sabe-se que o custo C para produzir x unidades de certo produto é dado pela fórmula
C = x 2 − 80 x + 3.000 .
Nessas condições, calcule:
a) a quantidade de unidades produzidas para que o custo seja mínimo.
b) o valor mínimo do custo.
Questão 22
A receita diária de um estacionamento para automóveis é R = 100 p − 5 p 2 , em que p é
o preço cobrado por dia de estacionamento por carro.
a) Qual o preço que deve ser cobrado para dar uma receita diária de R$ 375,00?
b) Qual o preço que deve ser cobrado para que a receita seja máxima?
9
Prof. Joaquim Rodrigues
Questão 23
Sabe-se que o lucro total de uma empresa é dado pela fórmula L = R − C, em que L é o
lucro total, R é a receita total e C é o custo total da produção.
Numa empresa em que se produziu x unidades, verificou-se que R ( x) = 6.000 x − x 2 e
C ( x) = x 2 − 2.000 x . Nessas condições, qual deve ser a produção x para que o lucro da
empresa seja máximo?
Questão 24
A venda de x milhares de unidades de um determinado CD-ROM produzido para microcomputadores Compaq gera uma receita dada por R = 7 x − x 2 unidades monetárias.
O custo para produzir estas unidades é dado por C = x + 5 unidades monetárias (u.m).
Nestas condições:
a) determine o valor do lucro máximo (em u.m)
b) o nível de produção x para que o lucro seja máximo.
Questão 25
Define-se custo médio de produção Cm (x) o valor de produção de uma peça de um lote
de x peças. Assim, o custo médio é calculado dividindo-se o custo total pelo número de
C ( x)
. Se o custo médio de produção de certa mercadoria é
peças produzidas: Cm ( x) =
x
10
dado por Cm ( x) = − x + 3 +
e a função receita é dada por R ( x) = 10 x − 2 x 2 (x é dado
x
em milhares), obtenha o número de peças a serem produzidas para que o lucro seja máximo.
Questão 26
2.000
+ 20 + x e a
x
função receita é R ( x) = 200 x − 2 x 2 . Nestas condições, obtenha a quantidade que deve
ser produzida e vendida para maximizar o lucro.
O custo médio de fabricação de x unidades de um produto é Cm ( x) =
Questão 27
Um sitiante plantou 30 abacateiros e cada árvore produz 100 abacates em média. Pretendendo aumentar o número de árvores, o sitiante consultou um especialista que o informou que cada árvore nova plantada fará diminuir em 2 abacates o número médio
produzido pelas árvores. Nestas condições, quantas árvores ele deverá plantar para obter
o número máximo de abacates?
Questão 28
Para uma determinada viagem, foi fretado uma avião com 100 lugares. Cada pessoa deve pagar à companhia R$ 500,00 além de uma taxa de R$ 6,00 para cada lugar não ocupado do avião.
a) Qual a receita arrecadada se compareceram 80 pessoas para a viagem?
b) Qual a receita máxima que pode ser arrecadada nas condições do problema?
10
Prof. Joaquim Rodrigues
RESPOSTAS
1. a, b, f
21. a) 40
b) R$ 1.400,00
2. a) 12
b) 6
c) 2
d) 0
e) 0
22. a) 5 ou 15
b) 10
23. 2.000
24. a) 4
b) 3
3. a) −3 e 8
b) não existe raiz real
c) 3
d) −3 e 3
25. 3.500 peças
26. 30 unidades
27. 10
28. a) R$ 49.600,00
b) R$ 50.416,00
4. a) para cima
b) para baixo
c) para cima
d) para baixo
5.
6.
7.
8.
A
A
C
a) 1,8 cm/s
b) 1,35 cm/s
9. a) após 1 s
b) 0,75 m
10. 72 elementos
11. a) 28
b) 36º C
12. A( x) = −4 x 2 + 600
13. 50 x 50
14. 20 x 20
15. x = 4 e y = 8
16. a) 44,1 m
b) 5 s
17. a) 2 s
b) 10 m
c) 5,16 s
18. a) 3 s
b) 9 m
19. 33,6 m
20. O impacto será 9 vezes maior
11