hidrodinâmica - guiadafisica

HIDROSTÁTICA
HIDRODINÂMICA
Fluido
Estática versos
 A Estática os Fluidos (Hidrostática)
trata o fluido quando ele está em
repouso.
Dinâmica
A
Dinâmica
dos
Fuidos
(Hidrodinâmica) trata o fluido quando
ele está em movimento.
Fluido
 Diferentes tipos de forças atuam no sistema
F  A
 Normais
F
 Tensão 
A
Tangenciai s
Diferença fundamental entre sólidos e fluidos está na forma de
responder a tensões tangenciais.
HIDROSTÁTICA
É a parte da Hidráulica que estuda os
líquidos em repouso, bem como as forças
que podem ser aplicadas em corpos
neles submersos.
FLUIDO
É qualquer
coisa que
pode fluir,
escoar. Isto
inclui líquidos
e gases.
Densidade de um Corpo →d
m
d
VCORPO
m→massa do corpo(kg, g,...)
VC →Volume do corpo(m3, cm3, L, ...)
Massa Específica de uma Substância

m
VSUBST
.
→μ
m→massa de subst.(kg, g,...)
VS →Volume de substância(m3, cm3, L)
Essa é a
minha
aluna!
QUAL A DIFERENÇA ENTRE
DENSIDADE E MASSA ESPECÍFICA ?
A diferença entre DENSIDADE e MASSA
ESPECÍFICA fica bem clara quando falamos
de objetos OCOS. Neste caso a DENSIDADE
leva em consideração o volume completo e a
MASSA ESPECÍFICA apenas a parte que
contêm substância
*
*
d
1
x
10
kg
/
m

1
g
/
cm

1
kg
/
L
3
3
ÁGUA
3
***Para líquidos e corpos maciços não há
distinção entre densidade e massa específica.
NOS DÊ UM EXEMPLO.
Exemplo: O corpo abaixo possui massa de 2.000 g.
Determine sua densidade e a massa específica do material
que o constitui.
m
d
VCORPO
400 cm3
100 cm3
2.000
d
500
3
d4g/cm

m
VSUBST
2.000

400
5g/cm
3
RELAÇÃO ENTRE UNIDADES
As unidades mais usadas para a densidade são kg / m3 e g / cm3.
Vamos então verificar qual é a relação entre elas.
Sabemos que:
Assim:
Portanto:
1 m = 102 cm ou 1 cm = 10-2 m
1 m3 = 106 cm3 ou 1 cm3 = 10-6 m3
1 kg / m3 = 10-3 g / cm3 ou 1 g / cm3 = 103 kg/m3
Substância
Massa específica
(g/cm3)
Água
1,0
Ar
0,0013
Mercúrio
13,6
Corpo Humano
1,07
PRESSÃO
A pressão é a força a que um objeto está sujeito dividida
pela área da superfície sobre a qual a força age.
Definimos a força aqui como sendo uma força agindo
perpendicularmente à superfície.
PESO = (FORÇA)
FY
p
A
ÁREA A
N
S .I . - unid ( p)  Pa 
m²
Nkgf
; 2;atm
;cmH
2
mcm
Pressão Atmosférica
É a pressão que a atmosfera exerce sobre a
superfície da Terra. Varia de acordo com a
altitude e é possível medir o seu valor. Ao nível do
mar, ela é máxima e equivale a uma coluna de
76 cmHg (= 1 atm).
N
1atm  1,013 x10 2  76cmHg  760torr
m
5
1atm = 760mmHg
1atm = 760mmHg = 101230Pa
1atm = 760mmHg = 101230Pa = 1,0330 kgf/cm²
1atm = 760mmHg = 101230Pa =
= 1,0330 kgf/cm² = 1,01bar
1atm = 760mmHg = 101230Pa =
=1,0330 kgf/cm² = 1,01bar = 14,7psi
1atm = 760mmHg = 101230Pa =
=1,0330 kgf/cm² = 1,01bar = 14,7psi = 10,33mca
Converta as unidades de pressão para o
sistema indicado. (utilize os fatores de
conversão apresentados na tabela).
a) converter 2atm em Pa.
b) converter 3000mmHg em psi.
c) converter 30psi em bar.
d) converter 5mca em kgf/cm².
e) converter 8bar em Pa.
f) converter 10psi em Pa.
Altitude (m)
Altitude (m)
Pressão
(mmHg)
0
Pressão
atmosférica
(mmHg)
760
1200
658
200
742
1400
642
400
724
1600
627
600
707
1800
612
800
690
2000
598
1000
674
3000
527
Experiência de Torricelli
Torricelli,
físico
italiano,
realizou
uma
famosa
experiência que, além de
demonstrar que a pressão
existe realmente, permitiu a
determinação de seu valor.
Torricelli encheu de mercúrio
(Hg) um tubo de vidro com mais
ou
menos
1
metro
de
comprimento;
em
seguida
fechou a extremidade livre do
tubo e o emborcou numa
vasilha contendo mercúrio.
Quando a extremidade do
tudo foi aberta, a coluna de
mercúrio desceu, ficando o seu
nível aproximadamente 76 cm
acima do nível do mercúrio
dentro da vasilha.
p x = py
Mas px = patm e py = pcoluna,
assim: patm = pcoluna
Pressão Hidrostática
É a pressão exercida por um líquidoUma coluna de
líquido de densidade  exerce pressão e que essa
pressão vale p =  · g · h, sendo h a profundidade ou
a altura da coluna..
pH .g.h
SI→ N/m2 kg/m3 m/s2 m
P
A
h
h p 
Variação da pressão exercida por um líquido
Pode-se demonstrar, de uma forma
muito simples, a variação de pressão
com a altura. Basta, para isso,
fazermos perfurações num recipiente
cheio de líquido em posições
diferentes. O jorro sairá cada vez mais
forte à medida que aumentarmos a
altura da coluna de líquido (isto é, nos
pontos mais baixos).
Para dois líquidos temos:
pH = μ1.g.h1 + μ2.g.h2
VALOR DA PRESSÃO ATMOSFÉRICA
Pascal repetiu a experiência no alto de uma montanha e
verificou que o valor da pressão atmosférica era menor do
que ao nível do mar. Concluiu que quanto maior for a altitude
do local, mais rarefeito será o ar e menor será a altura da
camada de ar que atuando na superfície de mercúrio.
VARIAÇÃO DA PRESSÃO ATMOSFÉRICA COM A ALTITUDE
ALTITUDE (m)
PRESSÃO ATMOSFÉRICA (cm Hg)
0
500
1.000
2.000
3.000
76 (10,33 mH2O) (MCA)
72
67
60
53 (7,21 mH2O) (MCA)
PRESSÃO TOTAL OU ABSOLUTA
A pressão no interior de um líquido em equilíbrio
é a soma da pressão atmosférica e da pressão
da coluna de líquido.
Patm
1
h
2
p = patm +  · g · h
(PRESSÃO ABSOLUTA)
PRESSÕES ABSOLUTAS
p
PRESSÕES RELATIVAS
p= ·g·h
p = patm +  · g · h
p
.g.h
.g.h
pat
pat
m
m
1 atm = 10,33 mH2O
0
(Vácuo absoluto)
-10,33
mH2O
PRESSÕES
POSITIVAS
0
PRESSÕES
NEGATIVAS
(Vácuo absoluto)
Teorema de Stevin
Os pontos 1 e 2 estão no interior de um fluido de densidade
d.
pA =  . g . hA
pB =  . g . hB
Fazendo pB – pA, temos:
pB – pA = . g . hB –  . g . hA
pB – pA =  . g (hB – hA)
pB – pA =  . g . h
pA = pB + . g . h
Δp = μ.g.Δh
PARADOXO HIDROSTÁTICO
Num fluido qualquer, a pressão não é a mesma em todos os pontos.
Porém, se um fluido homogêneo estiver em repouso, então todos os
pontos numa superfície plana horizontal estarão à mesma pressão.
A pressão nas linhas marcadas na figura será a mesma,
se estiverem em um mesmo plano horizontal
UHMM?
NÃO ESTAMOS NA
MESMA ALTURA, HÁ
ALGO ERRADO!
AH, BOM!
p0    g  h
Se colocarmos dois líquidos não
Quando líquidos não
miscíveis num tubo em forma de miscíveis são colocados em
um recipiente, eles se
U, as alturas alcançadas pelos
dispõem do fundo para a
líquidos, contadas a partir da
superfície de separação, são boca do recipiente, segundo
inversamente proporcionais as a ordem decrescente das
suas densidades: a
massas específicas dos
superfície de separação
líquidos.
entre dois líquidos não
miscíveis é plana e
horizontal.
H1  2

H 2 1
Teorema de Pascal
A pressão aplicada a um fluido dentro de um recipiente
fechado é transmitida, sem variação, a todas as partes do
fluido, bem como às paredes do recipiente.
Aplicação:
Prensa Hidráulica
F1 F2

A1 A2
Os Fluidos e pressão hidrostática
Princípio de Pascal
F0 Fi

A0 Ai
, donde
A0
F0  Fi
Ai
Quando o piston da esquerda desce o da
direita sobe (o fluido conserva-se e é
incompressível
Volume  Ai  d i  Ao  d 0
, donde
Ai
d0  di 
A0
 A0  
Ai 



W  F0  d 0   Fi    d i    Fi  d i
 Ai   A0 
“O trabalho realizado sobre o sistema em i, é igual ao cedido
pelo sistema em o”
Na prensa hidráulica no
êmbolo menor uma dada
força e deslocamento,
induzem no maior uma
maior força e menor
deslocamento...
Princípio de Arquimedes
Todo corpo imerso total ou parcialmente num líquido recebe
uma força vertical, de baixo para cima, igual ao peso da
porção de líquido deslocada pelo corpo.
Empuxo
Força vertical de baixo para cima que o líquido exerce
sobre o corpo imerso. É o peso do liquido deslocado.
E = md .g
md
Como,  l 
md = l .Vd,
Vd
substituímos: E = l . Vd . g
A causa do empuxo é o fato de a pressão aumentar com a
profundidade!
HIDRODINÂMICA
A Hidrodinâmica é a parte da Física que estuda as propriedades
dos fluidos em movimento .
O nosso estudo da Hidrodinâmica determina algumas condições
iniciais: o fluido tratado aqui será sempre ideal, ou seja, nãoviscoso, homogêneo e velocidade de escoamento constante em
um determinado ponto em relação ao tempo (regime
estacionário).
O movimento de fluidos ideais
Os fluidos ideais são:
... de fluxo estacionário (laminar) - em cada ponto a velocidade
(vetorial) do fluido não muda com o tempo.
... Incompressíveis - a densidade é homogênea e constante
= const.
... de escoamento não viscoso - a velocidade na interface de
contacto com o contentor é a mesma que no interior do fluido.
... irrotacionais - cada elemento de volume não roda em torno dum
seu eixo central.
Escoamento rotacional ou turbulento. O escoamento
turbulento é um escoamento irregular, caracterizado por regiões
de pequenos vórtices. Como exemplo, o escoamento da água
numa corrente fica turbulento nas regiões onde as rochas, ou
outros obstáculos, estão no leito e contribuem para a formação
dos rápidos encachoeirados
O Escoamento se diz laminar ou estacionário se cada partícula do fluido
segue uma trajetória definida e suave, e se as trajetórias das partículas não
se cruzam.
No escoamento laminar, portanto, a velocidade do fluido, em cada ponto,
permanece constante com o tempo. Ex.: a água se movendo num rio calmo ,
de leito regular e sem obstáculos.
ESCOAMENTO ESTÁCIONÁRIO
Equação da continuidade
A1v1 = A2v2
EQUAÇÃO DE BERNOULLI
2
2
dv
dv
1
2
P

dgh


P

dgh

1
1
2
2
2
2
Equação de Bernoulli
EQUAÇÃO DE BERNOULLI
1 2
p   v   gy  constante
2
Equação de Bernoulli afirma que o trabalho realizado pelo fluido
das vizinhanças sobre uma unidade de volume de fluido é igual a
soma da energia cinética e potencial ocorridas na unidade de
volume durante o escoamento.
 Ou a equação de Bernoulli é a soma das pressões devido a
diferença de velocidade e altura.
Equação de Bernoulli
 Relação entre pressão, velocidade e altura no escoamento
– Equação de Bernoulli.
 Aplicações:
 escoamento em sistemas de
escoamento;
 voos de aeronaves;
 usinas hidroelétricas.
SUSTENTAÇÃO DE AVIÕES
As asas são construídas de forma a que o ar se mova mais depressa na parte
de cima da asa, fazendo com que a pressão por cima da asa seja mais baixa
Aplicações da equação de Bernoulli
• Teorema de Torricelli
v  2gh
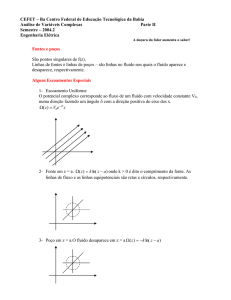
Tubo de Venturi
• O Tubo de Venturi é um elemento medidor de
vazão de diferencial de pressão, também
chamado de medidor de vazão por obstrução de
área. A diferença de pressão entre duas seções
distintas do medidor é proporcional à vazão que
escoa por ele.
• Algumas das principais razões de usar
elementos de obstrução para se medir vazão
são as seguintes:
• Podem ser usados para medir qualquer fluido.
• Não há nenhum elemento mecânico imerso no
escoamento.
• Não há limite de vazão a ser medida, ou seja, a
tubulação pode ter qualquer diâmetro
Tubo de Venturi
Tubo de Venturi
v1 
2 gh
 A1 

 A 

 2 
2
1
Tubo de Pitot
2d M  d .gh
v
d
Tubo de Pitot
- O Tubo de Pitot no avião serve
para 2 Finalidades
- Marcar a velocidade relativa (
Ve ocimetro ) entre a aeronave e o
ar ( Chamado de Air Speed )
- Marcar a Altitude ou a Altura (
Altimetro ) com a qual a aeronave
está sobrevoando .
Em um carro de F1 o tubo de Pitot
controla a pressão do ar, e pode
diminuir, no caso de estar
erradamente colocado, em cerca
de 7 cavalos a potencia do motor
FIM DA AULA