PROF. CLAUDIO AUGUSTO TURMA: 7o SEMESTRE/2011

CURSO: SISTEMA DE INFORMAÇÃO
DISCIPLINA: MATEMÁTICA DISCRETA
PROF. CLAUDIO AUGUSTO
TURMA: 7o SEMESTRE/2011
EXERCÍCIOS PROPOSTOS (L2 – UNIDADE 01 - GABARITO)
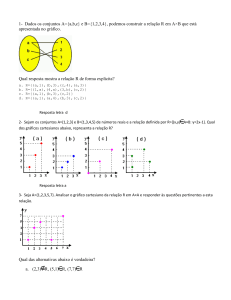
(01) Classificar as funções abaixo, em injetora, sobrejetora ou bijetora (justificando cada resposta).
(a) Injetora, pois elementos distintos do conjunto A estão em correspondência com elementos distintos do
conjunto B.
(b) Bijetora, pois para elementos distintos do conjunto A correspondem elementos distintos do conjunto B e
Im(f) = B.
(c) Sobrejetora, pois o conjunto imagem da função é o próprio conjunto B.
(d) Não é injetora, pois pelo menos um elemento de B é imagem de mais de um elemento de A.
Não é sobrejetora, pois o conjunto imagem da função não é o próprio conjunto B.
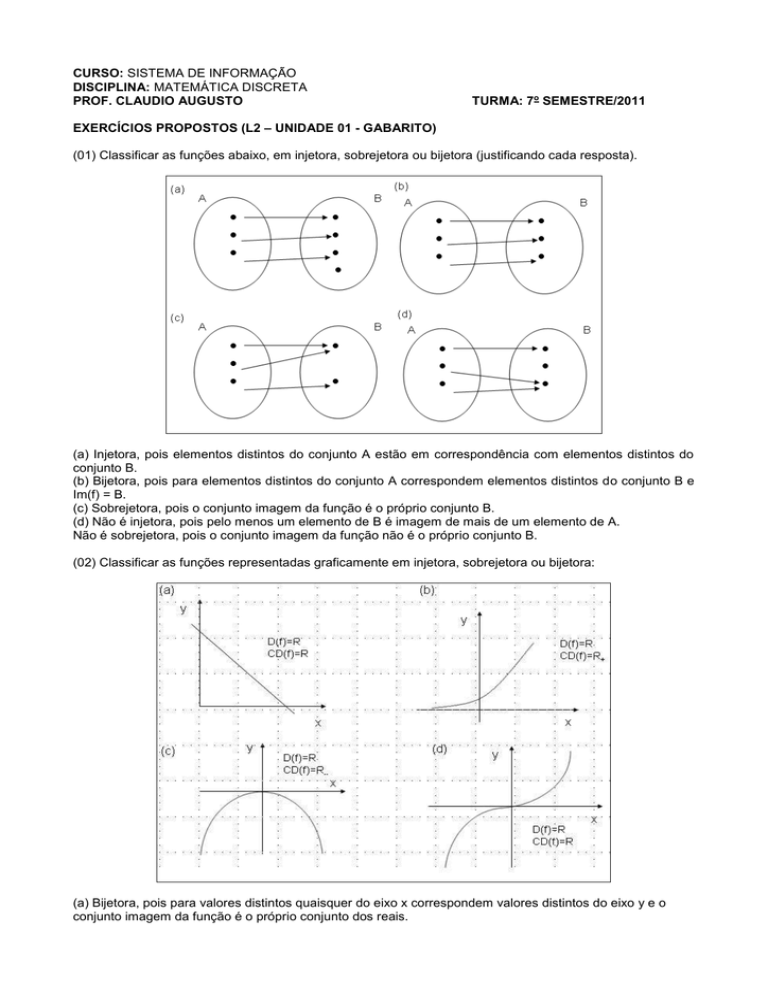
(02) Classificar as funções representadas graficamente em injetora, sobrejetora ou bijetora:
(a) Bijetora, pois para valores distintos quaisquer do eixo x correspondem valores distintos do eixo y e o
conjunto imagem da função é o próprio conjunto dos reais.
(b) Injetora, pois para valores distintos quaisquer do eixo x correspondem valores distintos do eixo y.
(c) A função é sobrejetora, pois Im(f) = CD(f).
Não é injetora, pois pelo menos um elemento (y) do CD(f) é imagem de dois elementos distintos do D(f).
(d) (a) Bijetora, pois para valores distintos quaisquer do eixo x correspondem valores distintos do eixo y e o
conjunto imagem da função é o próprio conjunto dos reais.
(03) Determinar a lei da função inversa de cada função dada por:
(a) y  2 x  4
x2
x 1
(c) y  x  5
(b) y 
(d) y  x  4
x1
(e) y  3 x
(f) y  2 x  1
(a)
(b)
(c)
(d)
(e)
(f)
(04) Dada a função f por f(x)=3x -2, calcular f-1(4).
(05) Determinar f-1(2) + f--1(-2), sabendo que f(x) = 3x +1.
(06) Esboce o gráfico e identifique como crescente ou decrescente as funções exponenciais:
(a) f ( x ) 
x
3
1
(b) f ( x )   
 3
(c) f ( x ) 
5
(d) f ( x) 
2
x
x
x
(07) Numa determinada cultura há bactérias em condições ideais. A cada duas horas a quantidade dobra.
Determinar o número de bactérias, 12 horas após o início do estudo.
bactérias.
N(t) = número de bactérias no tempo t.
No = número de bactérias no tempo t = 0
No = 200
(8) Curva de aprendizagem é um conceito criado por psicólogos que constataram a relação existente entre a
eficiência de um individuo e a quantidade de treinamento ou experiência possuída por esse indivíduo. Um
exemplo de Curva de Aprendizagem é dado pela expressão Q  700  400.
0 , 5t
e
, onde Q = quantidade
de peças produzidas mensalmente por um funcionário; t = meses de experiência e e  2,718.
(a) De acordo com essa expressão, quantas peças um funcionário com dois meses de experiência deverá
produzir mensalmente?
(b) E um funcionário, sem qualquer experiência, quantas peças deverá produzir mensalmente?
(09) Uma fórmula matemática para se calcular aproximadamente a área, em metros quadrados, da
superfície corporal de uma pessoa, é dada por: S ( p ) 
11
100
p
2/3
, onde p é a massa da pessoa em
quilogramas. Considere uma criança de 8 Kg. Determine:
(a) a área da superfície corporal da criança.
(b) a massa que a criança terá quando a área de sua superfície corporal duplicar. (Use aproximação
2  1,4 .
(10) Dê o domínio e o conjunto imagem das funções e em seguida construa o esboço do gráfico cartesiano
das mesmas.
 1 

 1000 
x
(a) f(x) = 
D(f) = R
Im(f) =
(b) f(x) = log1/10000 x
D(f) =
Im(f) = R
(c) f(x) = log200 (x – 1)
D(f) =
Im(f) = R
(11) Dentre As funções exponenciais seguintes, identifique as que são crescentes e as que são
decrescentes:
(a)
(b)
(c)
(e)
(f)g
(12) Suponha que o número de indivíduos de uma população seja dado pela função:
a variável t é dada em anos e a e b são constantes.
em que
(a) Encontre as constantes a e b de modo que a população inicial (t=0) seja igual a 1024 individuos e a
população após 10 anos seja a metade da população inicial.
t = 0 anos
1024 indivíduos
t = 10 anos
1024 x 1/2 = 512 indivíduos
(b) Qual o tempo mínimo para que a população se reduza a 1/8 da população inicial?
t=?
1024 x 1/8 = 128 indivíduos