geometria gráfica

GEOMETRIA GRÁFICA
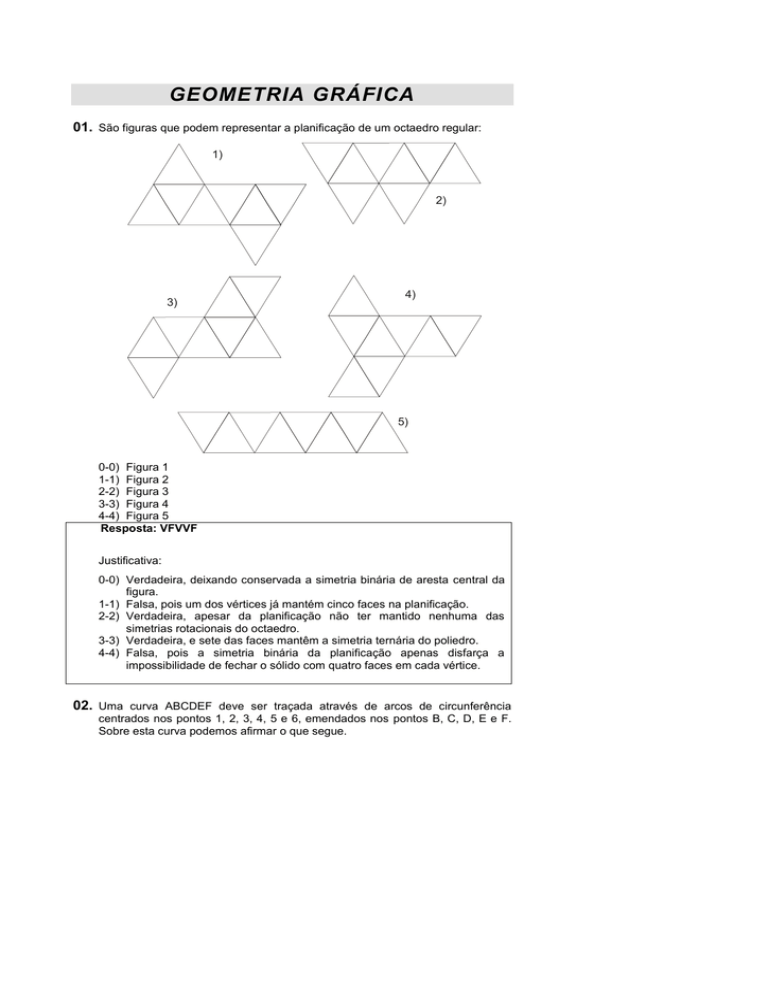
01. São figuras que podem representar a planificação de um octaedro regular:
1)
2)
3)
4)
5)
0-0) Figura 1
1-1) Figura 2
2-2) Figura 3
3-3) Figura 4
4-4) Figura 5
Resposta: VFVVF
Justificativa:
0-0) Verdadeira, deixando conservada a simetria binária de aresta central da
figura.
1-1) Falsa, pois um dos vértices já mantém cinco faces na planificação.
2-2) Verdadeira, apesar da planificação não ter mantido nenhuma das
simetrias rotacionais do octaedro.
3-3) Verdadeira, e sete das faces mantêm a simetria ternária do poliedro.
4-4) Falsa, pois a simetria binária da planificação apenas disfarça a
impossibilidade de fechar o sólido com quatro faces em cada vértice.
02. Uma curva ABCDEF deve ser traçada através de arcos de circunferência
centrados nos pontos 1, 2, 3, 4, 5 e 6, emendados nos pontos B, C, D, E e F.
Sobre esta curva podemos afirmar o que segue.
0-0) Há concordância entre os arcos no ponto B.
1-1) Há concordância entre os arcos no ponto C.
2-2) Há concordância entre os arcos no ponto D.
3-3) Há concordância entre os arcos no ponto E.
4-4) Há concordância entre os arcos no ponto F.
Resposta: VVFFV
Justificativa:
O princípio básico entre arcos de circunferência permite que o candidato
verifique cada ponto de passagem de um arco para o seguinte apenas
testando com a régua o alinhamento entre esse ponto e os centros dos arcos
que nele concorrem. Se ignorar tal princípio, precisará traçar a compasso toda
a curva e dependerá de muita sensibilidade visual para perceber a quebra da
curva nos pontos em que não há concordância.
0-0) Verdadeira, pelo alinhamento de B com os centros 1 e 2.
1-1) Verdadeira, pelo alinhamento de C com os centros 2 e 3.
2-2) Falsa, pelo desalinhamento de D com os centros 3 e 4.
3-3) Falsa, pelo desalinhamento de E com os centros 4 e 5.
4-4) Verdadeira, pelo alinhamento de F com os centros 5 e 6.
03. Um triângulo (ABC) tem as seguintes medidas: lado (AB)=6cm, ângulo em
(C)=60o,e altura de (A)=3cm. Sobre esse triângulo, podemos afirmar que:
0-0) seu ortocentro está no seu interior.
1-1) seu circuncentro está no seu exterior.
2-2) seu perímetro mede mais de 15cm.
3-3) sua área mede menos de 11cm2.
4-4) o raio do círculo inscrito mede menos de 2cm 1,5cm.
Resposta: FFVVV
Justificativa:
Haverá toda a vantagem na resolução gráfica, usando os instrumentos de
desenho. Partindo de um segmento com a medida do lado AB, traça-se sobre
ele o arco capaz de ângulo oposto. Um arco de circunferência centrado em A,
com o raio medindo a altura dada, permite o traçado do lado BC tangente a tal
arco, indo localizar o vértice C no arco capaz.
Pelo valor do ângulo dado, não é difícil a resolução da questão através da
trigonometria.
0-0) Falsa, pois o triângulo é acutângulo.
1-1) Falsa, pois o triângulo é acutângulo.
2-2) Verdadeira, pois o perímetro mede 16,8 cm2.
3-3) Verdadeira, pois a área mede 12 cm2.
4-4) Verdadeira, pois o raio do círculo inscrito mede 1,4 cm.
O triângulo ABC é retângulo. O seno do ângulo do triângulo com vértice em B
é ½ e, portanto, este ângulo mede 30 o (não poderia ser 150o, uma vez que o
triângulo já tem um ângulo interno medindo 60 o). Segue que o ângulo do
triângulo com vértice em A mede 180o-60o-30o = 90o, e ABC é um triângulo
retângulo. Temos AC = 3/sen 60o = 2 3 cm e BC = 12  36  4 3 cm.
O ortocentro do triângulo coincide com o vértice A, logo não está no interior
do triângulo, e 0-0 é falsa.
O circuncentro do triângulo é o ponto médio da hipotenusa BC, logo não está
no exterior do triângulo, e 1-1 é falsa.
O perímetro do triângulo mede 6 + 2 3 + 4 3 = 6(1+ 3 ) ≈ 16,392cm que é
maior que 15, e 2-2 é verdadeira. Observe que o valor exato do perímetro,
16,392..., é diferente do valor obtido graficamente em pelo menos 0,41cm, um
erro de pelo menos 2,5%.
A área do triângulo mede 4 3 .3/2 = 6 3 cm2 ≈ 10,392cm2, portanto 3-3 é
verdadeira.
O raio do círculo inscrito mede 6 3 /[3(1+ 3 )] = (3 4 é verdadeira.
3 ) cm ≈ 1,268cm e 4-
04. Seccionando um hexaedro regular por planos paralelos ao plano (ABC),
podemos obter um:
B
A
C
0-0) Triângulo eqüilátero.
1-1) Quadrado.
2-2) Retângulo.
3-3) Hexágono regular.
4-4) Losango.
Resposta: VFFVF
Justificativa:
Percebendo que o plano ABC corta perpendicularmente a diagonal do cubo,
que é um eixo de simetria ternária, o candidato concluirá que a figura
resultante de cortes paralelos a ABC só poderá ser polígono de número de
lados múltiplo de três.
0-0) Verdadeira, pois a própria seção (ABC) é eqüilátera.
1-1) Falsa, uma vez que (ABC) não é paralela às faces do cubo.
2-2) Falsa, pois (ABC) precisaria ser paralelo a uma aresta.
3-3) Verdadeira, desde que o plano de seção passe pelo ponto médio de seis
arestas.
4-4) Falsa, pois o losango é polígono de quatro lados.
05. A maior parte das letras maiúsculas do alfabeto latino, em seu desenho mais
simples, são figuras simétricas. Sobre este tema é possível afirmar que:
0-0) Apenas as letras H, I, O e X têm centro de simetria.
1-1) Mais da metade tem eixo de simetria.
2-2) As letras H, I, O e X têm dois eixos de simetria.
3-3) Algumas letras têm centro de simetria sem ter eixo de simetria.
4-4) As letras J, G e F não têm eixo de simetria.
Resposta: FVVVV
Justificativa:
Questão de identificação de centro e eixos de simetria, usando formas bem
visualizadas por todos os candidatos.
0-0) Falsa, pois o centro de simetria não depende do cruzamento de eixos de
simetria ortogonais.
1-1) Verdadeira, incluindo as letras que só têm um eixo e as que têm dois
eixos de simetria.
2-2) Verdadeira, pois as letras H, I, O, e X têm um eixo horizontal e outro
vertical.
3-3) Verdadeira, pois as letras N, S e Z têm centro de simetria, mas nenhum
eixo.
4-4) Verdadeira, pois J, G e F não têm nem eixo horizontal nem vertical.
06. A poltrona representada esquematicamente em isometria na primeira figura
pode ser representada em escala reduzida e outras posições nas demais
figuras.
0-0) Pode aparecer como na figura 1.
1-1) Pode aparecer como na figura 2.
2-2) Pode aparecer como na figura 3.
3-3) Pode aparecer como na figura 4.
4-4) Pode aparecer como na figura 5.
Resposta: VFFVF
Justificativa:
Não há necessidade de nenhum traçado. O candidato poderá precisar
confirmar as medidas de cada figura para verificar a proporcionalidade das
arestas, garantida na isometria, mesmo quando a escala é reduzida. O mais
importante para o acerto da resposta é a capacidade viso-motriz do
candidato.
0-0) Verdadeira, pois representa a poltrona emborcada.
1-1) Falsa, pois a figura 2 representa uma poltrona simétrica, tombada de
costas.
2-2) Falsa, pois a figura 3 representa uma poltrona simétrica tombada de lado
e vista por baixo.
3-3) Verdadeira, pois representa a mesma poltrona, vista pelo lado direito.
4-4) Falsa, pois a figura 5 representa uma poltrona simétrica, tombada de
lado e vista por trás.
07. Sobre qualquer pentágono regular estrelado, podemos afirmar:
A
B
C
F
D
E
0-0) O ângulo no vértice A mede 36o.
1-1) Existe centro de simetria.
2-2) São cinco os eixos de simetria.
3-3) ( AB )/( BC )=( AC )/( AB ).
4-4) A área do núcleo (BCDEF) mede 1/3 da área total do estrelado.
Resposta: VFVVF
Justificativa:
Os conhecimentos de geometria plana obtidos pelo candidato na matemática
do ensino fundamental e do ensino médio dificilmente chegam ao nível desta
questão, mas a obtenção das medidas sobre a figura, executada com toda a
precisão, permite que ele obtenha as respostas certas.
0-0) Verdadeira, pois o ângulo em A está inscrito na circunferência
circunscrita ao pentágono, determinando nesta um arco de 72º.
1-1) Falsa, pois não há equinversão que transforme cada ponto da figura em
um ponto simétrico na mesma figura.
2-2) Verdadeira, pois AD e as quatro outras retas que partem das outras
pontas para os vértices B, C, E e F dividem a estrela em duas metades
simétricas.
3-3) Verdadeira, pois AB é o segmento áureo de AC.
4-4) Falsa, pois o apótema do pentágono BCDEF é menor que a metade da
altura de cada triângulo isósceles que constitui uma ponta da estrela.
Assim, a soma das áreas dos cinco triângulos que o centro do polígono
determina com os lados BC, CD, DE, EF e FB é menor que a metade da
soma das áreas das cinco pontas. Todo o núcleo BCDEF terá então área
inferior a 1/3 da área total do pentágono estrelado.
08. Dado um quadrilátero convexo (ABCD) qualquer, localize os pontos I, J, K e L,
médios respectivos de AB, BC, CD e DA. Sobre este quadrilátero, podemos
afirmar que:
0-0)
1-1)
2-2)
3-3)
4-4)
a área de (IJKL) é metade da área de (ABCD).
(IJKL) é um quadrado se e somente se (ABCD) é um quadrado.
(IJKL) é um paralelogramo para qualquer quadrilátero (ABCD).
(IJKL) e (ABCD) são semelhantes.
(IJKL) é um retângulo se e somente se as diagonais de (ABCD) são
perpendiculares.
Resposta: VFVFV
Justificativa:
Traçando as diagonais do quadrilátero inicial, podemos observar, pela
propriedade de Tales, que, no triângulo (ABD), o segmento (IL) é paralelo a
(BD) e mede metade do seu comprimento. No triângulo (CBD), o segmento
(JK) também é paralelo (BD) e mede metade do seu comprimento. Logo,
podemos deduzir que (IL) e (JK) são paralelos e de mesmo comprimento; ou
seja, (IJKL) é um paralelogramo. O mesmo raciocínio mostra que (IJ) e (LK)
são paralelos a (AC) e medem metade do seu comprimento.
0-0) Verdadeira: Considerando os pontos (M) e (N) de interseção dos lados
(IJ) e (LK) do paralelogramo (IJKL) com (BD), (MNKJ) e (MNLI) são
paralelogramos. A área de (MNKJ) é a metade da área de (BCD), uma
1-1)
2-2)
3-3)
4-4)
vez que a altura e a base de (MNKJ) correspondem á metade da altura e
da base do triângulo (BCD). Do mesmo modo, a área de (MNLI) é a
metade da área de (ABD). Logo, a área de (IJKL) é a metade da área de
(ABCD).
Falsa: Qualquer que seja o quadrilátero (ABCD), (IJKL) é um
paralelogramo de lados paralelos às diagonais de (ABCD) e de
comprimentos medindo a metade das respectivas diagonais. Para que
(IJKL) seja um quadrado, o quadrilátero (ABCD) deve ter suas diagonais
de mesmo comprimento e perpendiculares entre si; no entanto, existem
quadriláteros que têm diagonais perpendiculares e de mesmo
comprimento, e que não são quadrados.
Verdadeira: Ver justificativa.
Falsa: Já que (IJKL) é um paralelogramo para qualquer quadrilátero
(ABCD), não existe sempre semelhança entre (ABCD) e (IJKL).
Verdadeira: O paralelogramo (IJKL) tem seus lados paralelos às
diagonais de (ABCD). (IJKL) é um retângulo quando seus lados
consecutivos são perpendiculares; ou seja, quando as diagonais de
(ABCD) são perpendiculares entre si.
09. Considerando quatro pontos fixos A, B, C e D e um ponto móvel M e
construindo o ponto M1 simétrico de M em relação com A; o ponto M2 simétrico
de M1 em relação a B; o ponto M3 simétrico de M2 em relação a C; e o ponto M4
simétrico de M3 em relação com D, podemos afirmar que:
0-0) o segmento MM4 varia em comprimento, direção e orientação,
dependendo da posição do ponto M.
1-1) M e M4 são confundidos para qualquer posição de M quando os pontos
ABCD formam um paralelogramo.
2-2) M e M4 são confundidos somente quando M fica na interseção das
diagonais do quadrilátero ABCD.
3-3) para qualquer posição de M, o segmento MM4 é constante em
comprimento, orientação e direção.
4-4) o comprimento de MM4 é constante e igual à diferença entre os
comprimentos de AB e CD.
Resposta: FVFVF
Justificativa:
Temos diversas possibilidades para resolver essa questão:
a) Geometricamente: Podemos observar no triângulo (MM1M2) que (A) e (B) são
pontos médios respectivos de (MM1) e (M1M2), pela propriedade de simetria,
e que, no triângulo (M2M3M4), (C) e (D) são pontos médios respectivos de
(M2M3) e (M3M4); logo, (MM2) é paralelo, mede o dobro de sua medita e tem
mesmo sentido que (AB); (M2M4) é paralelo, mede o dobro de sua medida e
tem o mesmo sentido que (CD). (A), (B), (C) e (D) são pontos fixos; logo,
(MM2) e (M2M3) são fixos em direção e comprimento e, por sua vez, (MM4) é
fixo em comprimento e direção.
b) Por vetores: Temos (MM4) = (MM1) + (M1M2) + (M2M3) + (M3M4) = 2(AM1)
+2(M1B) +2(CM3) +2(M3D) = (AB) + (CD).
c) Pelas transformações: O ponto (M4) é a imagem de (M) depois de 4 simetrias
centrais; ou seja, depois de 4 rotações de 180º. O produto dessas
transformações é uma translação, ou seja, (MM4) é constante em direção,
comprimento e sentido.
M1
B
M2
A
C
M3
M
D
M4
0-0) Falsa: Ver justificativa: (MM4) é constante em comprimento, direção e
sentido.
1-1) Verdadeira: Segundo a justificativa, (MM2) é paralelo e mede o dobro de
(AB), e (M2M4) é paralelo e mede o dobro de (CD). Se (ABCD) forma um
paralelogramo, (MM2) e (M2M4) são de mesmo comprimento, paralelos e de
sentido oposto; logo (M) e (M4) são coincidentes.
2-2) Falsa: (MM4) sendo constante em comprimento, direção e sentido para (A),
(B), (C) e (D) dados. O fato de (M) e (M4) coincidirem não depende da
posição do ponto (M). De fato, (M) e (M4) são coincidentes somente quando
(ABCD) é um paralelogramo.
3-3) Verdadeira: Ver justificativa.
4-4) Falsa: Isso somente acontece quando (M) e (M4) são coincidentes.
10. Um terreno tem o formato do quadrilátero ABCD, representado na escala 1/500.
Dessa forma, podemos afirmar que:
B
A
D
C
0-0) existe um ponto eqüidistante dos quatro vértices.
1-1) é possível construir um prédio cilíndrico tangente aos quatro lados do
terreno.
2-2) a área do terreno mede mais de 300m2.
3-3) o perímetro do quadrilátero é menor que 90m.
4-4) o quadrilátero cujos vértices são os pontos médios dos lados de (ABCD) é
um paralelogramo cuja área mede a metade da área do terreno.
Resposta: VFFVV
Justificativa:
A percepção de dois ângulos retos opostos identifica o quadrilátero dado
como inscritível no círculo.
Se tais ângulos não forem identificados pelo candidato, ele poderá responder
corretamente a questão, mas terá um pouco mais de trabalho.
0-0) Verdadeira, pois o centro da circunferência circunscrita ao quadrilátero
será o ponto eqüidistante dos quatro vértices.
1-1) Falsa, pois o quadrilátero dado não é circunscritível ao círculo, o que
pode ser constatado pela desigualdade das somas das medidas de lados
opostos. Sem conhecer tal propriedade, o candidato terá que traçar uma
circunferência tangente a três lados do quadrilátero e verificar que ela
não tangencia o quarto lado.
2-2) Falsa, pois a divisão do terreno em dois triângulos retângulos facilita o
cálculo de suas áreas, de 125m2 e 147 m2, levando a uma área total bem
menor que 400m2
3-3) Verdadeira, pois a simples conversão de escala determina o perímetro
do terreno, medindo 71m.
4-4) Verdadeira, pois tal propriedade é geral para os quadriláteros, e pode ser
demonstrada fácilmente através do teorema de Tales. Se desconhecida
pelo candidato, ele ainda poderá constatá-la graficamente, apesar de
perder bastante tempo no cálculo das áreas.
11. A figura abaixo é o perfil de uma chapa metálica em forma de meia coroa
circular, que pode ser dobrada e soldada para a construção de um funil em
forma de tronco de cone. A respeito da chapa e do funil, podemos afirmar que:
0-0)
1-1)
2-2)
3-3)
4-4)
o raio da boca do funil mede a metade do raio externo da coroa circular.
a área da chapa é inferior a 25cm².
o volume do funil é maior que 15ml.
a altura do tronco de cone é 75% da altura total do cone que o gerou.
a geratirz do tronco de cone é inferior a 3,5cm
Resposta: VVFVV
Justificativa:
0-0) Verdadeira, pois o perímetro da base do cone mede a metade da
circunferência externa da coroa inteira, sendo 0,5 a razão entre os raios.
1-1) Verdadeira, pois a área da meia coroa, calculada com os raios de 4 cm e
1 cm, fica em torno de 23,55 cm².
2-2) Falsa, já que o volume do funil mede em torno de 14,23ml.
3-3) Verdadeira, pois as alturas são proporcionais aos raios, medidos como 4
cm e 1 cm.
4-4) Verdadeira, pois a medida da geratiriz do troco de cone, obtida na figura,
é de 3cm.
12. Um cubo representado em linha tracejada na cavaleira da figura, com aresta
medindo 4 cm, foi transformado no sólido composto de parte poliédrica e parte
cônica. A respeito deste sólido, podemos afirmar o que segue.
0-0) A parte poliédrica tem volume menor que 31cm³.
1-1) A porção eliminada da metade posterior do cubo pelo plano que secionou
seu vértice superior direito tem volume que não chega a 1cm³.
2-2) A representação do sólido não permite garantir que a parte cônica seja a
quarta parte de um cone de revolução.
3-3) A área da face mistilínea do sólido prismático na metade posterior do cubo
mede menos de 10 cm²
4-4) O volume total do sólido composto é inferior a 33,5 cm³.
Resposta: VFVFV
Justificativa:
0-0) Verdadeira, pois o volume total do prisma, antes de ser cortado no canto
superior direito, mede 32 cm³, e mesmo que nada seja cortado na parte
posterior, não mostrada na perspectiva, o corte mostrado na figura já
reduz mais de 1 cm³ no seu volume.
1-1) Falsa, já que o volume da pirâmide subtraída ao prisma mede 1,3 cm³.
2-2) Verdadeira, pois a cavaleira da figura não está mostrando as faces
lateral e inferior da parte cônica, e estas podem não pertencer às faces
do cubo original.
3-3) Falsa, pois esta face está em verdadeira grandeza na cavaleira e,
subtraindo do quadrado um triângulo e um quarto de círculo, a área
obtida fica com 10,86 cm².
4-4) Verdadeira, pois, com as medidas tomadas na figura, o volume total do
sólido fica em torno de 32,8 cm³.
13. Uma caixa d´água, em forma de tronco de pirâmide octogonal, está
representada na figura em vistas ortogonais, na escala de 1/100, onde se
despreza a espessura de suas paredes. Sobre essa caixa d´água, podemos
afirmar: Falta uma vista.
0-0) A altura da pirâmide que gerou o tronco mede 3m.
1-1) A área da base inferior é 1/3 da área da base superior.
2-2) A aresta lateral mede mais que 2,3m.
3-3) A área lateral total do tronco de cone mede mais que 20m².
4-4) O volume total da caixa d’água mede mais que 9,5 m³.
Resposta: VFVFV
Justificativa:
0-0) Verdadeira, pois, prolongando as arestas laterais na vista de frente ou
medido a altura do tronco e usando as propriedades da homotetia, o
candidato concluirá pela veracidade da proposição.
1-1) Falsa, desde que a razão entre as médidas lineares das duas bases é
que vale 1/3, o que acarreta 1/9 como a razão entre as áreas.
2-2) Verdadeira, pois a altura das faces está em verdadeira grandeza no
contorno da vista de frente, e mede 2,3 cm. Então, a aresta da caixa
d’água será necessariamente maior que 2,3m.
3-3) Falsa, pois, a partir da medida 2,3m para a altura das faces laterais, que
são trapézios de base medindo 1,5m e 0,5m, a área lateral das oito faces
fica com 18,4 m².
4-4) Verdadeira, pois, calculando as áreas das bases octogonais e usando as
alturas medidas na vista de frente, o candidato obterá em torno de 10,4
m³ o volume total da caixa d’água.
14. A figura é a planta de uma propriedade rural na escala 1/5.000. Sobre ela
podemos afirmar o que segue.
0-0) A área da propriedade é superior a 10 hectares.
1-1) O quadrilátero da planta é inscritível no círculo.
2-2) Usando estacas de cerca espaçadas de 3m, o proprietário necessita de
mais que 460 estacas para cercar todo o terreno.
3-3) O proprietário quer construir a casa eqüidistante dos quatro lados do
terreno. Isto é possível.
4-4) O maior triângulo eqüilátero inscrito no quadrilátero terá área inferior a
45.500m².
Resposta: VFVFV
Justificativa:
0-0) Verdadeira, pois uma diagonal traçada permite facilmente chegar à área
total como soma das áreas de dois triângulos, um deles retângulo. Fica
em torno de 108.700m², ou 10,87 hectares.
1-1) Falsa, pois o candidato, mesmo que desconheça a propriedade dos
quadriláteros inscritíveis, da suplementaridade de ângulos opostos ou
não perceba que o ângulo reto tem seu oposto obtuso, poderá tentar
com o compasso encontrar um circuncentro.
2-2) Verdadeira, pois o perímetro de 27,9 cm na figura acarreta 1.395m na
propriedade. Serão então necessárias 465 estacas espaçadas de 3 em 3
metros.
3-3) Falsa, pois o quadrilátero não é circunscritível ao círculo, não possuindo
incentro.
4-4) Verdadeira, pois, construindo o maior triângulo eqüilátero inscrito no
terreno, sua área tem em torno de 44.800m².
15. No mapa de uma metrópole estão representadas as avenidas (a) e (b) e uma
linha de metrô (c). Nesta, deve ser projetada uma estação, eqüidistante das
avenidas (a) e (b). Localize a posição desta estação, justificando o raciocínio
adotado.
c
a
b
Resposta:
Justificativa:
O lugar geométrico dos pontos eqüidistantes das duas avenidas é uma linha
composta de três porções distintas, mas concordantes.
A primeira é uma reta paralela às avenidas, entre os seus trechos paralelos,
que termina no ponto (A), na perpendicular tirada do ponto (C).
Segue-se um arco de parábola, que é o lugar geométrico dos pontos
eqüidistantes de C e da reta (b), que são respectivamente seu foco e sua
diretriz. Tal arco termina no ponto (B), onde a perpendicular em (C) ao
segundo trecho da avenida encontra a parábola e a bissetriz do ângulo
formado entre as avenidas (a) e (b). De (B) em diante, tal bissetriz dá
continuidade ao lugar geométrico de eqüidistância, concordando também com
a parábola em (B).
O ponto (D) em que a linha (c) atravessa o lugar geométrico, o que se dá no
seu trecho parabólico, é a solução da questão.
c
a
C
B
A
D
b
16. Um cubo deve ser cortado pelo plano diagonal (ABC) e pelo plano DEFG,
retirando-se suas porções acima desses dois planos. Represente em duas
vistas ortogonais o poliedro resultante dessas transformações, justificando o
traçado.
A
D
E
B
G
F
C
Resposta:
Justificativa:
O corte pelo plano ABC deixará o cubo com as duas vistas da figura abaixo.
O plano DEFG atinge a vista frontal com a metade do segmento GF, e a vista
superior com o aparecimento da reta de interseção dos dois planos, que vai
do ponto D ao ponto médio de GF, deixando os vistas com o aspecto final
abaixo.