Viga sobre base elástica

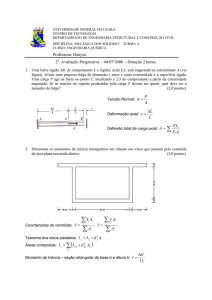
Viga sobre base elástica
Definição das variáveis para o problema de viga sobre base elástica:
k : módulo de reação da base elástica
b : largura da viga
h : altura da viga
E : módulo de elasticidade
 : tensão de tração na fibra extrema
I : momento de inércia da seção transversal
A figura seguinte mostra um elemento da viga com a convenção de sinal positivo para o
momento. O eixo z coincide com o eixo da viga. O eixo x é dado por x = y  z.
Mx  dMx
Mx
dz
z
h
b
y
Para a seção retangular com largura b e altura h, o momento de inércia da seção
transversal é dado por:
I 
bh3
12
A tensão normal à seção transversal da viga, supondo material elástico e linear, pode ser
escrita como:
z 
Mx z
y
I
As tensões críticas na seção transversal ocorrem nas fibras extremas.
Tensão na fibra inferior:
z  
6
Mx z
bh2
Tensão na fibra superior:
z  
6
Mx z
bh2
Força concentrada aplicada em uma viga infinita
Considerando uma força concentrada P aplicada na origem dos eixos e no sentido do eixo
y, a expressão para o momento fletor numa viga infinita pode ser escrita como:
Mx z 
P z
e cos z  sin z
4
Onde:
1
3k 4
   3 
 Eh 
O ponto de momento máximo ocorre em z = 0. Portanto, o momento máximo pode ser
escrito como:
Mx 
P
4
Substituindo o momento máximo na expressão da tensão na fibra inferior, a máxima
tensão de tração pode ser escrita como:
3
4
1
3 P  E 4
 


2 b  kh5 
Raio de rigidez relativa
Raio de rigidez relativa é a distância a partir do ponto de aplicação da força concentrada
até o primeiro ponto de tensão nula. Essa distância pode ser determinada igualando a
expressão do momento a zero.
Mx z  0
P z
e cos z  sin z  0
4
cos z  sin z  z 


 z 
4
4
1
 Eh3  4
z  0.59677 

 k 
Por distância relativamente longe da borda entende-se uma distância não inferior ao raio
de rigidez relativa.
Força concentrada aplicada em uma viga semi-infinita
Considerando uma força concentrada P aplicada na origem dos eixos e no sentido do eixo
y, a expressão para o momento fletor numa viga semi-infinita (z  0) pode ser escrita
como:
P z
e sin z

Mx z  
Onde:
1
3k 4
   3 
 Eh 
O ponto de momento mínimo na viga pode ser determinado pelo seguinte:
dMx

 0  Pez cos z  sin z  0  z 
dz
4
Observe que essa distância z é igual ao raio de rigidez relativa. Portanto, o momento
mínimo pode ser escrito como:
Mx  
P  4 2
e

2
Substituindo o momento mínimo na expressão da tensão na fibra superior, a máxima
tensão de tração pode ser escrita como:
3
4
  3

2e

4
1
P  E 4


b  kh5 
A distância a partir do ponto de aplicação da força concentrada até o primeiro ponto de
tensão nula pode ser determinada igualando a expressão do momento a zero.
Mx z  
P z
e sin z  0

sin z  0  z    z 


Observe que essa distância z é igual a quatro vezes o raio de rigidez relativa.
Modelo para força por unidade de comprimento
Considere uma viga imaginária de largura b, no interior de uma laje que está sujeita a
uma força por unidade de comprimento w, conforme mostrado na figura seguinte.
força/comprimento = w
viga imaginária
b
P  wb
z
y
A força concentrada que está aplicada na viga imaginária de largura unitária é dada por:
P  wb
A seguir serão apresentadas duas possibilidades de posicionamento da força por unidade
de comprimento, sendo uma relativamente longe da borda e outra relativamente perto da
borda da laje.
Força por unidade de comprimento longe da borda
Considerando a expressão obtida para o caso de força concentrada aplicada em uma viga
infinita, pode ser escrito:
1
E 4
P  wb    1.1398w  5 
 kh 
A máxima tensão de tração ocorre diretamente sob a linha de aplicação da força por
unidade de comprimento, na face inferior da placa.
Força por unidade de comprimento perto da borda
Considerando a expressão obtida para o caso de força concentrada aplicada em uma viga
semi-infinita, pode ser escrito:
1
E 4
P  wb    1.4698w  5 
 kh 
A máxima tensão de tração ocorre a uma distância igual ao raio de rigidez relativa a partir
da linha de aplicação da força por unidade de comprimento, na face superior da placa. A
distância a partir da linha de aplicação da força por unidade de comprimento até o
primeiro ponto de tensão nula é igual a quatro vezes o raio de rigidez relativa.
Exercício 1: Laje sobre solo, com espessura igual a 10 cm, na forma retangular com
lados medindo 300 cm x 450 cm. O módulo de reação do solo é igual a 5.54 kgf/cm3. A
resistência à compressão do concreto é igual a 250 kgf/cm2. Considerando fator de
segurança igual a 2, qual o máximo peso por unidade de comprimento de uma parede
longe das bordas que a laje pode suportar?
Exercício 2: Laje sobre solo, com espessura igual a 10 cm, na forma retangular com
lados medindo 300 cm x 450 cm. O módulo de reação do solo é igual a 5.54 kgf/cm3. A
resistência à compressão do concreto é igual a 250 kgf/cm2. Considerando fator de
segurança igual a 2, qual o máximo peso por unidade de comprimento de uma parede
perto das bordas que a laje pode suportar?