Ficha Nº 8

Escola Secundária de Fontes Pereira de Melo - 401780
"Escola em processo de mudança"
Ano Lectivo
2011/2012
FICHA DE TRABALHO
NOME: ____________________________________ ; Nº_____
Matemática
12º
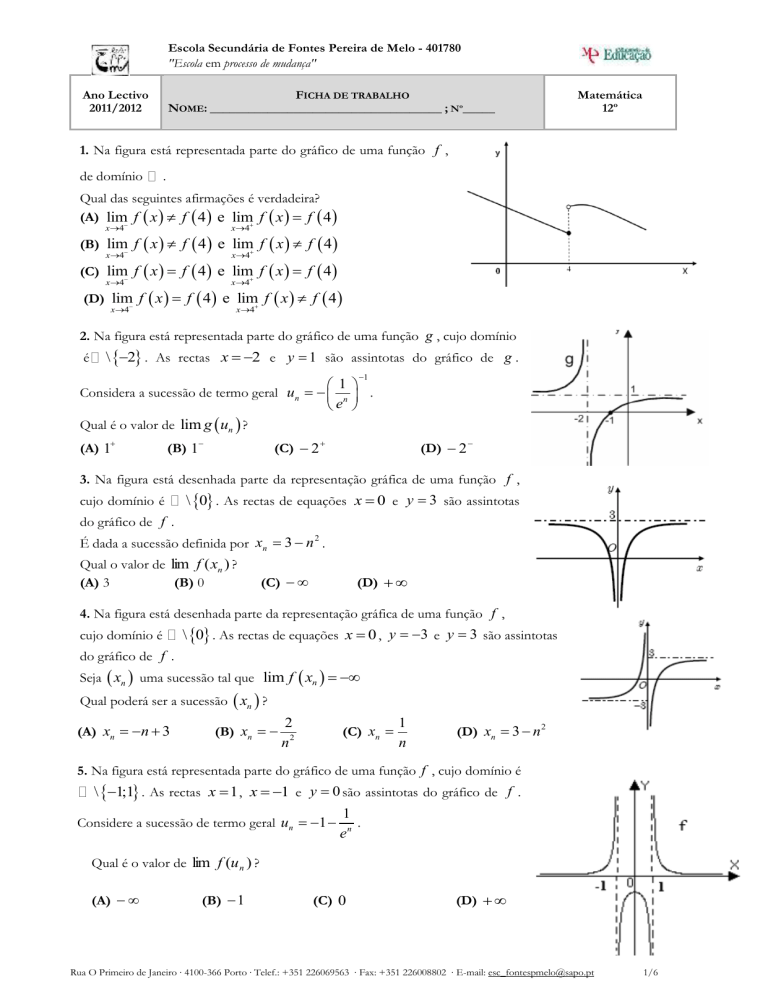
1. Na figura está representada parte do gráfico de uma função f ,
de domínio
.
Qual das seguintes afirmações é verdadeira?
(A) lim f  x   f  4 e lim f  x   f  4 
x4
x4
x4
x4
x4
x4
(B) lim f  x   f  4 e lim f  x   f  4 
(C) lim f  x   f  4 e lim f  x   f  4 
(D) lim f  x   f  4 e lim f  x   f  4 
x4
x4
2. Na figura está representada parte do gráfico de uma função g , cujo domínio
é
\ 2 . As rectas x  2 e y  1 são assintotas do gráfico de g .
1
1
Considera a sucessão de termo geral un    n  .
e 
Qual é o valor de lim g  un  ?
(A) 1
(B) 1
(C)  2 
(D)  2 
3. Na figura está desenhada parte da representação gráfica de uma função f ,
cujo domínio é
\ 0 . As rectas de equações x  0 e y  3 são assintotas
do gráfico de f .
É dada a sucessão definida por xn  3  n 2 .
Qual o valor de lim f ( xn ) ?
(A) 3
(B) 0
(D)  
(C)  
4. Na figura está desenhada parte da representação gráfica de uma função f ,
cujo domínio é
\ 0 . As rectas de equações x  0 , y  3 e y  3 são assintotas
do gráfico de f .
Seja  xn  uma sucessão tal que lim f  xn   
Qual poderá ser a sucessão  xn  ?
(A) xn  n  3
(B) xn  
2
n2
(C) xn 
1
n
(D) xn  3  n 2
5. Na figura está representada parte do gráfico de uma função f , cujo domínio é
\ 1;1 . As rectas x  1 , x  1 e y  0 são assintotas do gráfico de f .
1
Considere a sucessão de termo geral un  1  n .
e
Qual é o valor de lim f (u n ) ?
(A)  
(B)  1
(C) 0
(D)  
Rua O Primeiro de Janeiro ∙ 4100-366 Porto ∙ Telef.: +351 226069563 ∙ Fax: +351 226008802 ∙ E-mail: [email protected]
1/6
n
1
 xn  a sucessão de termo geral xn  1   . Seja
 n
yn  1  ln  xn  . Qual é o valor de lim yn ?
6.Seja
(A) 2
 yn 
a sucessão de termo geral
(C) 1  e
(B) 3
(D) 2  e
7. Na figura ao lado está parte da representação gráfica de uma função f ,
par e positiva, da qual a recta de equação y  0 é assintota.
Qual é o valor de lim
x 
(A) 0
1
?
f  x
(C) 
(B) 1
(D) 
8. Na figura está parte da representação gráfica de uma função h de domínio
Considera as sucessões un 
e contínua em
\ 0 .
2
e vn  2  n 2 .
n
Qual das afirmações seguintes é verdadeira.
(A) lim h  un   1 e lim h  vn   0
(B) lim h  un   2 e lim h  vn   h  2 
(C) lim h  un   1 e lim h  vn   
(D) lim h  un   2 e lim h  vn   0
9.Sejam f  x  
x3
x3  1
e g  x 
funções reais de variável real. Considere L1  lim f  x  e
2
x 
x2
2  x
L2  lim g  x  . Então podemos afirmar que:
x 2
(A) L1   e L2  
(B) L1   e L2  
(C) L1   e L2  
(D) L1   e L2  
10.Seja f a função definida por f ( x) 
x3  6 x 2  11x  6
, de domínio
x2  2 x  1
\ 1 .
Resolve as seguintes alíneas utilizando métodos exclusivamente analíticos. Calcula:
10.1. lim f ( x)
10.2. lim f ( x )
x 
x 1
11. Calcula os seguintes limites:
11.1.
x 
 x
lim  
 2

x  1  x  1
x 1
11.3. lim
t 
t
2
 3  t 2 1

1
t
11.2. lim  
t 0
11.4. lim
x 2
1 

t 1
2
x 2  7  8x  5
x2
Rua O Primeiro de Janeiro ∙ 4100-366 Porto ∙ Telef.: +351 226069563 ∙ Fax: +351 226008802 ∙ E-mail: [email protected]
2/6


12. Seja i  x   log 1  2 x . O domínio de i é:
(A)

(B)

0

(C)


0
(D)

13. Seja g uma função, de domínio A , definida por g  x   ln 1  x 2 . Qual dos seguintes conjuntos poderá ser
o conjunto A ?
(A) 0, 
(C) e  1, e  1
(B) ,1
(D) 1,1
14.Sejam a , x e y três números reais tais que log a x  1  5log a y . Qual das igualdades seguintes é
necessariamente verdadeira?
(B) x  5ay
(A) x  ay 5

(C) x  5 y
(D) x  y 5

15. Seja m( x)  ln e 3 x . Qual das seguintes expressões pode também definir a função m ?
(A) e  ln 3 x
(B) e  ln 3 x
(C)
1
2
(B)
3
2
C)
(D)
1  ln x
2
1
:
e
16. Indique o número real que é solução da equação e x  2 
(A)
3  ln x
3
5
2
(D)
7
2
17. No referencial da figura está parte do gráfico de uma função h
definida por h  x   log a x, a  1 e um triângulo  ABC  .
Sabe-se que:
 O vértice C do triângulo pertence ao gráfico de h ;
 A   a , 0 e B   3a , 0  ;
 AC  BC .
As coordenadas do ponto C são:
a

, 1  log a 2 
2


 3a

, log a 2 
(C) C  
 2

(A) C  
(B) C   2a , loga 2
(D) C   2a ,1  log a 2 
18.As substâncias radioactivas desintegram-se, com o decorrer do tempo, de acordo com a lei M  Ae  kt , sendo
A a quantidade inicial, M a quantidade existente decorrido o tempo t e k uma constante positiva que depende
da substância em causa. Uma amostra de 10mg de rádio desintegra-se segundo a lei:
M  t   10e kt , sendo t o tempo expresso em milhares de anos
18.1. Sabendo que decorridos 400 anos a massa da amostra se reduz a 8, 43mg , verifica que, com três casas
decimais, se tem k  0, 427
18.2. Chama-se período de semidesintegração ao tempo necessário para que uma substância radioactiva se reduza
a metade. Determina, em anos com aproximação às unidades, o período de semidesintegração do rádio.
19.Admite que o número de habitantes de um certo país é dado por:
N t  
100
com N expresso
1  9  e 0,18t
em milhões e sendo t, o número de anos contado desde o início do ano 2000.
19.1. Determina o número de habitantes do referido país em 2000.
19.2. Passado quanto tempo (em mês e ano) a população duplicou?
Rua O Primeiro de Janeiro ∙ 4100-366 Porto ∙ Telef.: +351 226069563 ∙ Fax: +351 226008802 ∙ E-mail: [email protected]
3/6
19.3. Em que ano serão atingidos os 45 milhões de habitantes?
19.4. A longo prazo, quantos habitantes terá, presumivelmente o país, se aquele modelo continuar válido?
20. Na figura abaixo estão representadas, em referencial o. n. xOy .
• parte do gráfico da função f , de domínio
• parte do gráfico da função
O ponto A é o ponto de
intersecção do gráfico de g
Na figura está também
CDE  .
, definida por f ( x)  e x

, definida por g ( x)  ln x
intersecção do gráfico de f com o eixo Oy e o ponto B é o ponto de
com o eixo Ox .
representado um triângulo
g , de domínio
O ponto C pertence ao eixo Oy , o ponto D pertence
ao gráfico de f e o ponto E pertence ao gráfico de g .
Sabe-se ainda que:
• a recta BD é paralela ao eixo Oy e a recta CE é paralela
ao eixo Ox
• AC  OA
Qual é a área do triângulo CDE  ?
21. Na figura estão parcialmente representados os gráficos de duas funções
polinomiais, r e s
Qual dos seguintes conjuntos pode ser o domínio da função
(A)
\ 0
(B)
(C)
\ 1,1
r
?
s
(D)
\ 1,0,1
22. De uma função h sabe-se que:
O domínio de h é
lim h  x   0

x 
lim h  x   
x 0
Indica qual dos gráficos seguintes poderá ser o gráfico de h
23. Seja f uma função de domínio
(A) 0,3
e contradomínio  3, 2 . Qual será o contradomínio de f ?
(C)  2,3
(B) 0, 2
(D)  2,3
24. Na figura está representada parte do gráfico de uma função f , polinomial do
terceiro grau. 2 é um máximo relativo da função f . Seja g a função de domínio
, definida por g  x   f  x   2 .
Quantos são os zeros da função g
(A) quatro
(B) três
(C) dois
(D) um
Rua O Primeiro de Janeiro ∙ 4100-366 Porto ∙ Telef.: +351 226069563 ∙ Fax: +351 226008802 ∙ E-mail: [email protected]
4/6
25. Considera num referencial o. n. 0xyz , uma pirâmide quadrangular regular, de altura
1, cuja base está contida no plano xoy . Para cada c  0,1 , seja V  c  o volume da
parte da pirâmide constituída pelos pontos cuja cota é superior ou igual a c .
Qual dos gráficos seguintes pode ser o da função V ?
(A)
(B)
(C)
(D)
26.Na figura junta está representado o círculo trigonométrico. Considera que um
ponto P parte de A 1,0  e se desloca sobre a circunferência, dando uma volta
completa, em sentido contrário ao dos ponteiros do relógio. Para cada posição do
ponto P , seja x a amplitude, em radianos, do ângulo orientado cujo lado origem é a
semi-recta OA e cujo lado extremidade é a semi-recta OP ( x   0, 2  )
Seja g a função que, a cada valor de x , faz corresponder a área da região sombreada
(região limitada pelos segmentos de recta OP ,  PA e
função g ?
(A)
(B)
 AO ). Qual dos seguintes gráficos pode ser o da
(C)
(D)
27.Na figura estão representadas:
 Uma circunferência de raio 1
 Uma recta r , tangente à circunferência no ponto A
Admite que um ponto P , partindo de A , se desloca sobre a circunferência, em sentido
contrário ao dos ponteiros do relógio, descrevendo uma única volta em sessenta
segundos.
Seja d  t  a distância do ponto P à recta r , t segundos após o início do movimento.
Qual dos gráficos seguintes pode ser o da função d ?
(A)
(B)
(C)
(D)
Rua O Primeiro de Janeiro ∙ 4100-366 Porto ∙ Telef.: +351 226069563 ∙ Fax: +351 226008802 ∙ E-mail: [email protected]
5/6
28. Na figura está representado um cubo, em referencial o. n. 0xyz . Três das
arestas do cubo estão contidas nos eixos do referencial. Os pontos P e Q são
dois vértices do cubo, pertencentes ao plano y 0 z . Admite que um ponto R ,
partindo da origem do referencial, se desloca ao longo do semieixo positivo 0z .
Seja g a função que faz corresponder, à abcissa x do ponto R , a área da
secção produzida no cubo pelo plano PQR .
Qual dos seguintes pode ser o gráfico da função g ?
(A)
(B)
(C)
(D)
29. Na figura está representado, em referencial o. n. 0xyz um cilindro de
revolução. Tem-se que:
 a altura do cilindro é 3
 uma das bases está contida no plano x 0 y , sendo o seu centro o ponto
 0,1,0 e o seu raio igual a 1
Seja b  0, 2 e seja f a função que, a cada valor de
b , faz corresponder o
perímetro da secção produzida no cilindro pelo plano y  b .
Qual é o máximo da função f ?
(A) 9
(B) 10
(C) 11
(D) 12
30. Um tanque tem a forma de um paralelepípedo retângulo, com 7m de comprimento, 5m de largura e 4m
de altura. Admite que o tanque está vazio. Num certo instante, é aberta uma torneira que verte água para o
tanque, à taxa de 2m3 por hora, até ficar cheio.
Qual é a função que dá a altura, em metros, da água no tanque, t horas após a abertura da torneira?
(A) h  t   4  2t , t  0,70
(C) h  t   4  2t , t  0,140
2t
, t   0, 70
35
2t
, t   0,140
(D) h  t  
35
(B) h  t  
Rua O Primeiro de Janeiro ∙ 4100-366 Porto ∙ Telef.: +351 226069563 ∙ Fax: +351 226008802 ∙ E-mail: [email protected]
6/6