Exercicio 1- Exercicio 22 do Speigel (pag

EXERCÍCIOS - ANÁLISE VETORIAL EM FÍSICA ( 1o PARTE )
Ex 1 – Exercício 58 do Spiegel (pag. 21).
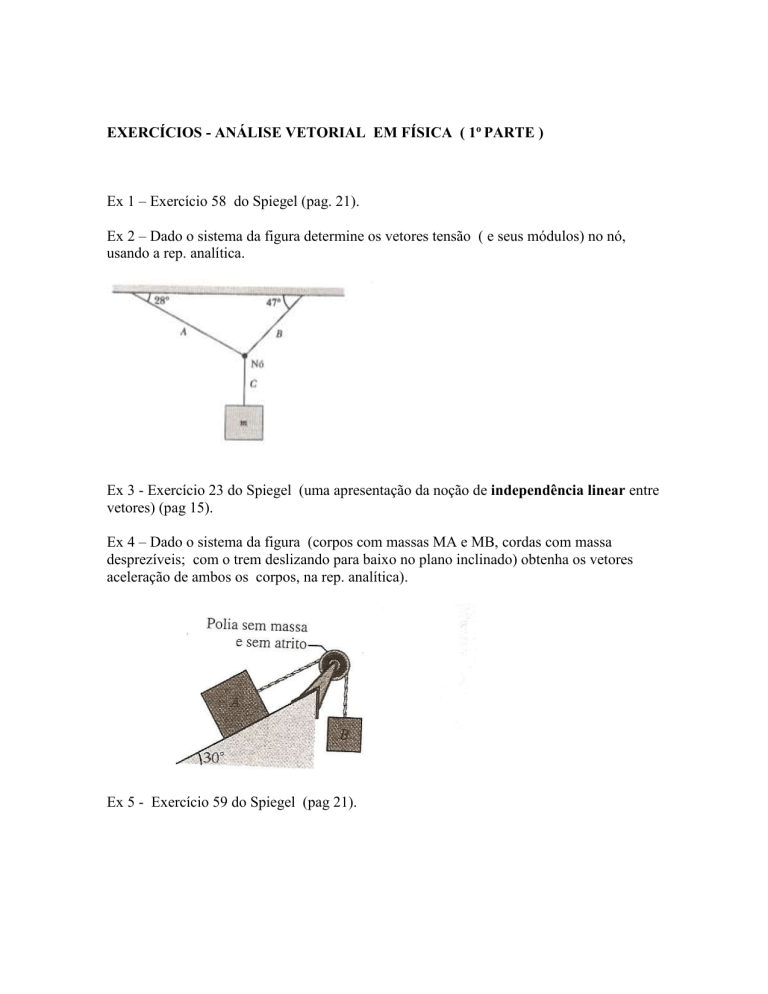
Ex 2 – Dado o sistema da figura determine os vetores tensão ( e seus módulos) no nó,
usando a rep. analítica.
Ex 3 - Exercício 23 do Spiegel (uma apresentação da noção de independência linear entre
vetores) (pag 15).
Ex 4 – Dado o sistema da figura (corpos com massas MA e MB, cordas com massa
desprezíveis; com o trem deslizando para baixo no plano inclinado) obtenha os vetores
aceleração de ambos os corpos, na rep. analítica).
Ex 5 - Exercício 59 do Spiegel (pag 21).
Ex 6 - Exercícios 9 e 10 do Spiegel (pag 27).
Ex 7 - Exercícios 55, 56 e 65 do Spiegel (pag 42).
Ex 8 - Exercícios 78 e 79 do Spiegel (pag 44).
Ex 9 - Exercício 47 do Spiegel (pag 38).
Ex 10 - Um corpo se movimenta na diagonal principal do plano xy, num percurso total de
comprimento L. Uma das forças atuando nesse corpo tem a forma F= -3i+j+2k . Obtenha o
trabalho realizado por essa força.
Ex 11 - Considere uma partícula de massa m. Num certo instante são dados os vetores:
velocidade
V = 3 i - 5 j (m/s) ; posição R = -i + 2 j -3k (m); força total F = 2i + 4 j (N).
Determine: a) o ângulo que o vetor R faz com o vetor V b) o vetor momento angular L
do corpo c) o ângulo que o vetor R faz com o vetor L d) o módulo de L e) o vetor
torque T atuando sobre o corpo f) o seu módulo.
Ex 12 – Considere uma partícula em movimento circular uniforme (trajetoria de raio R,
vetor velocidade angular w=w0k). Obtenha o vetor velocidade num certo instante e mostre
que é perpendicular ao vetor posição da partícula nesse instante. Calcule também o vetor
momento angular da partícula nesse instante.
Ex 13 - Exercício 31 do Spiegel (pag 73).
Ex 14 - Exercício 33 do Spiegel (pag 74).
Ex 15 - Uma partícula (sujeita exclusivamente ao campo gravitacional terrestre) é lançada
da origem do sistema de coordenadas com vetor velocidade inicial dado. a) determine os
vetores posição, velocidade e aceleração em função do tempo b) prove que a trajetória da
partícula é uma parábola.
Ex 16 - Mesmo sistema do Ex 19. Obtenha o “tempo de voo” T do projétil. Determine o
vetor posição e o vetor velocidade da partícula em T.
Ex 17 - O potencial gravitacional de um corpo celeste é dado pela função W(x,y,z) = a/x +
b/y +c/z – d(xyz), onde a,b,c,d são constantes. Se as derivadas parciais de W em relação a
cada coordenada são proporcionais ás componentes da força gravitacional F em cada ponto
determine a) F(x,y,z) b) F(3,4,-1).
Ex 18 - Exercício 43 do Spiegel (pag 75).
Ex 19 - Exercício 44 do Spiegel (pag 75).
Ex 20 - Exercício 32 do Spiegel (pag 73).
Ex 21- Exercício 34 do Spiegel (pag 74).
Ex 22 - Considere uma partícula em M.C.U.A. Sao dados : a massa da particula (Mo) a
“aceleração angular” (ctee o raio do circulo (R). Obtenha os vetores posição,
velocidade, aceleração, e torque em relação ao centro do círculo (e seus respectivos
modulos) no instante t=3s.