Valter Bezerra Dantas Geometria Analítica e Vetores Atualidade e

Valter Bezerra Dantas
Geometria Analítica e Vetores
Atualidade e Simplicidade no Ensino da
Geometria
8. Vetores unitários, fatoração de vetores.
As funções trigonométricas, como seno e co-seno foram inicialmente definidas para
ângulos agudos que correspondiam aos ângulos menores de triângulos retângulos.
O seno do ângulo corresponde, no tal triângulo retângulo, a razão entre a medida do
cateto oposto ao ângulo considerado e a medida da hipotenusa, para o cosseno emprega
como numerador a medida do cateto adjacente. O seno e o cosseno são números reais
positivos entre zero e um que devem obedecer à relação fundamental cos2θ + sen2θ = 1,
conseqüência do teorema de Pitagoras.
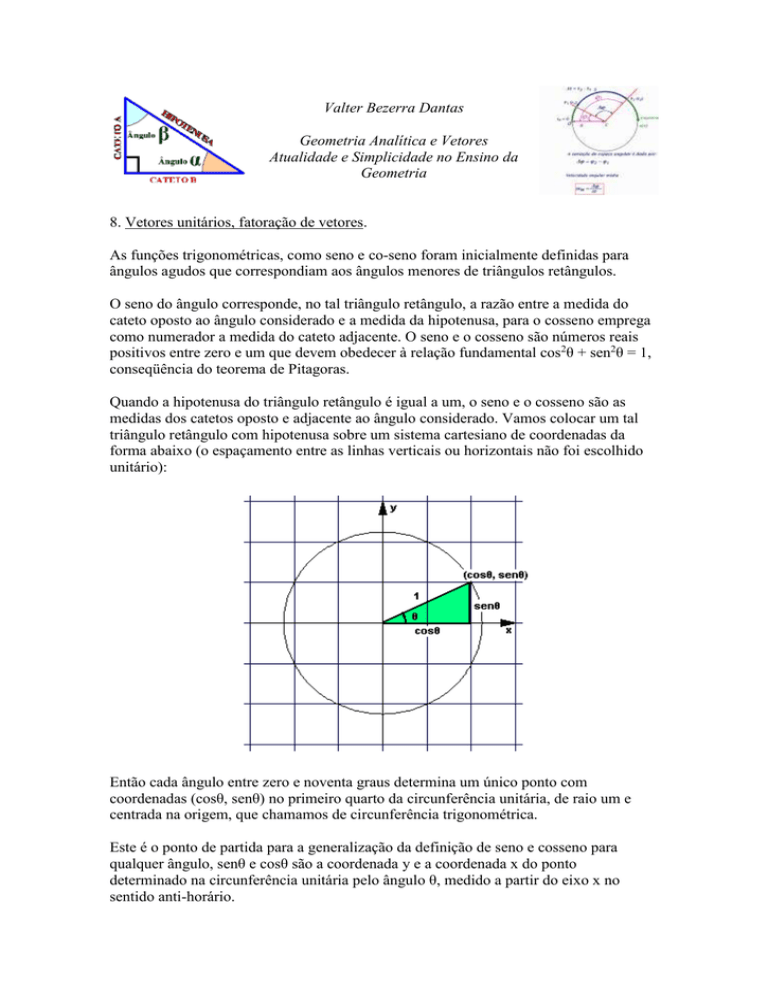
Quando a hipotenusa do triângulo retângulo é igual a um, o seno e o cosseno são as
medidas dos catetos oposto e adjacente ao ângulo considerado. Vamos colocar um tal
triângulo retângulo com hipotenusa sobre um sistema cartesiano de coordenadas da
forma abaixo (o espaçamento entre as linhas verticais ou horizontais não foi escolhido
unitário):
Então cada ângulo entre zero e noventa graus determina um único ponto com
coordenadas (cosθ, senθ) no primeiro quarto da circunferência unitária, de raio um e
centrada na origem, que chamamos de circunferência trigonométrica.
Este é o ponto de partida para a generalização da definição de seno e cosseno para
qualquer ângulo, senθ e cosθ são a coordenada y e a coordenada x do ponto
determinado na circunferência unitária pelo ângulo θ, medido a partir do eixo x no
sentido anti-horário.
Esta definição serve tanto para ângulos positivos quanto negativos, sendo os ângulos
negativos medidos a partir do eixo x no sentido anti-horário. Também serve para
ângulos maiores do que 360°, entendo que damos mais do que uma volta completa ao
determinar o ângulo a partir do eixo x. É natural que a identificação que fazemos, entre
ângulos que diferem por múltiplos de 360°.
Agora seno e cosseno são números reais positivos ou negativos, com módulo entre zero
e um, satisfazendo a relação fundamental cos2θ + sen2θ = 1, que indica a pertinência do
ponto (cosθ,senθ) à circunferência unitária ou trigonométrica. Percebamos como a
trigonometria, com a definição moderna de seno e cosseno, fica naturalmente ligada à
geometria analítica. Não cansamos de ressaltar que este esboço da apresentação da
geometria que aqui propomos pressupõe um trabalho anterior ou paralelo com
trigonometria.
Associamos cada ângulo θ ao ponto P(θ)=(cosθ,senθ) da circunferência trigonométrica,
a este ponto associamos o seu vetor de posição u(θ)=<cosθ,senθ>. Este vetor, aplicado à
origem (0,0) do sistema de eixos, a leva ao ponto P(θ).
Dizemos que um vetor é unitário quando tem norma igual a 1, um vetor unitário agindo
na origem do sistema de eixos sempre leva este ponto até a circunferência
trigonométrica, todo vetor unitário tem a forma
u(θ) = <cosθ, senθ>,
sendo determinado pelo seu ângulo de direção θ. Para θ = 0º, u(θ) = <1,0>, para θ = 30º,
u(θ) = <√3/2,1/2>, para θ ~ 36,87º, u(θ) = <4/5,3/5>, para θ = 45º, u(θ) = <√2/2,√2/2>,
para θ ~ 53,13º, u(θ) = <3/5,4/5>, para θ = 60º, u(θ) = <√3/2,1/2>, para θ = 90º, u(θ) =
<0,1>.
Notamos que temos um e somente um vetor unitário para cada direção possível.
Valter Bezera Dantas
Consideremos um vetor não nulo v = <a,b>, escrevendo a = ||v|| cosθ, b = ||v|| senθ,
temos:
v = <a,b> = <||v|| cosθ, ||v|| senθ> = ||v|| <cosθ, senθ>,
isto é v = ||v|| u(θ).
Desta forma um vetor qualquer pode ser escrito como o produto escalar do seu módulo
||v|| por um vetor unitário u(θ) = <cosθ, senθ>, cujas componentes são o cosseno e seno
de sua direção.
Interpretamos a expressão v = ||v|| u(θ) como uma fatoração do vetor v, o primeiro fator
carrega a informação sobre o módulo, o segundo fator carrega a informação sobre a
direção e sentido. Se v e u(θ) agem na origem do sistema de eixos como acima, u(θ)
leva (0,0) no ponto (cosθ,senθ) da circunferência trigonométrica.
Esta fatoração do vetor com módulo vezes vetor unitário é por vezes de interesse
prático, quando a efetuamos para a velocidade vetorial de um automóvel, escrevendo v
= ||v|| u(θ), somos levados a interpretações interessantes.
Em movimento retilíneo, quando aceleramos, o velocímetro mostra as variações no
módulo da velocidade, ||v|| aumenta, porém u(θ) permanece constante. Já no movimento
circular uniforme, o velocímetro não mostra qualquer variação e ||v|| é constante, porém
o vetor velocidade varia, dado que u(θ), tal qual a direção θ da velocidade, varia ao
longo da curva.
Valter Bezerra Dantas
Geometria Analítica e Vetores
Atualidade e Simplicidade no Ensino da Geometria
9. A rotação de vetores de 90° nos sentidos horário (direita) e anti-horário (esquerda,
volver!).
Dizemos que o vetor w é uma rotação por um
ângulo α do vetor v quando w tem o mesmo módulo
do vetor v, ||w||=||v||, porém tem um ângulo de
direção θ + α, que corresponde ao ângulo de direção
de v adicionado de α (se α é positivo dizemos que a
rotação é anti-horária, se é negativo, que a rotação é
horária). Para rodar um vetor, basta obter seu
módulo e sua direção, manter o módulo e adicionar
o ângulo pretendido na direção.
Nos preocuparemos neste tópico com rotações α = 90° (no sentido anti-horário) e α = 90°, no sentido horário.
Para estes casos particulares o diagrama abaixo, com bandeirinhas, nos permite, a partir
das componentes do vetor inicial v, concluir rapidamente quais são as componentes do
vetores w e w', resultados das rotações horárias e anti-horárias de v.
Reparem, caros colegas, que este argumento intuitivo, especializado no caso de vetores
com módulo unitário, é o que empregaríamos para explicar a um estudante que
cos(θ+90°) = -sen(θ), sen(θ+90°) = cos(θ), cos(θ-90°) = sen(θ), sen(θ-90°)= -cos(θ).
Pelas bandeirinhas vemos que a partir das componentes de v=<a,b>, obtemos as
componentes da sua rotação de 90° no sentido anti-horário, w=<-b,a> trocando as
componentes de ordem, mas trocando o sinal da segunda, que vai para o lugar da
primeira. Analogamente obtemos sua rotação de 90° no sentido horário w'=<b,-a>,
trocando as componentes de ordem, mas trocando o sinal da primeira, que vai para o
lugar da segunda.
Historicamente, o primeiro sistema vetorial conhecido foi o dos números complexos, o
complexo z=a+ib era interpretado como o vetor v=<a,b>. Notem que então a rotação de
+90° corresponde a multiplicar o complexo z por +i, enquanto que a rotação de -90°
corresponde a multiplicar o complexo z por -i. De fato,
i (a+ib) = -b+ia, -i (a+ib) = b - ia.
Assim sendo, desde o início do trabalho com vetores, os amantes destas setas sabem
girá-las de 90° e esta ferramenta pode ser muito útil.
12.1 Área, determinantes 2x2 e produto de Grassmann entre vetores, origem histórica da
regra de Cramer.
Começamos por considerar dois vetores, A = a1 i + a2 j, B = b1 i + b2 j, com direção
entre zero e 90 graus, sendo a direção de A menor do que a direção de B. Imaginemos
que A age na origem (0,0) do sistema de eixos, deslocando este ponto até (a1,a2), em
seguida B age neste último ponto, deslocando-o até o ponto (a1+b1,a2+b2), imaginemos
também as ações efetuadas na ordem oposta, primeiro B age em (0,0) levando-o em
(b1,b2), em seguida age A, levando este último em (a1+ b1, a2+ b2).
Desenhando as representações destas quatro ações temos o paralelogramo em que
sempre pensamos ao efetuar a soma vetorial de duas forças representadas por A e B. A
soma vetorial A+B desloca o ponto (0,0) diretamente ao ponto final (a1+ b1, a2+ b2).
A área deste paralelogramo cujos lados estão naturalmente associados às ações de A e B
é igual a área de um retângulo, menos a área de dois triângulos retângulos, menos a área
de dois trapézios.
A(ret) = (a1+ b1) (a2+ b2) = a1a2 + a1b2 + b1a2 + b1b2,
A(trg1) = (½) (a1a2), A(trg2) = (½) ( b1b2),
A(trp1) = {(½) (a2 + (a2 + b2))} b1 = a2b1 + (½) (b2b1),
A(trp2) = {(½) (b1 + (a1 + b1))} a2 = b1a2 + (½) (a1a2),
subtraindo da primeira área as quatro seguintes, eliminamos os fracos, sobrevivem
apenas os fortes, daí temos para a área do paralelogramo:
A(paralelogramo) = a1b2 - a2 b1,
o interessante é que coincide com o determinante de uma matriz dois por dois cujas
colunas ou linhas são dadas pelas componentes dos dois 'vetores-lados' dos
paralelogramo.
Podemos pensar em uma operação com vetores em que, a partir dos vetores A=a1i+a2j
e B=a1i+a2j, a operação retorna como resultado o número real A*B=a1b2-a2b1,
correspondente ao determinante da matriz dois por dois na qual os vetores A e B são as
colunas, ou da matriz em que estes vetores são as linhas. Chamamos esta operação de
produto asterisco de dois vetores, denotamos seu resultado por A*B.
Seria mais correto denominar esta operação com vetores de produto de Grassmann, este
grande matemático, que inventou o tal produto, afirmou em notas auto-biográficas que o
teria inventado a partir de uma sugestão que seu pai lhe havia feito quando era apenas
estudante (vide E. Crowe, A History of Vector, Analysis, Dover). Dado que o
Grassmann está morto mesmo, iremos chamar o produto de produto asterisco.
O produto asterisco tem várias propriedades que podemos demonstrar a partir da sua
definição, as duas primeiras propriedades na tabela abaixo reafirmam a anti-simetria do
produto asterisco, se pensamos no determinante, a primeira correspondente à troca de
sinal do determinante, quando trocamos suas linhas (ou colunas), a segunda ao fato de
que um determinante se anula quando tem linhas iguais.
As propriedades três e quatro mostram compatibilidade entre o produto asterisco e
outras duas operações com vetores, a soma e o produto por escalar, este produto pode
ser distribuído com relação à soma vetorial tanto à direita quanto à esquerda,
enunciamos apenas tal propriedade à direita, mas dada a anti-simetria do produto,
também vale à esquerda. Os escalares transitam à vontade no produto, podem passar de
A para B ou serem colocados em evidência.
Propriedades do produto asterisco (a1b2a2b1)
A*B= -B*A (anti-simetria)
A*A=0 (quadrado igual a zero)
A*(B+C)=A*B+A*B (bi-linearidade)
(λA)*(B)=(A)*(λB)=λ(A*B) (bilinearidade)
|A*B| = ||A|| ||B|| senθ (significado
geométrico)
Quanto à última das propriedades, afirma que o módulo do determinante ou produto
asterisco coincide com o produto dos módulos dos vetores envolvidos vezes o seno do
ângulo entre eles.
Concluiremos que no cálculo de área que fizemos mais acima, já tínhamos mostrado a
quinta propriedade para um caso particular, aquele em que as direções dos vetores
envolvidos no produto variavam entre zero e noventa graus e que a direção de B era
maior do que a de A.
Antes, comentamos que o ângulo que aparece na quinta propriedade é o que chamamos
de ângulo entre os vetores A e B.
O ângulo entre dois vetores é definido como o menor ângulo entre as representações dos
dois vetores quando estas partem de um mesmo ponto inicial. Este é o ângulo que
empregamos para escrever a área de um triângulo como metade do produto entre os
lados multiplicado pelo seno do ângulo entre eles, em nosso caso estes lados
correspondem às representações dos vetores A e B.
Notem que o paralelogramo cuja área calculamos mais acima tem o dobro da área do
triângulo com lados ||A|| e ||B||. Portanto, ao obter que a área do paralelogramo era dada
pelo determinante, obtivemos que
a1b2-a2b1 = ||A|| ||B|| senθ.
isto é, a quinta propriedade em um caso particular.
Entretanto reparem que se trocamos os vetores de ordem o determinante troca de sinal
enquanto que a área não. Por conseguinte a prova que fizemos, foi apenas para um caso
particular, não vale em geral.
Para ver o que dá o determinante em geral, consideraremos as normas e as direções dos
vetores A e B.
O que faremos é fatorar cada vetor como o produto do seu módulo pelo vetor unitário
que indica sua direção, tendo feito isto escrevemos o seu produto asterisco e
empregamos a fórmula do seno da diferença.
Para tanto sejam α e β as direções dos dois vetores, então, fatorando-os:
a1= ||A|| cosα e a2= ||A|| senα,
b1= ||B|| cosβ e b2= ||B|| senβ,
daí calculamos o determinante diretamente:
a1b2 - a2b1 = ||A||cosα ||B||senβ - ||A||senα ||B||cosβ = ||A|| ||B|| sen(β-α),
empregamos a fórmula para obter esta expressão, que veremos, implicará na
propriedade da quinta linha da tabela.
Repare que a diferença β-α entre as direções dos dois vetores está relacionada, mas não
é exatamente igual ao ângulo θ entre eles.
Temos neste momento duas fórmulas:
|A*B| = ||A|| ||B|| senθ (I)
A*B = ||A|| ||B|| sen(β-α) (II)
a primeira delas foi a afirmada na tabela, queremos prová-la. A segunda delas foi a que
obtivemos com a fatoração dos vetores e a aplicação da lei do seno da diferença. A
segunda dá o valor exato do produto asterisco com sinal, a primeira delas dá apenas o
módulo deste produto.
São fórmulas diferentes, θ é o menor ângulo entre os vetores e β - α é a diferença entre a
direção do segundo e do primeiro vetores envolvidos no produto. Para mostrar que (II)
implica em (I), basta notarmos que temos quatro possibilidades,
(i) β > α e β - α <180°, neste caso β - α = θ, a diferença de direções coincide com o
menor ângulo,
(ii) β > α e β - α >180°, neste caso β - α = 360° - θ, mas ainda assim senθ = |sen(β-α)| e
(I) implica em (II),
(iii) α > β e α - β <180°, neste caso α - β = θ, portanto senθ = sen(α-β) = |sen(β-α)| e (I)
implica em (II),
(iv) α > β e α - β >180°, neste caso α - β = 360° - θ, portanto senθ = sen(β-α),
terminando a prova.
Fica estabelecida a validade em geral da fórmula I, como conseqüência da fórmula II,
que havia sido provada com a fatoração dos vetores e a fórmula do seno da diferença.
O módulo do produto asterisco, ou do determinante, mede a área do paralelogramo
formado por A e B, se ||A|| for considerado o comprimento da base, ||B||senθ
corresponde à sua altura, e...
...a1b2 - a2b1 = ||A|| ||B|| senθ mede sua área:
... aliás quem mede a área de paralelogramos também mede a área de triângulos, o
triângulo com vértices P=(2,3), Q=(4,5) e R=(3,7) tem sua área igual à metade da área
do paralelogramo formado pelos vetores PQ=<2,2> e PR=<1,4>, ou seja,
(½) |PQ*PR| = (½) |(2)(4)-(2)(1)| = (½) 6 = 3.
Aliás, o produto asterisco a1b2-a2b1=||A||||B||senθ também pode ser um detetor de
alinhamentos, o produto apenas se anula se um dos vetores é nulo ou se o ângulo entre
eles é 0 ou 180º, casos de alinhamento ou oposição (alinhamento negativo), que são
resumidos pelo conceito de proporcionalidade de vetores. Assumindo que o vetor nulo é
proporcional a qualquer vetor, a1b2-a2b1=0 se e somente se A e B são proporcionais.
Aliás, com o produto asterisco obtemos fórmulas práticas para medir áreas cercadas por
poligonais, conta-se a lenda que um fazendeiro percorreu a fronteira poligonal de sua
fazenda, o "Rancho Tonyheart", situada lá perto de Paraibuna, acompanhado por seu
filho, o engenheiro Bob Golla:
(i) andou 44.721 metros a 63,43° a leste do norte, bem marcados por sua bússola
americana,
(ii) 28.284 metros no rumo noroeste,
(iii) 28.284 metros no rumo sudoeste,
(iv) 17.321 metros 26,56° a oeste do norte,
(v) 28.284 metros no rumo sudoeste,
(vi) finalmente 31.623 metros 56,31° a leste do sul, voltando ao seu ponto de partida.
Seu filho que o acompanhava de calculadora em punho, fixou um sistema de eixos, com
os eixos x e y apontando nas direções oeste-leste e norte-sul como usualmente se faz... e
a origem no ponto de partida. Então converteu os deslocamentos para a notação de
componentes,
... e a partir do seguinte diagrama,
... empregou o produto asterisco para calcular a área da propriedade, que correspondia à
área de quatro triângulos, com lados A1 e A2, A2 e A3, A3 e A4, A4 e A5, onde A1=<i>,
A2=A1+<ii>... e assim por diante... deixamos para o leitor o cálculo da área da fazenda.
Calculemos, também como exemplo, a área da região delimitada pela poligonal fechada
de vértices (0,0), (2,3), (1,5), (-2,4) e (-5,-3). Vamos desenhar a tal poligonal com o
programa mathematica,
... e vemos que a região pode ser dividida em três triângulos, cujos lados correspondem
aos vetores de posição R1=<2,3> e R2=<1,5>, R2 e R3=<-2,4>, R3 e R4=<-5,-3> ,
respectivamente.
Podemos calcular o produto estrela destes pares de vetores, obter as áreas dos triângulos
e somá-las, de novo com o mathematica...
levando-nos à área envolvida pela poligonal.
Por mais útil que a fórmula (I) nos seja, dá menos informação do que a fórmula (II),
notemos que no exercício acima, a direção de R1 é maior do que a de R2, a direção de
R2 é maior do que a de R3, a direção de R3 é maior do que a de R4 ...e pela fórmula (I)
os três produtos asteriscos calculados são positivos.
Isto ocorreu pela forma especial que nossa região tem, pode ser contornada por um
movimento cujos vetores de posição tem direção cada vez maior e o ângulo entre dois
deles não passa de 180°, mas o que ocorreria se a região tivesse a forma seguinte...
... vemos que ainda assim a área seria à metade da soma dos produtos asteriscos,
área = (½) {R1*R2 + R2*R3 + R3*R4}
... o sinal que aparece no segundo produto não nos atrapalha, mas ajuda!
O produto asterisco de vetores foi descoberto muito antes das matrizes e determinantes,
muito antes da regra de Cramer. Ao que parece, a origem da regra de Cramer está ligada
ao produto asterisco.
O autor E. Crowe, em "A History of Vector Analysis", hoje reeditado pela editora
Dover, comenta que o primeiro aparecimento que conhece da regra de Cramer ocorre
num artigo de Cauchy, estudando um sistema de duas equações e duas incógnitas com o
emprego do produto de Grassmann, ou asterisco.
Notamos que um sistema 2x2 típico, isto é o conjunto das duas equações escalares (1) e
(2) abaixo, onde x e y são incógnitas e as outras quantidades algébricas são dadas,
a1x + b1y = c1 (1),
a2x + b2y = c2 (2),
se tomamos A=a1i+a2j, B=b1i+b2j e C=c1i+c2j, o par de equações pode ser escrito como
uma única equação vetorial onde x e y são variáveis enquanto os três vetores são dados,
x A + y B = C (3),
assim o fez Cauchy em seu artigo, estudou a equação (3) vetorialmente, em vez de
trabalhar com o conjunto formado pelas equações (1) e (2).
Notem que o produto asterisco a1b2 - a2b1 = ||A|| ||B|| senθ entre A e B corresponde ao
determinante da matriz restrita de coeficientes do sistema
Somente no caso de proporcionalidade entre A e B, ou nulidade de um destes vetores,
este determinante dá zero, ou por ter duas linhas (ou colunas) proporcionais, ou por ter
uma linha (ou coluna) nula (notem que A e B são colunas da matriz, mas as conclusões
que tiramos sobre as linhas, também tiramos sobre as colunas, dadas as duas maneiras
possíveis de se definir o produto asterisco).
Notem que no caso de uma linha nula o sistema é possível indeterminado, pois temos de
fato apenas uma equação. No caso de duas linhas proporcionais temos duas equações
redundantes e novamente sistema possível indeterminado ou duas equações que se
contradizem e sistema impossível.
Então no caso de nulidade do produto asterisco de A e B o sistema é impossível ou
possível indeterminado, da equação (3) percebemos a diferença geométrica entre as
duas possibilidades, se A e B forem proporcionais e não nulos, o vetor C também tem
que ser proporcional a eles para que o sistema seja possível indeterminado. No caso de
um dos vetores ser nulo, o vetor C deve ser proporcional ao outro para que o sistema
seja possível indeterminado.
Quando o produto asterisco não é nulo, repetimos aqui as manipulações de Cauchy que
empregam as propriedades do produto asterisco e mostram que então o sistema é
possível e determinado, mais do que isto apresentam a solução na forma que hoje
chamamos regra de Cramer.
Faz-se então o produto asterisco dos dois lados da equação (3) pelo vetor A à esquerda,
emprega-se daí as propriedades do produto asterisco listadas na tabela acima para obterse:
A*(xA + yB) = A*C portanto x (A*A) + y (A*B) = A*C
e como (A*A) = 0, y = (A*C)/(A*B) (4)
...analogamente, fazendo o produto asterisco dos dois lados da equação por B à direita,
temos:
(xA + yB)*B = C*B portanto x ( A*B) + y (B*B) = C*B
e como (B*B) = 0, x = (C*B)/(A*B) (5)
notem que as equações (4) e (5) correspondem à regra de Cramer para a solução do
sistema quando este é possível e determinado.
Este artifício para resolver sistemas 2x2 com o produto asterisco, foi empregado pelo
matemático Cauchy quando os vetores começavam a ser descobertos, muito antes das
matrizes, dos determinantes e da regra de Cramer serem conhecidos.
13.2 A fórmula clássica com determinantes 3x3 encontradas em textos e apostilas de
EM, aplicações.
Consideremos um triângulo com vértices P=(xP,yP), Q=(xQ,yQ) e R=(xR,yR), podemos
associar dois deslocamentos aos lados deste triângulo, um que leva P em Q, o outro que
leva P em R. Tais deslocamentos correspondem à ação dos vetores A=(xQ-xP)i+(yQ-yP)j
e B=(xR-xP)i+(yR-yP)j.
Notemos então que:
e da igualdade entre (1) e (2) temos a opção de calcular um determinante 3x3 a partir
das coordenadas dos vértices do triângulo em vez de calcular uma matriz 2x2 a partir
das componentes dos vetores naturalmente associados aos lados do mesmo... talvez por
referir-se diretamente as coordenadas de vértices, talvez pela sua forma fácil de ser
lembrada, é a segunda forma a forma clássica nas apostilas e textos do EM.
A desvantagem de apresentá-la isoladamente, sem menção à sua relação com o produto
de Grassmann, é a de não ligar esta fórmula com a álgebra vetorial, mas até isto faz
sentido, como ressaltamos várias vezes, a Geometria Analítica que se ensina no nosso
EM é sem vetores.
Certamente, para apresentar-se a versão 2x2, ter-se-ia que introduzir o conceito de
vetor, ou ao menos de deslocamento.
Nos texto do EM e apostilas dos cursinhos aparece a fórmula A =(½) |D|, para a área do
triângulo com vértices P, Q e R, onde D é o determinante:
...fórmula muito útil nos vestibulares como vemos nos exemplos que seguem.
A demonstração desta fórmula pode ser feita diretamente, sem falar em vetores,
escolhendo bem um triângulo e colocando-o dentro de um retângulo,
...então a área do triângulo é igual à área do retângulo menos as áreas de três triângulos
retângulos:
A(retângulo) = (xQ - xP) (yR - yP) = xQ yR - xQ yP - xP yR + xP yP,
A(ΔP?Q) = (½) (xQ - xP) (yQ - yP) = (½) {xQ yQ - xQ yP - xP yQ + xP yP},
A(ΔQ?R) = (½) (xQ - xR) (yR - yQ) = (½) {xQ yR - xQ yQ - xR yR + xR yQ},
A(ΔR?P) = (½) (xR - xP) (yR - yP) = (½) {xR yR - xR yP - xP yR + xP yP},
...cancelam-se os fracos e do confronto, algo sobrevive dos fortes, para que obtenhamos:
A(ΔPQR) = (½) {(xR yP - xP yR) + (xQ yR - xR yQ) + (xP yQ - xQ yP)},
metade da expansão de Laplace do tal determinante 3x3 na terceira coluna (cheia de
uns),
e temos uma prova direta de que metade do determinante 3x3 é igual à área do triângulo
escolhido. Notem que, analogamente ao caso 2x2, trocando a ordem dos vértices, o
determinante pode trocar o sinal, mas a área não.
(226, p.72) -CESCEA- A distância do ponto (a,-b) à reta que passa pelos pontos (a,b) e
(-a,-b) é:
(A) |2ab|/√(a2+b2), (B) |2a|/√(a2+b2), (C) 2√(a2+b2), (D)|a+b|/√(a2+b2), (E) n.r.a. (para
escolher).
Comentários:
Aqui convém fazer alguns comentários. Existe uma fórmula que dá a distância de um
ponto P a uma reta que esteja descrita pela sua equação geral, assim uma opção seria
escrever a equação geral da reta e depois calcular a distância do ponto à reta pela tal
fórmula.
Entretanto, se a reta passa por dois pontos de coordenadas conhecidas, Q e R, como
neste caso, uma solução rápida é dividir a área do paralelogramo determinado por P, Q e
R pelo comprimento do segmento que liga Q e R,
O diagrama é auto-explicativo, basta dividirmos a área do paralelogramo pelo
comprimento do segmento QR para encontrar a distância procurada, façamos as contas
no mathematica,
(227, p.73) -GV- A área da figura hachurada no diagrama ao lado vale: (a)4.0, (b)3.5,
(c)3.0, (d)5.0, (e)4.5 (múltipla escolha).
Podemos efetuar a diferença entre as áreas de dois triângulos, um com vértices (0,1),
(4,0) e (4,4), outro com vértices (0,1), (4,0) e (3,2).
sendo (e) a opção correta.
Terminamos por notar que em vários textos de EM a equação de reta, dados dois
pontos, é escrita com o emprego do determinante 3x3, a idéia é a de que se os pontos
dados P=(xP,yP), Q=(xQ,yQ) pertencem a tal reta, um terceiro ponto, (x,y), para também
pertencer à reta, deve estar alinhado com os dois pontos dados, isto é, o triângulo
formado pelos três deve ter área zero, isto é:
12.3 Uma palavrinha sobre a lei dos senos e algumas de suas conseqüências.
A lei dos senos admite prova muito simples, seguimos aqui Coxeter em "Elementary
Geometry Revisited" onde o grande matemático parte da propriedade de que o ângulo
inscrito é metade do circunscrito.
Seja dado um triângulo ΔABC, com vértices A, B e C, lados a, b, c e ângulos α, β e γ,
ordenados da forma usual.
Desenhamos a circunferência circunscrita ao tal triângulo, então desenhamos o diâmetro
CJ e a corda JB desta circunferência.
Abaixo distinguimos os casos em que α é agudo e obtuso, respectivamente. Aparecem
os triângulos auxiliares ΔBJC e ΔCJB, que veremos, são triângulos retângulos.
No caso agudo, o ângulo oposto ao lado a do triângulo auxiliar que aparece coincide
com o ângulo α, pois estes dois ângulos são ângulos inscritos correspondentes ao
mesmo ângulo circunscrito, que é ∠ COB.
No caso obtuso, o ângulo φ, oposto ao lado a no triângulo auxiliar, é o suplemento de α,
visto que a soma do ângulo circunscrito correspondente a este com o ângulo circunscrito
correspondente àquele dá ∠ COB + ∠ BOC = 360°. No caso obtuso temos senφ = senα,
dada a igualdade dos senos de ângulos suplementares.
Tanto no caso obtuso quanto no caso agudo o triângulo inscrito é um triângulo
retângulo, pois o ângulo ∠ JBC é reto, dado que é ângulo inscrito oposto ao diâmetro,
associado ao ângulo circuncrito ∠ JOC = 180°.
Neste triângulo retângulo a hipotenusa é o diâmetro da circunferência circunscrita
enquanto que o lado a é oposto ao ângulo α no caso agudo e oposto ao ângulo φ = 180°
- α no obtuso.
Estas considerações levam-nos, nos dois casos, a:
senα = a / 2R ⇒ a / senα = 2R,
onde R é o raio da circunferência circunscrita.
Como poderíamos fazer construções análogas para β e γ, temos:
(a/senα) = (b/senβ) = (c/senγ) = 2R,
a esta Coxeter chama de lei dos senos estendida, que não apenas afirma a igualdade
entre os quocientes dos lados por seus ângulos opostos, mas também a igualdade de tais
quocientes com o diâmetro da circunferência circunscrita ao triângulo.
Reparem que para a lei dos senos não estendida, onde apenas afirmamos que os
quocientes dos lados pelos senos dos ângulos opostos são iguais entre si, pode-se fazer
uma prova muito mais rápida.
Para tanto basta lembrarmos que a área de um triângulo, como comentamos mais acima,
pode ser escrita como metade do produto de dois lados pelo seno do ângulo entre eles.
Calculando a tal área de três formas diferentes, obtemos a igualdade:
(½) ab senγ = (½) bc senα = (½) ca senβ,
dividindo estas igualdades por (½)abc temos a identidade entre os três quocientes.
A lei dos senos implica na fórmula para o seno da soma e portanto também na fórmula
para o seno da diferença (com alguns artifícios, também na fórmula para o cosseno da
soma e cosseno da diferença).
Para efetuar a prova, basta notarmos que em um triângulo qualquer ΔABC como o
acima, vale a relação:
a = b cosγ + c cosβ (*)
Notem que (*) corresponde a uma soma de projeções quando tanto β quanto γ são
agudos,
...porém é uma diferença de projeções quando um destes ângulos é obtuso (notemos, na
figura da direita, em que β é obtuso, como a propriedade cos(180°-β) = - cosβ, relação
conhecida entre ângulos suplementares, garante (*) mesmo neste caso).
Partindo de (*), basta substituirmos nesta fórmula as relações:
a = 2R senα,
b = 2R senβ,
c = 2R senγ,
todas decorrentes da lei dos senos, para obter:
2R senα = 2R senβ cosγ + 2R senγ cosβ,
dado que α + β + γ = 180°, senα = sen(180°-(β+γ)) = sen(β+ γ) (novamente
empregamos a igualdade entre os senos de ângulos suplementares). Substituindo esta
relação e cancelando o termo comum 2R na fórmula mais acima obtemos a fórmula para
o seno da soma:
sen(β+ γ) = senβ cosγ + senγ cosβ.
Terminamos por notar que a área de um triângulo pode ser escrita como A=(½)absenγ,
empregando a lei dos senos, senγ=c/2R e obtemos que A=abc/4R. A área é metade do
quociente entre o produto dos lados e diâmetro da circunferência circunscrita.
Também é conhecida a fórmula que dá a área como metade do produto da soma dos
lados pelo raio da circunferência inscrita no triângulo, ou como mais se prefere dizer, o
produto do semi-perímetro pelo raio da circunferência inscrita,
...para tanto o diagrama acima é auto-explicativo.