Aula 3 Tutoria GASL

Tutoria de GASL – Aula 3
Produto escalar, norma e projeção ortogonal
Exercícios a serem resolvidos:
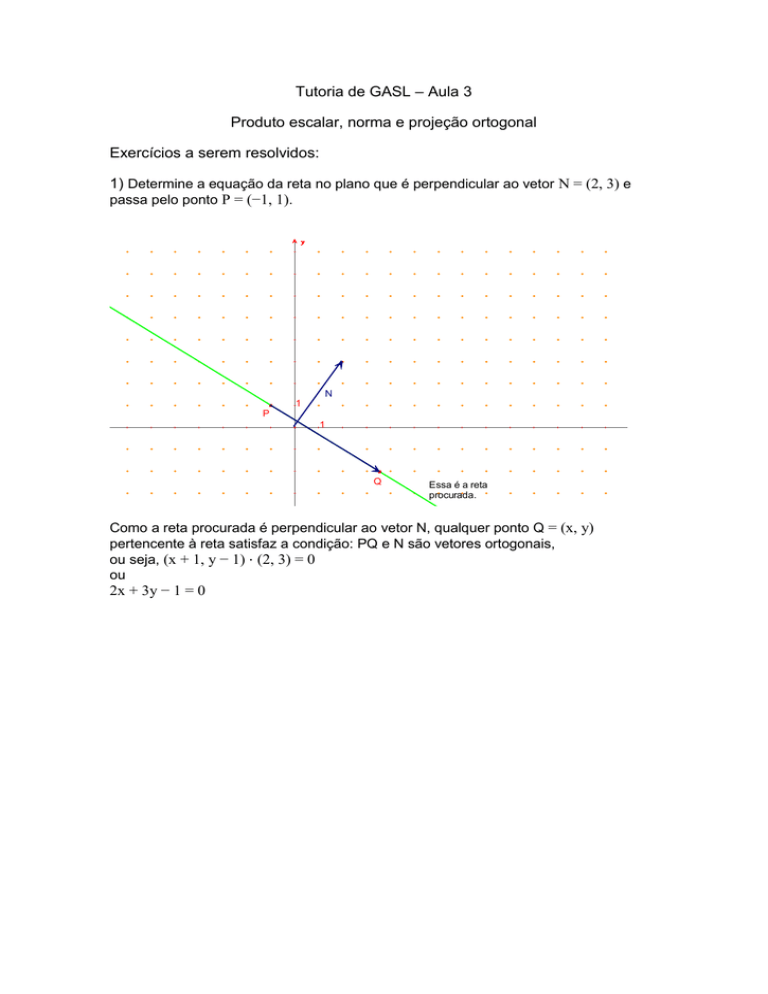
1) Determine a equação da reta no plano que é perpendicular ao vetor N = (2, 3) e
passa pelo ponto P = (−1, 1).
N
1
P
1
Q
Essa é a reta
procurada.
Como a reta procurada é perpendicular ao vetor N, qualquer ponto Q = (x, y)
pertencente à reta satisfaz a condição: PQ e N são vetores ortogonais,
ou seja, (x + 1, y − 1) ⋅ (2, 3) = 0
ou
2x + 3y − 1 = 0
2) Seja O = (0, 0). Qual o lugar geométrico dos pontos P = (x, y) tais que
∣∣OP∣∣2 = 4? Que equação algébrica representa esse lugar? E se O = (0, 0, 0) e
P = (x, y, z)? Qual a equação nesse caso?
Inicialmente interpretar o problema no plano:
Procurar que os alunos pensem na figura antes de desenhá-la na lousa. Sendo
P = (x, y), deduzir da sentença ∣∣OP∣∣2 = 4 a equação da circunferência x2 + y2 =
4.
Analogamente para a esfera de centro na origem e raio 2.
3) Sejam V =⃗i + 2⃗j − 3⃗k e W = 2⃗i +⃗j − 2⃗k. Determine vetores unitários paralelos
ao vetor V +W
V+W =
3i 3j5k,
seja S o vetor procurado. Então S = (3b, 3b, -5b) e
9b2 + 9b2 + 25 b2 = 1. b = 
S
2
= 1.
1
. ...
43
4) Ache o ângulo entre os seguintes pares de vetores:
U = 3⃗i + 3⃗j e V = 2⃗i +⃗j − 2⃗k
Considere a relação entre o cosseno do ângulo α entre os vetores U e V e o produto
UV
escalar entre eles: cos α = U . V .
U
= 3 2,
V
= 3 , U  V = 9, então cos α =

2
, α = 4 rad.
2
5) Decomponha W = −⃗i − 3⃗j + 2⃗k como a soma de dois vetores W1 e W2, com W1
paralelo ao vetor S = ⃗j + 3⃗k e W2 ortogonal a este último.
W
W2
S
W1
W1 = projS W =
WS
S
2
S
= (0, 3/10, 9/10)
e W2 = W - W1 = (-1, -33/10, 11/10).
6) Mostre que A = (3, 0, 2), B = (4, 3, 0) e C = (8, 1,−1) são vértices de um triângulo
retângulo. Em qual dos vértices está o ângulo reto?
A
C
B
Considerando os vetores AB = (1, 3, -2); AC = (5, 1 -3) e BC = (4, -2, -1), calculamos o
produtos escalar dois a dois, que leva ao seguinte resultado: AB•BC = 0. Concluímos
que os vetores AB e BC são ortogonais e portanto o ângulo reto tem vértice em B.
Observações: Ao propor o exercício, deixar que os alunos pensem sobre por alguns
minutos antes de resolvê-lo. Se possível pedir que algum aluno faça sua resolução na
lousa. Se houver tempo pode-se apresentar mais de uma solução para o mesmo
exercício.