Lançamentos. - Stoa Social

Resumo de Aula:
Lançamentos.
Quadro 1:
Equações do MUV.
• Função da posição
at 2
s = s0 + v0 t +
2
• Função da
velocidade
v = v 0 + at
• Equação de
Torricelli
v 2 = v 02 + 2a∆s
• Regra de Merton
∆s v 0 + v
=
2
∆t
Quadro 2: O valor de
“g” .
O valor da aceleração
média gravidade na
Terra é de 9,87 m/s2.
Mas este valor pode
variar de acordo com
a altitude e longitude
do local.
Na
maioria
dos
problemas
teóricos
apresentados
arredondamos o valor de g
para 10m/s2 para
simplificar os cálculos
1- Introdução
O estudo dos lançamentos é uma aplicação do estudo
do Movimento Uniforme e do Movimento
Uniformemente Variado. Todas as equações utilizadas
serão as destes movimentos.
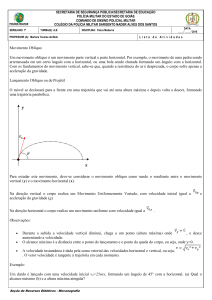
A maior diferença é que estaremos tratando de
movimentos verticais, além dos horizontais. Para
podermos descrever adequadamente este movimento
Figura 1
utilizamos o plano xy (Figura 1) para orientarmos o
movimento.
Apesar de este sistema poder ser utilizado em qualquer situação, vamos,
para simplificar alguns problemas, adotar o eixo vertical sendo positivo para
baixo. Isto não faz diferença nenhuma para a física, pois estas orientações
espaciais são arbitrárias.
2- Queda livre
A queda livre é o estudo da queda dos corpos sob ação exclusiva da
gravidade. Apesar de na prática isto não ocorrer de verdade1 (pois há sempre a
resistência do ar), existem muitos casos onde o movimento pode ser
aproximado por uma queda livre2.
Figura 2
Quando um corpo é abandonado em queda livre
ele possui aceleração constante g, e sua análise faz
uso das equações do MUV. A diferença é a escolha da
orientação do movimento. Neste caso a escolha mais
simples é orientar o sinal de positivo para baixo.
Nesta escolha tanto as velocidades quanto a
aceleração serão positivas (pois apontam no mesmo
sentido da orientação). O zero da trajetória é colocado
no ponto onde o corpo é abandonado (veja a Figura
2).
O valor de g normalmente é dado. Por simplificação é adotado, em geral, o
valor de 10m/s2 (veja Quadro 2).
3- Lançamento Vertical
Figura 3
Neste lançamento um corpo é disparado com
uma velocidade inicial v0 na vertical para cima
(Figura 3). A velocidade diminui por ação da
gravidade até que o corpo pare no ponto mais alto
da trajetória (v = 0). Em seguida ele começa a cair
atingindo novamente o solo no ponto onde ele foi
lançado.
Se aplicarmos a equação de Torricelli na
solução do problema podemos calcular o valor da
altura h atingida em função da velocidade inicial.
Observe:
1
2
Exceto no caso de experimentos controlados.
Como no caso de corpos aerodinâmicos caindo de pequenas alturas.
1
www.plantaofisica.blogspot.com
Quadro 3:
Trigonometria.
Considere um triângulo retângulo como o
da figura a seguir.
Define-se o seno do
ângulo α como:
senα =
Esta altura é a mesma que será percorrida na queda, apenas devemos trocar
o sinal. Então, usando novamente Torricelli.
v 0 = 0

v 02
v 02

2
2
2
v = v 0 + 2a∆s ∆s = −
⇒ v = 0 + 2g
⇒ v 2 = v 02
2g
2g

a = −g
Ou seja, a velocidade com que o corpo retorna ao solo é, em módulo, a
mesma com que ele partiu. Como conseqüência disto o tempo de subida será
igual ao tempo de descida, e o tempo de permanência no ar (tempo de voo) será
o dobro deste valor.
c.o.
hip
Define-se o co-seno do
ângulo α como:
cosα =
v = 0
v2

v 2 = v 02 + 2a∆s ∆s = h ⇒ 0 = v 02 − 2gh ⇒ h = 0
2g
a = −g

c.a.
hip
t↑ = t↓
e
t voo = 2t ↑
4- Lançamento horizontal
Neste caso lançamos um objeto na direção horizontal de um ponto situado a
uma altura h do solo, como alguém chutando uma bola do topo de um prédio.
Após o lançamento o objeto mantém sua velocidade horizontal inicial v0x, mas
passa a acelerar para baixo devido à ação da gravidade. Com resultado disto o
corpo descreve uma trajetória parabólica como mostrada na Figura 4.
O lançamento horizontal é um exemplo de composição de movimentos.
Temos um MU na direção horizontal e um MUV na direção vertical. Os dois
movimentos estão conectados pelo tempo. O tempo que o objeto leva para
atingir o chão é o tempo que ele se move na horizontal (o que nos permite
calcular o alcance).
Figura 4
5- Projeção de vetores
Antes de avançarmos precisamos aprender
uma técnica conhecida com projeção de
vetores. Considere inicialmente um vetor
r
v que faz um ângulo α com a horizontal.
Podemos escrever este vetor como a soma
de dois vetores perpendiculares entre si. Um
vetor na direção do eixo x que chamaremos de
r
v x e outro na direção do eixo y, chamado
Figura 5
2
www.plantaofisica.blogspot.com
r
de v y (observe a Figura 5).
Se utilizarmos a trigonometria (veja quadro 3) podemos escrever:
senα =
cosα =
r
vx
v
vy
v
⇒ v x = v.senα
⇒ v y = v.cosα
r
Os vetores v x e v y são chamados de projeções (ou componentes) do vetor
r
v . Na prática é muito mais fácil lidar com as projeções de um vetor do que o
vetor em si.
6- Lançamento Obliquo.
No lançamento obliquo o corpo é lançado com velocidade v0 com um
ângulo a com a horizontal. O movimento descrito pelo corpo é um arco de
parábola como o mostrado na Figura 6.
Figura 6
Para a analisar o movimento nós o decompomos em dois movimentos: um
no eixo x e outro y (Figura 7), determinando as componentes da velocidade
nestes eixos como mostrado no item 5.
Figura 7
No movimento horizontal temos um MU, pois, desprezando a resistência do
ar, não há aceleração nesta direção. Como conseqüência disto a velocidade
neste eixo será sempre v0x, inclusive no ponto mais alto da trajetória. Já na
direção y o movimento resume-se a um lançamento vertical. Como no caso do
lançamento horizontal os dois movimentos podem ser relacionados pelo tempo:
o tempo que o corpo demora para subir até o ponto mais alto e descer até o nível
do solo é o tempo que ele se move da direção horizontal (que determinará o
alcance)
É possível demonstrar que lançamentos com ângulos complementares
possuem o mesmo alcance e que o ângulo de 45º fornece o alcance máximo.
Veja mais sobre Física e Matemática no Site
Plantão de Física - ΠΦ
www.plantaofisica.blogspot.com
3