QUESTAO_UERJ_1fatima log

Interbits – SuperPro ® Web
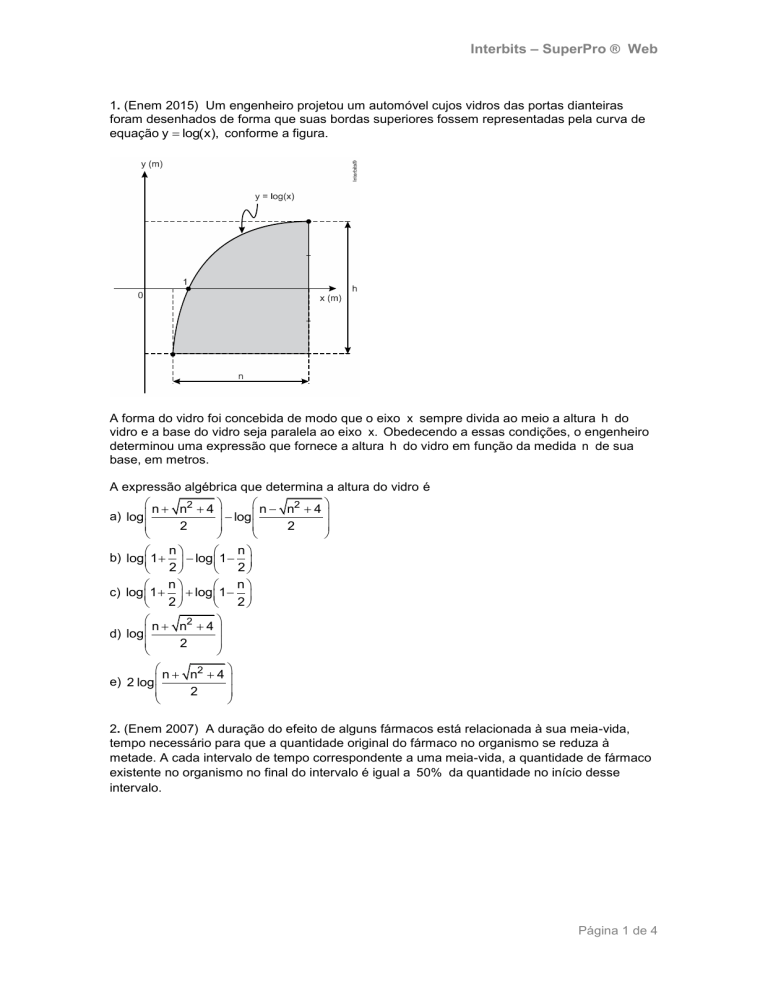
1. (Enem 2015) Um engenheiro projetou um automóvel cujos vidros das portas dianteiras
foram desenhados de forma que suas bordas superiores fossem representadas pela curva de
equação y  log(x), conforme a figura.
A forma do vidro foi concebida de modo que o eixo x sempre divida ao meio a altura h do
vidro e a base do vidro seja paralela ao eixo x. Obedecendo a essas condições, o engenheiro
determinou uma expressão que fornece a altura h do vidro em função da medida n de sua
base, em metros.
A expressão algébrica que determina a altura do vidro é
 n  n2  4 

2

  log  n  n  4 
a) log 




2
2




 n
 n
b) log  1    log  1  
 2
 2
 n
 n
c) log  1    log  1  
 2
 2
 n  n2  4 

d) log 


2


 n  n2  4 

e) 2 log 


2


2. (Enem 2007) A duração do efeito de alguns fármacos está relacionada à sua meia-vida,
tempo necessário para que a quantidade original do fármaco no organismo se reduza à
metade. A cada intervalo de tempo correspondente a uma meia-vida, a quantidade de fármaco
existente no organismo no final do intervalo é igual a 50% da quantidade no início desse
intervalo.
Página 1 de 4
Interbits – SuperPro ® Web
O gráfico anterior representa, de forma genérica, o que acontece com a quantidade de
fármaco no organismo humano ao longo do tempo.
F. D. Fuchs e Cher l. Wannma. Farmacologia Clínica.
Rio de Janeiro: Guanabara Koogan,1992, p. 40.
A meia-vida do antibiótico amoxicilina é de 1 hora. Assim, se uma dose desse antibiótico for
injetada às 12 h em um paciente, o percentual dessa dose que restará em seu organismo às
13 h 30min será aproximadamente de
a)
b)
c)
d)
e)
10%.
15%.
25%.
35%.
50%.
Página 2 de 4
Interbits – SuperPro ® Web
Gabarito:
Resposta da questão 1:
[E]
h
Seja k, com 0  k  1, a abscissa do ponto para o qual se tem logk   , ou seja,
2
h
h  2  logk. Assim, temos  log(n  k), isto é, h  2  log(n  k). Daí, vem
2
2  log(n  k)  2  logk  log(n  k)  k  log1
 k 2  nk  1  0
k 
n  n2  4
.
2
Portanto, temos
h  2  log(n  k)

n  n2  4 
 2  log  n 


2


 n  n2  4 
.
 2  log 


2


Resposta da questão 2:
[D]
De 12 h às 13 h 30min temos 1,5 meias-vidas. Assim, do gráfico podemos concluir que às
13 h 30min o percentual da dose que restará no organismo é aproximadamente 35%.
Página 3 de 4
Interbits – SuperPro ® Web
Resumo das questões selecionadas nesta atividade
Data de elaboração:
Nome do arquivo:
28/02/2016 às 19:16
UERJ 1
Legenda:
Q/Prova = número da questão na prova
Q/DB = número da questão no banco de dados do SuperPro®
Q/prova Q/DB
Grau/Dif.
Matéria
Fonte
Tipo
1 ............. 149394 ..... Elevada ......... Matemática ... Enem/2015........................... Múltipla escolha
2 ............. 75517 ....... Média ............ Matemática ... Enem/2007........................... Múltipla escolha
Página 4 de 4