uniandrade – faculdades alvorada

UNIANDRADE – FACULDADES ALVORADA
1ª LISTA DE EXERCÍCIOS DE ÁLGEBRA LINEAR
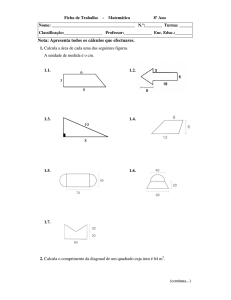
SISTEMA DE INFORMAÇÃO
PROFª CLAUDIA C. DA ROSA
01) Construa cada uma das matrizes indicadas abaixo:
 
b) B  b 
c) C  c 
a) A  aij
2x 3
, tal que aij  2i  j
ij 3x 4
, tal que bij  i 2  j
ij 3x 3
, tal que cij  i  j 3  2
 i  j , se...i  j
,
tal
que
d


ij
4x 2
2i  3 j , se...i  j
 
d) D  d ij
 i, se.....i  j
 0, se.....i  j
e) E  eij 5x 2 , tal que eij   2
 j  2, se....i  j

 
02) Encontre a matriz transposta de cada matriz do exercício 01.
03) Determine os números reais x e y em cada caso:
3  10 3
x  1
a) 

x  y   1 2
 1
3 x  2 y  8 1 
 8
b) 

5  4 5
x  3y
04) Dadas as matrizes M e N e sabendo que M  N t , determine o valor de x e de y:
x 2
M 
x
y
 e
2 y
x
N 
2 y
x2 
.
y
 2
x2 
05) Seja A  
 . Sabendo que A é uma matriz simétrica encontre o valor de
2 x  1 0 
x.
  1
1 2 3 
 2 0 1
06) Considere as matrizes: A  
, B
, C=  2  , D  2  1 .


2 1  1
 3 0 1
 4 
Faça as operações indicadas quando possível e justifique caso não for possível.
a) A + B
b) A . B
c) B . C
d) C . D
e) D . A
f) D . B
g) –A
h) –D
i) 2.A + 3.B
j) B – 4.A
07) Coloque verdadeiro ou falso. Justifique as verdadeiras e dê um contra exemplo para
as falsas.
a) (
) A matriz nula é a única triangular superior e triangular inferior ao mesmo
tempo.
b) (
) Todos os elementos da diagonal principal de uma anti – simétrica devem ser
nulos.
c) (
) Toda matriz identidade é uma matriz diagonal.
d) (
) Se A é uma matriz qualquer então ( At ) t  A
e) (
) Se A é uma matriz diagonal então At  A
f) (
) Se At  A então A é uma matriz diagonal.
g) (
) A é simétrica  At  A .
h) (
) Dadas duas matrizes A e B de mesma ordem temos que:
A  B 
2
 A 2  2. A.B  B 2
“Somente no dicionário que o sucesso vem antes do trabalho”.