FREQUÊNCIA COMPLEXA

FREQUÊNCIA COMPLEXA
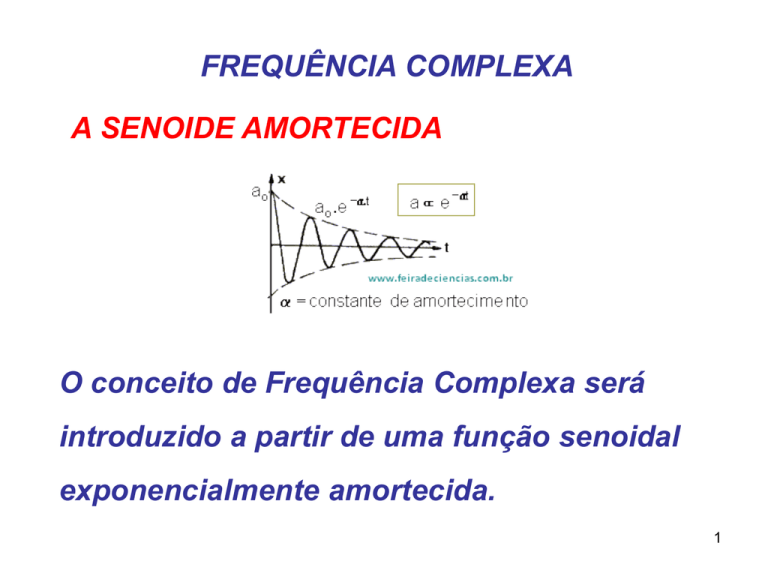
A SENOIDE AMORTECIDA
O conceito de Frequência Complexa será
introduzido a partir de uma função senoidal
exponencialmente amortecida.
1
FREQUÊNCIA COMPLEXA
A TENSÃO SENOIDAL AMORTECIDA
É a tensão da forma
v(t) = VM e t cos( t +  ),
em que α é real negativo.
Se   0 e   0  v(t) = VM cos(  ) = V0 ,
(constante)
Se   0 e   0  v(t) = VM cos(  )e t  V0e t , (exponencial)
Se   0 e   0  v(t) = VM cos( t +  ),
(senoidal)
Note que o expoente de e, ou seja, αt, é adimensional. Assim, por
exemplo, em e
-3t
as dimensões de -3t são Nepers (Np) e -3 é a
frequência neperiana em Np/s.
2
FREQUÊNCIA COMPLEXA
st
Uma função do tipo f(t) = K e , em que K e s são
constantes complexas, é caracterizada pela
frequência complexa s, sendo s    j.
Para uma tensão constante, pode-se escrever
v(t) = V0 e0t , ou seja, s  0.
Para uma tensão na forma exponencial,
tem-se que v(t) = V0 e t , ou seja, s    j 0.
3
FREQUÊNCIA COMPLEXA
Para uma tensão senoidal v(t) = VM cos( t +  ),
é preciso escrever a função cosseno na forma
exponencial.
Da identidade de Euler, tem-se que e j  cos + jsen
Somando-se estas duas
expressões, tem-se que:
O que resulta em:
e-j  cos - jsen
e j + e-j  2 cos
cos 
1 j
e + e-j 
2
Assim, tem-se que:
cos( t +  ) 
1 j( t+ ) -j( t+ )
e

+e
2
4
FREQUÊNCIA COMPLEXA
Substituindo-se esta expressão em
v(t) = VM cos( t +  ),
tem-se que:
1 j( t+ )
e
+ e-j( t+ ) 
2
1

1

v(t) =  VM e j  e jt   VM e  j  e  jt
2

2

v(t) = VM
1

Fazendo, K1   VM e j 
2

Obtém-se
e
1

K 2   VM e  j 
2

v(t) = K1 e jt  K 2 e jt
Observe também que
K1 e K2 são complexos
conjugados.
Observa-se então, que a tensão senoidal é caracterizada por um par de
frequências complexas conjugadas
s1  j
e
s2   j .
5
FREQUÊNCIA COMPLEXA
Para a tensão senoidal exponencialmente amortecida
v(t) = VM e t cos( t +  ),
tem-se que:
1 j( t+ ) -j( t+ )
e

+e
2
1

1

v(t) =  VM e j  e(   j )t   VM e j  e(   j )t
2

2

v(t) = VM e t
v(t) = K1 e(   j )t  K 2 e(   j )t
A tensão senoidal exponencialmente amortecida é
caracterizada também por um par de frequências complexas
conjugadas
s1    j e s2    j .
6
FREQUÊNCIA COMPLEXA
Observe que a senoide exponencialmente amortecida é o caso
geral, quando nem α nem ω são nulos.
A tensão constante, a exponencial e a senoidal são vistos como
casos particulares da senoide exponencialmente amortecida .
Devemos ser capazes, agora, de reconhecer por inspeção as
frequências complexas associadas a essas tensões.
Exemplos:
v (t )  100
s 0
v (t )  5e2t
s  2
v (t )  2sen(377t )
s1  j 377 e s2   j 377
v (t )  4e 3t cos(6t  30o )
s1  3  j 6 e s2  3  j 6
7
FREQUÊNCIA COMPLEXA
Consideremos agora o caso inverso, ou seja, dada uma
frequência complexa ou um par conjugado de frequências
complexas, devemos ser capazes de identificar a natureza da
função a que estão associadas.
Se s=0, temos uma constante e K é real;
Um valor positivo de s, como s=5, identifica uma função
exponencialmente crescente, Ke5t, em que K deve ser real para
que a função seja física.
Um valor negativo de s, como s=-5, refere-se a uma função
exponencialmente decrescente, Ke-5t, (K também deve ser real).
Um valor de s puramente imaginário, como por exemplo, s=j2,
nunca pode ser associado a uma quantidade real, porque a forma
Kej2t resulta em K(cos2t+jsen2t).
8
FREQUÊNCIA COMPLEXA
Para se construir uma função real é necessário considerar valores
conjugados de s, como s1= j2 e s2= -j2, que devem ser associados
a valores conjugados de K. Neste caso, tem-se uma tensão
senoidal com frequência angular de 2 rad/s. Se conhecermos K,
podemos construir a função senoidal.
Por exemplo, se K1= 6 + j8 e K2 = 6 - j8, obtém-se a senoide real
V(t) = 20 cos(2 t + 53,13°). (Façam a transformação).
De maneira análoga, um valor geral de s, como s = -3 + j5, somente
pode ser associado a uma quantidade real se estiver acompanhado
de seu conjugado s = -3 - j5. Neste caso, tem-se uma senoide
exponencialmente decrescente Ae-3tcos(5t+θ). A amplitude e o
ângulo de fase vão depender dos valores específicos de K1 e K2.
Se K1 = 4+j3 e K2 =4-j3, tem-se a exponencial decrescente:
V(t) = 10e-3tcos(5 t + 36,87°). (Façam a transformação).
9
FREQUÊNCIA COMPLEXA
OUTRA INTERPRETAÇÃO DA FREQUÊNCIA COMPLEXA
O conceito padrão de frequência traz também outro significado
além de “repetições por segundo”. O valor da frequência está
relacionado também à velocidade de mudança da função
considerada.
Alta frequência significa variação rápida. Este significado também
pode ser abstraído da frequência complexa de uma função
exponencial complexa no tempo.
Seja f(t) = Kest . A taxa de variação de f(t) é df(t)/dt = sKest.
Normalizando, dividindo por f(t), tem-se que:
df(t)/dt
sKest

s
st
f(t)
Ke
10
FREQUÊNCIA COMPLEXA
OUTRA INTERPRETAÇÃO DA FREQUÊNCIA COMPLEXA
Ou seja, essa taxa de variação normalizada é uma constante
independente do tempo e é identicamente igual à frequência s.
Assim, podemos também interpretar a frequência complexa como a
taxa normalizada de variação no tempo da função exponencial
complexa.
11
FREQUÊNCIA COMPLEXA
EXERCÍCIO
Três resistores são conectados a um capacitor com energia inicial
armazenada. A forma de onda de tensão Vc é exibida em um
osciloscópio. Para t=30ms, Vc=50V e decresce a uma velocidade
de 1000V/s. Determine os instantes de tempo em que:
a) Vc=25V;
Resp. 64,7ms.
b) A taxa de mudança de Vc é -100V/s.
Resp. 145ms
12