PC1-S6

MODELANDO SISTEMAS LTI
NO DOMÍNIO DA
FREQUÊNCIA.
PC - Semana6
1
MODELANDO SISTEMAS LTI NO
DOMINIO DA FREQUÊNCIA



Podemos trabalhar com a modelagem de qualquer
tamanho de sistema LTI através de equações
diferencias.
Porem, o uso desta técnica torna os cálculos
complicados e trabalhosos para equações diferencias
de alta ordem ou modelos de estado de muitas
variáveis.
Por isso não deduzimos ainda expressões para o sinal
de saída de sistemas LTI utilizando equações
diferenciais.
PC - Semana6
2
MODELANDO SISTEMAS LTI NO
DOMINIO DA FREQUÊNCIA




A caracterização de um sinal pelas freqüências das
oscilações separadas tem vantagens, não somente para
músicos, mas também por razões técnicas.
Muitos sistemas são conhecidos por produzir um sinal de
saída senoidal se um sinal de entrada senoidal é
introduzido.
A fase e a amplitude do sinal de saída pode ter mudado
em relação à entrada, mas a freqüência permanece a
mesma.
Veremos que os sistemas LTI possuem exatamente esta
propriedade.
PC - Semana6
3
MODELANDO SISTEMAS LTI NO
DOMINIO DA FREQUÊNCIA



Em geral, o efeito sobre a fase e a amplitude são
diferentes para cada freqüência, e o
conhecimento desta efeito para todas as
freqüências ajuda a modelar sistemas.
Este tipo de modelo é chamado modelo no
domínio da freqüência e é freqüentemente mais
simples de tratar que um modelo no domínio do
tempo.
O Sistema é LTI no domínio da frequência.
PC - Semana6
4
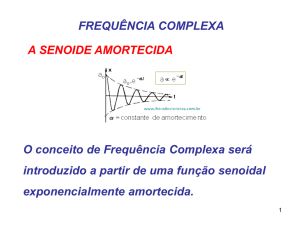
X̂
Freqüência Complexa





O que é uma Freqüência Complexa?
A tradicional definição é derivada dos valores
reais de um sinal y(t) senoidal.
Tal sinal é caracterizado por uma amplitude X e
o numero de oscilações por unidade de tempo f,
e pela passagem do valor zero em relação ao
instante t = 0.
A freqüência f é um numero real.
Junto com a fase real φ ele descreve exatamente
a posição de todos os cruzamentos de zero:
PC - Semana6
5
Freqüência Complexa
x(t )  Xsen(2ft   )
(3.1)
Estendendo o conceito para um valor
complexo, temos:
x(t )  Xe
Onde
st
(3.2)
s    j
PC - Semana6
6
Xˆ  1  j
Freqüência Complexa


Em contraste à eq.
3.1, somente o
tempo t é real. A
amplitude X e a
freqüência s são
complexos.
A figura seguinte
mostra um exemplo
de sinal exponencial
complexo com :
PC - Semana6
Xˆ  1  j
7
Exemplo de sinal exponencial complexo
•Para t=0, x(t)=X
•Para t>0, x(t) é definido pela
parte real e imaginaria de s.
PC - Semana6

x(t )  Xˆ et

  2f
8
Exemplo de sinal exponencial complexo




Ele é definido para todos os
pontos no tempo, mas é
somente mostrado aqui
para t  0.
Para t = 0, x(t) pega o
valor da amplitude
complexa X.
E para t  0, x(t) é definido
pela parte real (σ) e
imaginária (ω) de s.
A parte real é conhecida
como o modulo de x(t),
PC - Semana6
9
Exemplo de sinal exponencial complexo


Enquanto a parte imaginária corresponde à
freqüência angular ω=2f, e indica o quão
rapidamente o sinal complexo da figura
anterior orbita em torno do eixo do tempo.
O relacionamento com oscilações reais pode
ser visto pela separação das partes real e
imaginária de x(t), como na próxima figura.
PC - Semana6
10
Exemplo de sinal exponencial complexo
PC - Semana6
11
Frequência Complexa: Exemplo de Sinais

Como exemplo do uso de freqüências
complexas, nós apresentamos alguns
sinais reais por função exponencial
complexa na tabela do slide seguinte.

PC - Semana6
12
Sinais de Exemplo.
Sen()=1/2j x (e
j
-e
– j )
e
cos()=1/2j x (e j  + e –j )
PC - Semana6
13
Frequência Complexa : Exemplo de sinais





Para X  R e para valores reais de s, x(t) é real.
No caso mais simples, se s é igual a zero e X=1, então
x(t) é igual a 1 e o sinal torna-se constante.
Um sinal exponencial real é obtido para outros valores
reais de s, por exemplo, x(t) = e-3t para s=-3.
Os sinais senoidais com valores reais podem ser
representados superpondo-se duas funções
exponenciais complexas com freqüências puramente
imaginarias s=jω e s=-jω .
Superpondo funções exponenciais com σ  0 leva ao
decaimento (se σ < 0) ou crescimento (se σ  0 ) de
oscilações senoidais.
PC - Semana6
14
Plano de Frequência Complexa




A vantagem da freqüência complexa é que muitos
tipos de sinais podem ser expressos por um único
parâmetro de freqüência complexa.
Para dar uma idéia, às formas diferentes de função
exponencial complexa podem ser designados os
valores correspondentes num plano de números
Gaussianos.
Ele é chamado de freqüências complexas ou plano-
s.
O slide seguinte mostra as funções exponenciais
complexas para posições diferentes no plano de
freqüências complexa.
PC - Semana6
15
Plano de Freqüência Complexa.
PC - Semana6
16
Plano de Frequência Complexa





O distanciamento do eixo real torna a
oscilação mais rápida.
Olhando na direção do eixo do tempo, na
metade do plano positivo acima, onde é
positivo, a oscilação complexa segue no
sentido horário e na parte de baixo ela
segue no sentido anti-horário.
No eixo real, o sinal não oscila.
Formas de sinal na metade direita do plano
crescem mais rapidamente se elas estão
mais afastadas do eixo imaginário.
Enquanto formas de sinal na metade
esquerda do plano decaem.
PC - Semana6
17
O que são Eigenfunctions?




Em geral não existe grande similaridade entre o
comportamento no tempo entre sinais de entrada e
saída de um sistema.
Existem sistemas, por outro lado, que permite a
certos sinais de entrada atravessarem o sistema
sem sofrer mudança em seu comportamento no
tempo.
Por exemplo: redes elétricas constituídas somente
de resistências, capacitores e indutores.
Sua resposta a um sinal senoidal é usualmente
(para componentes lineares) outro sinal senoidal,
com somente a amplitude e a fase sendo
diferentes.
PC - Semana6
18
O que são Eigenfunctions?






Funções seno e cosseno podem ser colocadas juntas em
funções exponenciais.
E então as mudanças de amplitude e fase podem ser
expressas por um único fator: a amplitude complexa.
O sinal de saída pode então ser obtido do sinal de entrada
pela multiplicação de um fator complexo.
Um fenômeno similar é conhecido da álgebra
linear: para certos vetores x, o produto de x com a
matriz A é igual a um múltiplo do vetor x: Ax=x.
Então x é chamado eigenvector e  é chamado
eigenvalue.
Nós usamos esta notação também para sinais que
passam através de um sistema sem mudar sua
forma.
PC - Semana6
19
Eigen Functions.

Um sinal e(t) que quando entra num
sistema, produz na saída a resposta
y(t)=  e(t) com a constante
complexa  , é chamado a
eigenfunction deste sistema.
PC - Semana6
20
Trabalhando um sistema com
eigenfunction a(t)
PC - Semana6
21
Eigenfunctions de sistemas LTI.

Quando um sinal senoidal atravessa
redes lineares sem mudar sua forma,
e pode também ser representado por
funções exponenciais complexas.
y (t )  x(t )


Podemos demonstrar que
.
Para provar
nossa teoria começamos
st
x(t )  e
com um sinal de entrada da forma
PC - Semana6
22
Eigenfunctions de sistemas LTI.



E procuramos a resposta correspondente do
sistema y(t) que podemos escrever como uma
função do sinal de entrada: y(t) = S{x(t)}
A seguir nós usamos as propriedades de
sistemas LTI: a não variação de tempo e a
linearidade.
Nós começamos com a resposta de um sinal de
entrada mudado no tempo
x(t   )  e
s ( t  )
PC - Semana6
23

E por causa da invariança no tempo nós obtemos:

y(t   )  S x(t   )  S e

s ( t  )
 Se
 s
e
st

O fator e-s não depende do tempo. Por causa da
linearidade segue ainda que:


 
y(t   )  S e s e st  e s S e st  e s y(t )

Agora embora nós não tenhamos y(t), nós temos uma
equação de diferença para y(t) que é:
y(t   )  e

 s
y(t )  .e
st
.
PC - Semana6
24







Então temos que
é uma
x(t )  e st
eigenfunction do sistema LTI descrita por s.
A constante  identifica o comportamento de s.
Como linearidade e invariância ao tempo foram
somente as pré-condições, nós não podemos
afirmar mais nada sobre .
Em geral,  depende da freqüência complexa s.
Nós escrevemos, portanto, =H(s).
E chamamos H(s) a função do sistema ou função
de transferência, pois ela descreve o sistema e suas
propriedades de transferência da entrada para a
saída.
A conexão com o modelo do sistema no domínio do
tempo será vista adiante.
PC - Semana6
25
Relação entre eigenfunction e FT de um
sistema LTI.
PC - Semana6
26